And better yet, lightning fast system testing. It's 4:00 JST, and I would've woken up a lot more to see if I passed systests.

when comparing x,y,z,w, we can determine which are the smallest and largest, and determine the difference (more important). If the difference is d, than there can be only (n-d) variations for x,y,z,w

I found an interesting solution that scales easily to bigger problems:

long long n,a,b,c,d,x;
cin >> n >> a >> b >> c >> d;
f.push_back(a+b);
f.push_back(a+c);
f.push_back(b+d);
f.push_back(c+d);
sort(f.begin(), f.end());
x = f[3] - f[0];
cout << n * max(0ll, n - x);

We want to calculate distance from i to j. If j < a[i] then distance is 1. Otherways, it is optimal to move to cell with maximal a[i] (to maximize our range at next step). That is, distance[i][j] = distance[m][j] + 1, where m is cell with maximal a[i].

He said "Also we can solve this problem in O(1)." So above was O(n) solution, but it could be done for O(1).

The O(1) solution is mentioned but not actually given. You can use the following formula, n·(max(0, n - max(a + b, a + c, c + d, b + d) + min(a + b, a + c, c + d, b + d))). Proof is left as an exercise to the reader, of course. B-)

http://codeforces.net/contest/675/submission/17953232

Fixed, thanks

You're correct

The first submission is not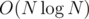 , since it is naive BST and hence might get unbalanced to have O(N) height  = O(N²) performance over N insertions.

Example case: 15 0 0 0 -15
The prefix sum: 15 15 15 15 0
As you can see, the answer is 1 since 15 occur 4 times
The repeated prefix sum means there are 4 part which produce zero (in case 15)

Let i is the array position where 0<=i<5
The first part is i=0 and i=4 -> we directly move the money from i = 0 to i = 4 since zero sum is guaranteed.
The second part is i = 1 -> 0 move
The third part is i = 2 -> 0 move
The fourth part is i = 3 -> 0 move

So the answer is 1.
Conclusion number of repeated prefix sum means number of parts if the sum of subarray from 0 to x is the repeated prefix sum.

You have 3 different explanations from above :) Ask clarifying questions to one of those comments.

Suppose that the money is as follows ----> -1 2 -3 5 3 -6

Then the prefix sums will be -----> -1 1 -2 3 6 0

Since the highest frequency is 1 so our k=1 and answer = N-1

Another Example be ------> 15 -5 5 -15

Prefix Sums ---> 15 10 15 0

15 is repeated twice so answer = 4-2 = 2 transfers one from 15 to -15 and 5 to -5

A segment of x bank accounts which sums to zero needs x-1 money transfers to make all bank account money =0 .

For eg:- 5 0 -5

i)  First we transfer 5 from first bank account to second bank account. Now accounts look like this

           0 5 -5

 ii)  Then we transfer -5 from second bank account to third bank account. Now accounts look like this :- 

           0  0  0

Thus is 2 ( 3-1 ) transfers I made all account's money to zero.

Now suppose there are k segments in given array whose sum is equal to zero. Let length of segments be x1,x2,....,xk .

Now for first segment we take x1-1 transfers , for second x2-1 .... and for kth xk-1 transfers.

Total number of transfers = x1-1+...... xk-1 = (x1+x2+x3+....xk)- (1+1+...ktimes) = n — k

If we want to minimize total number of transfers we have to maximize value of k( Remember we assumed number of segments to be k )

So what can we do to maximize value of k ?

Let f[1],f[2],f[3],....f[n] denote cumulative sums of given array.

f[i] = a[1] + a[2] +.... a[i]

f[j] = a[1] + a[2] + ..... a[j]

Suppose f[i]=f[j] then

a[1] + a[2] +.... a[i] = a[1] + a[2] +....  a[i] + a[i+1] + .... a[j]

 Therefore , a[i+1] + a[i+2] +..... a[j] =0 

 Also since the sum of array as a whole is given to be zero .

             Remaining array sum is also zero.

      a[j+1] + a[j+2] .... a[1] + a[2] + .... a[i] =0

Therefore we got 2 segments with sum =0 when we had two cumulative sums same.

Now suppose f[i] = f[j] = f[k] for some 1<=i,j,k <=n , i<j<k

a[1]+a[2] + ....  a[i] = a[1]+a[2] +....a[i] + a[i+1] + ... a[j] 

 a[1]+a[2]+ ....  a[j] = a[1]+a[2] +....a[j]+a[j+1]+... a[k]

Therefore a[i+1]+....a[j]=0 a[j+1]+....a[k]=0 a[k+1]+....a[1]+...a[i]=0

Therefore we got three segments with sum=0 , when we got 3 cumulative sums whose values were same .

Therefore try to find the frequency of most frequent cumulative sum and reduce it from n to get answer.

Hope it helps.

hope my explaination helps.. ;)

See this

Obviously the answer is less than the number of banks, which shows that when you put all these banks on a ring and use some roads to connect these banks, there are at least one road where no money goes through in the optimal way.

Let's cut one road, break the ring into a list and iterate all the banks. It is easy to see that whenever the prefix sum becomes zero, we can find a way to transfer money in the banks we have iterated so we can cut the next road.

Now we just need to iterate the road we cut at first and maintain all prefix sums. Every time we fix the current road and cut the next road, all prefix sums would simultaneously increase or decrease by a number, which depends on the order you iterate, so we just need to maintain the offset.

note that center '?' can be in range 1~n, whatever other '?' is.

I don't know how this works in your computer but one of the problems is here :

if(it==my.end()){
  ans = (*(it--)).f;
  (*(it--)).s.s = true; 
}

when it==my.end() , then it isn't element, so haven't .first ! if you used -- for going back before using it, you must write it like this --it.

also notice that in every place you used it--, it's value is really changed and isn't temporary.

There is only 10^5 * 10^5 different correct positions, because every position can be set by two numbers

Your algorithm has problems when the input is a decreasing array. It has nothing to do with the speed difference between C# and C++.

You code a solution that's O(n) for every insertion. Test it locally with:

100000
1 2 3 4 ...

The tree generated with this has a form like a list: 1 -> 2 -> 3 -> ...

So, for every insertion you transverse all the tree, since, O(n)

nice one.... I like the approach

This solution might lead to unbalanced BST. This leads to O(N) height and O(N^2) insertions.

Sorry if my explanation is tedious.

Let's consider the second example: 4 2 3 1 6

At first, our BST is empty, so the root value will be 4. That means that all values that lie in the interval [1, 3] will go to the root's left, and all values that lie in the interval [4, 10^9] will go to its right.

So, at the moment we have two candidate places to put our next number: [1, 3] (value=4) and [5, 10^9]{value=4}.

If we insert the next value we find that it should to go the root's left because 2 is in [1,3]. Since we have filled the root's left children, we must remove the interval [1, 3]{value=4} and add two new ones: [1, 1]{value=2} and [3,4]{value=2}. So now we have the following candidates: [1, 1]{value=2}, [3,4]{value=2} and [5, 10^9]{value=4}.

If we do the same thing with all sequence values we will know all parent values and we will keep an updated information about where new values should go. It is not necessary to keep the empty intervals (i.e: those that its right value is smaller than its left), since that means that no value can be a child of that node.

In order to know quickly on what interval a new value should go you can keep them sorted by its right values, then for a number x find the first interval right that it is greater or equal than x. You can do this because you know the interval is unique (as the BST paths are).

You can check my solution for more clarification: http://codeforces.net/contest/675/submission/18001556

It was just more comfortable for me to use 0-based indexing. You can use 1-based indexing if you want.

Yes, I know that editorial for E is too short, sorry about that.

ρ_i, j = 1 for j = i + 1... m

ρ_i, j = ρ_m, j = 1 for j = m + 1... a_i

ρ_i, j = 1 + ρ_m, j for j = a_i + 1... n - 1

Sum of ρ_i, j for j = m + 1... n - 1 equals to dp_m + n - 1 - a_i

Sum of ρ_i, j for j = i + 1... m equals to m - i

So, sum of ρ_i, j for j = i + 1... n - 1 equals to dp_i = (dp_m + n - 1 - a_i) + (m - i) = dp_m - (a_i - m) + n - 1 - i

Hope, those comments will be useful for you: first, second

Your formula is a bit wrong. But even if it was right I don't understand why it's . If we calculate dp naively we get O(n²) solution. Also we can keep dp_m + m in segment tree and find maximum in what leads to solution.