Hey!
Polish Collegiate Team Programming Contest (AMPPZ 2016) took place today, organized by University of Wroclaw. This is my first ACM experience, and I want to share with you my impressions.
To begin with, I'm still a high schooler (2nd grade). However, thanks to generosity of UWroclaw organizers team and some charity institutions, a few best high school teams were able to participate.
Now let's talk about the contest. My teammates were Paweł Burzyński(pawelek1) and Kacper Kluk (wonrzrzeczny). None of us is a really fast coder, so we just decided to focus more on accuracy than speed. As we'll see later, this was kind of a good idea.
The contest started with no delays. I was not expected to be the coding monkey, but somehow it happened that three first and easiest tasks were accepted by me. These were not really challenging, so let's just ignore this fact. Some time later, Kacper scored the "ifologic" problem C. Then, the difficulty has risen.
Meanwhile, teams of UWarsaw1 and 2 were skyrocketing, grabbing quite outstanding scores of 7 problems per 90 minutes and 9 problems after the first half of the contest. After 2,5 hours there were 2 problems with no solves. The problemset was rather on the technical side and at this stage it was only a matter of time who will manage to implement more tasks correctly. As for our team, Paweł scored an interesting F and Kacper was implementing G. B was still unsolved, but we were giving it a try, because it looked like a problem which requires just careful cases handling for which probably most top teams had no time.
There were still two number theory problems left, two graphs, two implementations G and (super awful) B and a something-with-convex-hull-problem E. At that point we had an accuracy of 0 incorrect tries, which gave us a good position even though our solving times was average. Paweł got into E and Kacper finished G, and at 3:15 we had 7 (+20 penalty).
After this, we got quite stuck on harder problems. Because we couldn't solve anything harder, I was chosen to code some clever backtracking for B. A similar problem was already on AMPPZ 2014, named pillars (http://main.edu.pl/en/archive/amppz/2014/fil). While I was adding new and new ideas to the solution, other guys were thinking on EIHL. 30 minutes left, and Paweł sat to code his I solution. Unsurprisingly, it had some bugs. There was little time left, so we had to speed up. We were working together, but I barely knew what the solution should do. We debugged the samples and... WA. 10 minutes before the end, we still had WA and Paweł had basically no ideas what could be wrong. I still don't know how I came up blindly with the right idea, but three mintues later we were happy with the AC. 8 problems with 2 incorrect tries during the whole competition -> that was rather well. At that point we knew we were going to be top10, and we were really satisfied.
After the contest, we had some time to discuss the problems with friends and meet some famous people. We've even managed to have a picture taken with Petr! :)

Then, the solutions presentation and final ceremony took place. The organizers prepared amazing piece of work which simulated the ranking in a really cool way. The final results :
UWarsaw1 (mnbvmar, Marcin_smu, Swistakk) 11.
*Google (Petr, Franken, Kwasnicki) 10.
UWroclaw2 (Lowicki, Syposz, Michalak) 9.
UWarsaw3 (znirzej, tabasz, tribute_to_Ukraine_2022) 8.
*III High School Gdynia (kpw29, pawelek1, wonrzrzeczny) 8.
- means unofficial participation. I'll post the official data (statements, results) as soon as they're published. Right now, you can enjoy live ranking from the first 4 hours of contest at : http://solve.edu.pl/~amppz/chartcode2016/ranking.html.
Our results were really satisfactory. And what about you? How was your first ever ACM contest? I'm not talking about such programming legends as [Bredor] and his http://codeforces.net/blog/entry/45106 ACM story, just average people. I'm writing this mostly for myself to remember this event, but I will appreciate any answers :)
One more thing. I want to thank the organizers for an interesting problemset and a reaaaally cool event. Thank you, and thank all people who contributed to it. Looking forward to seeing you in @amppz2017!











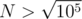 answer is
answer is 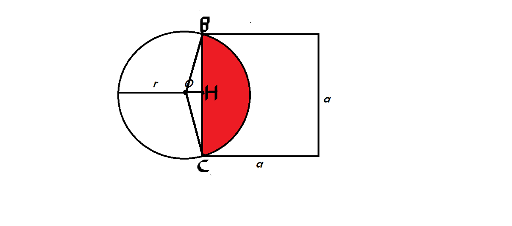

 . We name
. We name 
 =
= 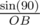
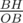
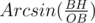
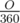 *
* 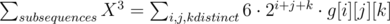 + similar terms for
+ similar terms for 
