Блог пользователя natalia

Онлайн-курс на Stepik
Автор natalia, история, 5 лет назад, По-русски

Дорогие посетители Codeforces!

Наступают летние каникулы — лучшее время для подготовки к олимпиадам. Именно поэтому мы запускаем для вас курс Спортивное программирование на платформе Stepik! Преподаватели курса: Наталья Бондаренко (natalia) – золотой призер ACM ICPC 2009 года и серебряный призер 2010 года, Андрей Гайдель (Shlakoblock) и Елена Рогачева (elena) – тренеры команд Самарского университета и организаторы олимпиад по спортивному программированию.

Старт курса — 1 июля, но записываться можно уже сейчас. Особо нетерпеливые могут пройти этот курс на платформе Coursera, на которой он уже запущен.

В процессе работы с двумя платформами, мы видим большое преимущество Stepik в том, что на нем каждое задание представляет собой отдельный шаг. После успешной сдачи или нескольких неудачных попыток по заданию, слушатель получает возможность обсуждать решение с другими слушателями и преподавателями, публиковать свое правильное или неправильное решение независимо от ситуации с другими заданиями. Наш предыдущий курс Математика для олимпиад по программированию породил огромное количество таких обсуждений. Мы надеемся, что новый курс окажется не менее интересным и полезным для участников. Он включает в себя много практики решения задач.

С уважением, команда курса.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +48
  • Проголосовать: не нравится

Онлайн-курс "Спортивное программирование"
Автор natalia, 6 лет назад, По-русски

Дорогие посетители Codeforces!

На платформе Coursera запущен онлайн-курс Спортивное программирование! Авторы курса: Наталья Бондаренко (natalia) – золотой призер ACM ICPC 2009 года и серебряный призер 2010 года, Андрей Гайдель (Shlakoblock) и Елена Рогачева (elena) – тренеры команд Самарского университета и организаторы олимпиад по спортивному программированию.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +49
  • Проголосовать: не нравится

Онлайн-курс "Математика для олимпиад по программированию" — запуск 2
Автор natalia, история, 7 лет назад, По-русски

Дорогие посетители Codeforces!

На платформе Stepik планируется повторный запуск курса Самарского университета Математика для олимпиад по программированию. Курс откроется 22 мая.

Первый запуск, как мы считаем, прошел довольно успешно. Мы получили много ценных отзывов и комментариев от наших слушателей, и сейчас курс закрыт на доработку. Какие изменения вас ждут после запуска:

  • Ко всем задачам проверочных тестов добавлены правильные решения.
  • Добавлены 35 дополнительных задач повышенной сложности, которые будут интересны в том числе и тем, кто уже прошел курс в первый раз.
  • Курс будет запущен без дедлайнов, и это означает, что его можно будет проходить в удобном для себя темпе (тем более, что нас ждут экзамены/лето/...).
  • В связи с добавлением новых задач и снятием дедлайнов, будут немного повышены пороги для получения сертификата, что сделает его получение еще более интересным и почетным.

Идея этого курса возникла благодаря студенческим математическим кружкам, которые я вела в Саратовском и Самарском университетах. Курс строится на решении и разборе математических задач по темам, полезным для начинающего спортивного программиста:

  1. Комбинаторика.
  2. Теория чисел.
  3. Геометрия.
  4. Инварианты и полуинварианты.
  5. Теория игр.

По своему уровню курс рассчитан на Div 2 и новичков, но, возможно, некоторые задачи поставят в тупик и более опытных участников. Все успешно завершившие курс получат сертификаты Самарского университета.

В общем, записывайтесь на курс, будет интересно!

Полный текст и комментарии »

  • Проголосовать: нравится
  • +74
  • Проголосовать: не нравится

Чему учат в ЦОППе?
Автор natalia, история, 8 лет назад, По-русски

Добрый день!

Сегодня я наконец-то решила опубликовать мою статью, посвященную Центру олимпиадной подготовки имени Н.Л. Андреевой. Это структурное подразделение Саратовского государственного университета, ведущее подготовку студентов к соревнованиям по программированию.

Я занималась в ЦОППе все 5 лет моей учебы. После этого 6 лет преподавала в СГУ, при этом продолжала поддерживать связь с ЦОППом, помогала проводить олимпиады и тренировки. Этой статьей я хочу подвести некоторый итог моей деятельности, связанной с ЦОППом, и выразить бесконечную благодарность его прекрасному коллективу. К моей благодарности присоединяется Polichka, которая помогала с редактированием. Я попытаюсь ответить на следующие вопросы:

Чему полезному для будущей профессии можно научиться в ЦОППе? Какую роль ЦОПП играет в университетском образовании?

Надеюсь, и сообществу Codeforces, и людям, не связанным с олимпиадным программированием, будет интересно. Статья была написана во время моего преподавания в СГУ, в ней много сравнений студентов ЦОППа с обычными студентами, приходящими ко мне на пары.

Пару слов о том, как организован тренировочный процесс в ЦОППе. Прийти в ЦОПП может любой желающий студент СГУ. В основном занимаются студенты КНиИТа и мех-мата, всего 30-40 человек. Для них организуются личные и командные контесты, а также лекции — отдельно для нового набора, отдельно для студентов, тренирующихся больше одного года. Два контеста + одна лекция — это 12 часов в неделю. Довольно приличная нагрузка, даже если не считать время на дорешивание и выполнение домашнего задания к лекциям, которое заключается в решении задач в архив. Многие не справляются и уходят в течение первого года. Наиболее сильные студенты, ориентированные на результаты в международный соревнованиях, занимаются еще больше. Участвуют в раундах Codeforces и их подготовке, ездят на олимпиады и сборы, ходят на математический кружок. Летом проходят личные тренировки (конец июня — начало июля), сборы в Сазанке (начало августа) и, наконец, в конце августа школа в летнем лагере, в которой участвуют все студенты ЦОППа и где формируются команды на четвертьфинал.

На что эти ребята тратят свое время и что они получат в результате, кроме олимпиадных дипломов? Чему их научат в ЦОППе?

Попытаюсь ответить по пунктам.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +194
  • Проголосовать: не нравится

Программа абитура по информатике
Автор natalia, 10 лет назад, По-русски

Как-то решила полюбопытствовать, чему учат в школе в Германии. Думаю, вам тоже будет интересно.

Абитур (Abitur) — это экзамен, который сдают немецкие школьники при окончании гимназии для поступления в университет. Вкратце о системе образования в Германии. После окончания 4-летней начальной школы дети в зависимости от их способностей и желания родителей распределяются по трем типам школ: 9-летней общеобразовательной школой (Hauptschule), 10-летней средней школой (Realschule) и 12-летней гимназией (Gymnasium). Сроки обучения указаны в сумме с начальной школой. Поступать в университет можно только после гимназии. В последние два года обучения в гимназии школьники обладают достаточно большой свободой в выборе предметов, которые будут учить и сдавать. Предметы можно изучать на базовом или продвинутом уровне. Поэтому приведенная ниже программа абитура относится только к наиболее способным школьникам (оказавшимся в гимназии, а не в школе другого типа) и при этом планирующим поступать на специальность, связанную с IT.

Тематически обучение в последние два года гимназии уже выходит за рамки нашей школьной программы и скорее соответствует первым курсам вуза. Например, абитур по математике состоит из трех больших блоков: дифференциальное и интегральное исчисление, теория вероятностей и аналитическая геометрия. Насчет информатики судите сами.

Абитур может проходить в разных гимназиях и в разных землях (Bundesländer) Германии по-разному, хотя многие земли проводят централизованный абитур, особенно по основным предметам. Так что скорее всего программа не является единственной существующей.

Программа абитура

I. Объектно-ориентированное программирование

I1. Концепция объектно-ориентированного программирования

  • классы, объекты, атрибуты, методы, инкапсуляция
  • диаграммы классов (проектирование, имплементация)
  • отношения между классами: ассоциация, наследование
  • абстрактные классы, полиморфизм

I2. Структуры данных

  • Линейные структуры данных
    • Очередь и стек
      • применение стандартных операций
      • реализация стандартных операций
    • Линейные списки
      • применение стандартных операций
    • Алгоритмы поиска и сортировки
      • рекурсия
      • поиск
      • сортировка вставками
      • на продвинутом уровне: QuickSort
  • Деревья
    • Бинарное дерево
      • применение стандартных операций
      • алгоритм обхода
    • Бинарное дерево поиска
      • применение стандартных операций
      • алгоритм обхода
      • на продвинутом уровне: реализация методов insert и search
  • Только на продвинутом уровне: графы
    • матрица смежности, списки смежности
    • применение стандартных операций
    • обход графа в ширину и в глубину
    • поиск кратчайшего пути между вершинами: перебор, алгоритм Дейкстры

I3. Проектирование сетевых приложений

  • сетевые протоколы, TCP/IP
  • клиентские приложения
  • клиент-серверные приложения
  • криптография
    • симметричное шифрование (Цезарь, Виженер)
    • асимметричное шифрование (RSA)
    • обмен ключами (Диффи-Хеллман)

II. Реляционные базы данных

  • моделирование жизненных задач при помощи модели сущность-связь
  • схемы баз данных
  • нормализация: приведение баз данных к первой и третьей нормальным формам
  • реляционная алгебра (выбор, проекция, объединение, разность, декартово произведение, переименование)
  • SQL-запросы к одной или нескольким таблицам
  • аспекты защиты данных

III. Конечные автоматы и формальные языки

  • моделирование жизненных задач при помощи конечных детерминированных автоматов
  • представление конечных детерминированных автоматов графами и таблицами
  • формальные языки: регулярные языки и их грамматики
  • на продвинутом уровне: разработка парсера для одного простого формального языка

Заранее прошу меня простить за качество перевода. Мое знание немецкого языка, да и (чего там греха таить) некоторых пунктов программы далеко от совершенства. Но вроде бы удалось сохранить смысл. Буду рада исправлениям и уточнениям, вот оригинал. Как я поняла из пояснений оттуда, разделы I1 и I2 обязательны, из остальных трех пунктов I3, II и III в школе должны пройти хотя бы два. Наиболее распространенные языки программирования — Delphi и Java.

И на закуску задача с экзамена. Задача взята вот отсюда. Это немного другой вариант абитура, из другой земли. Последняя задача, продвинутый уровень, одна из сложных.

  • Выбирается число 2 ≤ z ≤ 6. Берется некоторая перестановка чисел от 1 до z. Это ключ.

  • Перестановка записывается в верхнюю строчку таблицы, слева направо.

  • Имеется некоторый текст (строчка из латинских букв). Он записывается слева направо под перестановкой. Когда строка таблицы заканчивается — переходим на следующую.

  • Если последняя строчка заполнена не до конца — добавляются символы #.

  • После этого цифры перестановки переставляются в порядке возрастания вместе с соответствующими столбцами.

  • Выписывая содержимое таблицы в естественном порядке, получаем зашифрованный текст.

Дан текст aidsttssegrneeghm#i# и ключ 3 1 4 2.

Опишите алгоритм расшифровки текста.

Приведите расшифрованный текст.

Приведите алгоритм перебора всех перестановок из n элементов для заданного числа n ≥ 2.

Напишите программу, которая делает следующее:

  • Читает текст.

  • Выбирает число z, 2 ≤ z ≤ 6, при помощи генератора случайных чисел.

  • Перебирает все перестановки чисел от 1 до z.

  • Выбирает одну перестановку при помощи генератора случайных чисел.

  • Шифрует текст.

  • Выводит зашифрованный текст.

Используйте в программе ваш алгоритм для перебора всех перестановок чисел от 1 до n.

Напишите программу, которая делает следующее:

  • Читает зашифрованный текст и соответствующую перестановку.

  • Дешифрует его.

  • Выводит расшифрованный текст.

Протестируйте программы друг с другом. Опишите тестирование ваших программ.

Опишите методы разработки, которые вы использовали.

Мне в этой задаче весьма нетривиальным кажется перебор всех перестановок. До него не додумаешься, если не проходили хотя бы что-то аналогичное. Хотя задача состоит из нескольких пунктов и легко набрать частичные баллы.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +52
  • Проголосовать: не нравится

Олимпиады на www.i-olymp.ru
Автор natalia, 11 лет назад, По-русски

Дорогие посетители Codeforces!

Возможно вы уже слышали про Открытые международные студенческие Интернет-олимпиады на http://www.i-olymp.ru/, о которых я узнала только вчера. Олимпиады проводятся по самым разнообразным дисциплинам. Согласно официальному сайту, это довольно представительные соревнования. В них участвуют МГУ, СПбГУ, Новосибирский ГУ, Самарский ГАУ и многие другие вузы России и ближнего зарубежья. Немного настораживает прайс-лист.

Кто-нибудь из вас участвовал раньше в этих соревнованиях? Если да, интересно было бы узнать впечатления. В первую очередь интересуют дисциплины "Математика" и "Информатика". Как вы оцениваете уровень задач, участников и организации? Какие призы? Кто составляет задачи? Стоит ли участие в этих олимпиадах запрашиваемых денег? :)

UPD. Спасибо большое всем отписавшимся. Получается, что олимпиада по математике не такая уж и плохая, хотя и с кучей организационных проблем. Про информатику непонятно, потому что, по всей видимости, это не контест :)

Полный текст и комментарии »

  • Проголосовать: нравится
  • +12
  • Проголосовать: не нравится

Об Открытом Кубке и его онсайтах
Автор natalia, 12 лет назад, По-русски

Доброго времени суток, дорогие посетители Codeforces!

Сегодня в Петрозаводске прошел Onsite Round XII Открытого Кубка имени Е.В. Панкратьева.

За почти 9 (!) лет своего существования, Открытый Кубок стал одним из самых популярных соревнований по программированию в России и странах СНГ. Высокий уровень соревнования создает очень суровая конкуренция. Пройти в онсайт Открытого Кубка сложнее, чем в финал ACM ICPC (это не относится только к некоторым московским и питерским командам, у которых очень высокая конкуренция для выхода в финал внутри вуза). Отсутствие ограничений на возраст и удобная схема проведения сделали Открытый Кубок излюбленным соревнованием для многих ветеранов ACM ICPC. В нем участвуют практически все русскоязычные лидеры рейтингов Topcoder и Codeforces. Мне по странному стечению обстоятельств еще школьницей довелось поучаствовать в самом первом экспериментальном раунде в мае 2004 года. С тех пор я регулярно пишу Кубок в разных составах, и мне небезразлична его дальнейшая судьба.

Конечно, за историю существования Открытого Кубка было немало багов в задачах и тестах, ошибок тестирующей системы, падений серверов, читерства со стороны участников, неожиданных изменений в правилах, нерейтинговых раундов. Будем надеяться, многое из перечисленного навсегда осталось в прошлом. Организаторы уверенно справляются с проблемами, находят новых спонсоров и проводят смелые эксперименты. Открытый Кубок продолжает расширять географию и с каждым годом становится все более и более престижным соревнованием.

Надеюсь, я не очень утомила вас длинным введением. Перехожу собственно к проблеме. Сегодняшний онсайт произвел на меня совершенно демотивирующее воздействие. Авторы в принципе не скрывают, что задачи были взяты с Japanese Alumni Group Contest 2, прошедшего в апреле 2012 года. С помощью гугла по условиям задач быстро находится сайт http://acm-icpc.aitea.net, с которого можно скачать тесты. Один из участников моей команды — Коля Кузнецов (NALP) — прорешивал этот контест ранее, когда готовился к финалу 2012 года. Этот контест есть у нас на одном из саратовских тренировочных сайтов. Задача F, как оказалось, вообще была на контесте в Петрозаводске вчера! Когда Дима Матов (Nerevar) увидел вчера эту задачу, он вспомнил, откуда она, и напомнил про этот контест нашим командам в Петрозаводске. Не исключено, что другие участники онсайта тоже ранее сталкивались с этими задачами. Аналогичная ситуация была и на прошлом онсайте. Задачи гуглились, по ним можно было скачать тесты и даже засабмитить решения в online-judge.

Несмотря на честность участников, мне в этом видится большая проблема. Кто-то мог видеть задачи и помнить решения. Проведение онсайта на уже использовавшемся ранее комплекте задач не соответствует уровню Открытого Кубка. Раунды регулярного сезона как правило авторские и готовятся на приличном уровне, почему нельзя так же подготовить и онсайт?

Организаторы объясняют ситуацию тем, что в Открытом Кубке все хотят участвовать, поэтому никто не может готовить задачи. К тому же, в уже апробированных задачах гораздо меньше вероятность ошибок в условиях и тестах. Но ведь не все авторы задач — крутые участники. Я верю, что если приложить определенные усилия, можно найти авторов, не прошедших в онсайт и способных подготовить качественный комплект задач за определенную плату. Даже если плата небольшая — соревнование очень престижное. На твоих задачах будут сражаться Petr с Egor-ом против tourist-а за звание победителей Открытого Кубка! Одна неверная попытка может перечеркнуть все их усилия в отборочных этапах за полгода!

Даже если подготовка оригинальных задач нереальна и приходится брать задача из источников, можно хотя бы использовать источники, которых нет в открытом доступе. Например, переводить задачи с национальных школьный олимпиад, которые недоступны на английском языке, или комбинировать разные источники. Что я хочу предложить в любом случае — это перед следующим онсайтом собрать экспертную комиссию, которая смогла просмотреть уже готовый комплект и оценить его "баянистость". Желательно, чтобы это были географически распределенные представители из основных центров спортивного программирования, скорее всего тренеры или опытные участники, которые следят за задачами официальных соревнований и тренировок. Потому что даже если задачи будут новыми, не исключено их совпадение с чем-то хорошо известным. Задачи могут быть, например, незнакомы питерцам, но хорошо известны саратовцам по одной из последних тренировок. По моему мнению, чтобы обеспечить оригинальность и адекватность комплекта задач онсайта уровню участников, его должна оценивать группа экспертов, по численности и по уровню сопоставимая с жюри хорошего четвертьфинала. И очень хочется, чтобы это были новые, оригинальные задачи.

Надеюсь, что мне не одной ситуация видится в таком свете и мой пост поможет выработать общее конструктивное решение проблемы.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +140
  • Проголосовать: не нравится

Ищу команду для участия в Открытом Кубке
Автор natalia, 13 лет назад, По-русски

Всем добрый день!

В связи с неожиданными изменениями в расписании Кубка я остаюсь без команды, так как Дима Матов (Nerevar) на выходные меня покидает. Поэтому было бы очень здорово объединиться с кем-нибудь еще, у кого в команде не хватает человека.

Моя цель — пройти на онсайт. Поэтому главное условие — преемственность нашей сборной с Saratov SU Retired либо с вашей командой (если у нее высокий результат в настоящий момент) и мое участие в онсайте, если пройдем. Еще крайне желательно, чтобы вы могли взять меня на все три этапа (6, 7 и 9 мая). Расписание есть на сайте www.opencup.ru.

Ваше географическое положение особой роли не играет. Надеюсь, в связи со сложными обстоятельствами разрешат участвовать дистанционно.

Если есть деловые предложения — пишите в личку, а вот троллить, наоборот, лучше где-нибудь в другом месте.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +39
  • Проголосовать: не нравится

C Днем защитника Отечества!
Автор natalia, 13 лет назад, По-русски

Удивительно, что все как-то подзабыли, что сегодня, 23 февраля, в России праздник — День защитника Отечества. Поздравляю с этим замечательным праздником представителей сильной половины человечества от лица другой половины, менее многочисленной на Codeforces. Дорогие мужчины, вы у нас самые умные, обаятельные, изобретательные и веселые. Счастья, здоровья, успехов, великих свершений, удачи на контестах и побед на всех фронтах!

выложить фото без регистрации

Полный текст и комментарии »

  • Проголосовать: нравится
  • +134
  • Проголосовать: не нравится

Codeforces Round #100: разбор задач
Автор natalia, 13 лет назад, По-русски

Задача А. Новогодний стол

Тарелки должны касаться края стола, а значит, их центры должны лежать на окружности радиуса R - r (см. рисунок). 

В случае если тарелки имеют наибольший возможный радиус для данного стола, их центры будут располагаться в вершинах правильного n-угольника, вписанного в эту окружность. Задача сводится к тому, чтобы найти длину стороны вписанного правильного n-угольника и сравнить ее с 2r. Формулу для длины стороны a = 2(R - r)sin (π / n) нетрудно вывести. Для этого нужно рассмотреть прямоугольный треугольник, нарисованный зеленым цветом.

При реализации нужно было аккуратно выделять случай, когда выполняется равенство r = (R - r)sin(π / n) (*). Из-за вычислительной погрешности правая часть может получиться больше левой, что приведет к ответу "NO" вместо "YES". Сравнение в таких случаях нужно проводить с участием маленького ε: 
a + ε < b вместо a < b ,
a < b + ε вместо a ≤ b.
Константу ε нужно выбирать таким образом, чтобы она была меньше возможной разности между точными значениями a и b, если они не равны. В частности, при вычислениях по формуле (*) с учетом ограничений задачи эта разница может составить примерно 7· 10 - 7. Поэтому ε   = 10 - 7 достаточно, а ε  = 10 - 6 - уже нет. 

В очередной раз акцентирую внимание на том, что выбор ε  зависит от конкретных формул, по которым происходят вычисления и сравнения. Разные решения могут проходить и не проходить с одним и тем же ε .

Задача носила чисто реализационный характер. Заметим, что номер отправленной открытки однозначно определяется номером друга и множеством открыток, имеющихся у Александра в данный момент. Разберем пример из условия. 
  12 3 4 
 {1} -1 1 1 
 {1, 2}21 11 
 {3, 1, 2}3 3 1 3 
 {3, 1, 2, 4}33 1 3 
Первый столбец таблицы содержит множества открыток, получающиеся у Александра после получения каждой очередной открытки. Номера в множествах записаны в порядке приоритетов Александра. Каждый i-й из следующих четырех столбцов содержит номера открыток, которые получит i-й друг из соотвествующих множеств. Наша цель - выбрать для каждого друга самую предпочтительную открытку из его столбца. 

Заметим, что чтобы по текущему множеству Александра и номеру друга определять, какая открытка отправится этому другу, не обязательно знать все множество Александра. Достаточно только двух самых приоритетных открыток. Поэтому для каждого момента времени найдем две самых приоритетных открытки среди имеющихся. Используя их, определим, какая из них отправится каждому другу (посчитаем столбцы таблицы). Потом выберем элемент с максимальным приоритетом в каждом столбце. Получаем решение за O(n2).

Решение 1. Предположим, что ответ на задачу k. Если среди заданных чисел более k одинаковых, то ясно, что мы не сможем их все использовать (потому что мы не можем использовать в одном снеговике одинаковые комы), поэтому оставим из таких комов k, остальные отбросим. Далее отсортируем радиусы в порядке невозрастания. После этого любые два кома с номерами i и k + i различны. Составим снеговиков из комов с номерами (1, k + 1, 2k + 1), (2, k + 2, 2k + 2), (3, k + 3, 2k + 3) и т.д. Если общее количество оставшихся комов не меньше 3k, то у нас всегда получится сделать k снеговиков. Теперь, когда мы умеем отвечать для фиксированного k на вопрос, можно ли составить k снеговиков, можно подбирать k бинарным поиском.

Решение 2. Посчитаем количества комов каждого размера и будем жадно выбирать три наибольшие кучки, брать из них по одному кому и отбрасывать их, и так до тех пор, пока возможно. Почему это правильно? Пусть ответ на задачу k. Если в каких-то кучках больше k комов - будем считать, что их там k, потому что остальные комы мы все равно не используем. Правильность алгоритма докажем через 
Утверждение: если в каждой кучке  ≤ k комов, при этом суммарное количество комов  ≥ 3k, то можно сделать ход по алгоритму. 

Утверждение верно, потому что по принципу Дирихле найдутся хотя бы три непустые кучки. Если есть хотя бы 3 кучки размера k - можно беспрепятственно сделать k шагов алгоритма. Если таких кучек одна или две - первым ходом мы обязательно уменьшим их и перейдем к ситуации для k - 1. Если кучек размера k вообще нет, мы тоже после первого шага получим кучки размером  ≤ k - 1 и суммой  ≥ 3(k - 1). Таким образом, мы всегда сможем сделать k шагов и получить ответ k.  

С точки зрения реализации второго решения удобно посчитать количества кучек с каждым размером комов (при помощи сортировки и "сжатия координат") и использовать set для работы с этими количествами. Время работы обоих решений - .

Решение 1 (жадность). Оптимальный порядок решения задач - в порядке возрастания (неубывания) сложности. При этом задачи, решенные до Нового года, нужно отправлять в 0:00, решенные после Нового года - сразу после их решения.

Почему такой порядок оптимальный, докажем методом спуска. Общая схема рассуждений такова: предположим, что имеется оптимальный ответ, в котором задачи решаются не в порядке возрастания сложности. Покажем, что от него можно перейти ("спуститься") к другому варианту, который будет не менее оптимальным. В итоге такими шагами придем к отсортированному варианту.

Итак, предположим, что в оптимальном ответе есть пара задач, сложности которых идут в порядке убывания. Тогда есть две задачи, решаемые подряд и обладающие этим свойством. Предположим, они обе решаются до Нового года. Тогда от смены их порядка суммарное штрафное время не изменится (а значит, не ухудшится). Если обе задачи решаются после Нового года, то их вклад в общее штрафное время (T + ai) + (T + ai + aj), где T - время начала решения первой из них (с номером i), ai - время решения первой задачи, aj < ai - время решения второй задачи. При перестановке этих двух задач получаем штрафное время (T + aj) + (T + aj + ai), что меньше чем (T + ai) + (T + ai + aj). Осталось рассмотреть случаи, когда одна из соседних задач, стоящих в "неправильном" порядке, "пересекает Новый год". Эти случаи рассматриваются аналогично.

В случае если Геннадий не успевает решить все задачи за отведенное время, следует выбирать наибольшее возможное количество самых простых задач. Действительно, не имеет смысла решать более сложную задачу и не решать более простую: замена большего ai на меньшее не ухудшит ответ. Строгие рассуждения можно провести тем же методом спуска.

Решение 2 (динамика). Сначала, как и в предыдущем решении, выберем наибольшее количество самых простых задач, которые Геннадий успеет решать за отведенное время. Остальные задачи отбросим. Переберем задачу, которая будет решать непосредственно в Новый год (0:00). Остальные задачи, кроме нее, нужно разбить на два множества, одно из которых решается до Нового года, другое - после. Задачи во втором множестве нужно решать в порядке возрастания сложности (известный факт для тех, кто участвует в соревнованиях по правилам ACM). В первом множестве порядок решения неважен. Отсортируем заданные числа по возрастанию и посчитаем динамику d[i][j][k] - наименьшее пенальти, которое можно получить, решив первые i задач, из них j - после Нового года, причем последняя задача после Нового года решена в момент k. Заметим, что по (i, j, k) однозначно определяется количество задач, решенных до Нового года, и суммарное время на их решение. После подсчета динамики вспомним про задачу, которая решалась непосредственно в 0:00 (и которая не участвовала при подсчете динамики). Переберем момент времени до Нового года, когда началось ее решение, и учтем остальные задачи при помощи посчитанной динамики.

Сначала научимся решать подзадачу для одного яруса: составить гирлянду длины s из лампочек ровно k цветов, так чтобы никакие две лампочки одного цвета не шли подряд. При этом варианты, отличающиеся порядком цветов, пока считаем одинаковыми (при необходимости мы всегда успеем домножить на k!). Решение подзадачи нам нужно лишь для k ≤ s ≤ 5000, поэтому считаем динамику за O(s2):
a[s][k] = a[s-1][k-1] + a[s-1][k] * (k -1).
Это были бы числа Стирлинга второго рода, если бы не условие, что одинаковые лампочки не могут идти подряд.  

Далее, посчитаем динамику d[i][j] - количество способов сделать гирлянду для первых i ярусов (с учетом правил), чтобы на i-м ярусе было ровно j различных цветов. Состояний будет порядка L (общей длины гирлянды), потому что на каждом ярусе различных цветов не больше, чем длина яруса: j ≤ li (!). Переходы тоже можно делать за O(L), если учесть тот факт, что множества цветов различной мощности различны (!!). Действительно, положим d[i][j] = Amj * a[l[i]][j] * (сумму всех d[i-1][k]), а потом вычтем варианты, при которых множества на i-м и (i-1)-м ярусах получаются одинаковыми. Количества размещений Amj = m(m - 1)... (m - j + 1) можно предпосчитать, так они нужны только для j до 5000. 

Таким образом, авторское решение работает за O(L + s2) (L ≤ 107, s ≤ 5000), причем не использует деления (только операции умножения и сложения по заданному модулю).

Начнем с того, как выполнить проверку кандидата на центр симметрии (xc, yc). Рассмотрим все точки, симметричные относительно него для (xi, yi). Они имеют вид (2xc - xi, 2yc - yi). Необходимо выяснить, правда ли, что все они, кроме не более k точек, содержатся в множестве {(xi, yi)}. Это можно сделать за бинарным поиском (предварительно отсортировав заданное множество). Однако существует более быстрый способ проверки за O(n). Заметим, что если изначально точки (xi, yi) были упорядочены, скажем, по возрастанию x, а при равенстве x - по возрастанию y, то точки вида (2xc -  xi, 2yc - yi) получатся в порядке, обратном порядку сортировки. Причем вне зависимости от центра (xc, yc). Поэтому если проверять точки (2xc -  xi, 2yc - yi) по порядку, можно просто двигать указатель с конца в отсортированном массиве (xi, yi).

Из предыдущих рассуждений следует, что если множество имеет центр симметрии, то для первой точки (в порядке сортировки) парная n-я, для второй - (n-1)-я, и т.д. Учитывая, что k точек могут не иметь парных, переберем первые (k+1) точку с начала массива и (k+1) с конца. Для каждый пары таких точек найдем середину соединяющего их отрезка и выполним ее проверку за O(n). Асимптотика решения - O(nk2). 
В заключение пару слов о порядке сложности задач. Сложность задачи - величина субъективная. Особенно когда приходится сравнивать идейную задачу с простой реализацией и реализационную задачу почти без идеи. В результате у разных участников получились разные списки предпочтений. Не могу не признать, что порядок, выбранный при подготовке контеста, оказался не совсем адекватен по отношению, например, к количеству решивших задачи, а тем более мог не понравиться кому-то лично. Тем не менее скажу пару слов в его поддержку. А именно, каким принципами мы руководствовались, когда его выбирали.

Количество баллов за задачу - это в первую очередь ее "цена". Умение решать идейные задачи, ИМХО, должно цениться выше, чем умение решать реализационные. Потому что реализацию на уровне задачи B может научиться писать каждый. А вот идея с сортировкой по задаче D на моих глазах не пришла нескольким сильным и опытным участникам. Что касается порядка задач - никто не заставляет вас решать задачи строго по порядку. Ничего плохого нет, если вам быстро приходит идея по задачам C-D, и вы решаете их раньше B и получаете много баллов. Многие так и поступили. Тем более есть текущее положение участников, которым можно руководствоваться при выборе задач.

Полный текст и комментарии »

Разбор задач Codeforces Round 100
  • Проголосовать: нравится
  • +110
  • Проголосовать: не нравится

Codeforces Round #100
Автор natalia, 13 лет назад, По-русски

Всем привет!

Надеюсь, вы уже закончили отмечать Новый год или готовы сделать небольшой перерыв, чтобы принять участие в юбилейном Codeforces Round #100. Раунд состоится 4-го января в 19:00 (Московское время). Это будет общее соревнование для участников обоих дивизионов на одном и том же комплекте из 6 задач. Первые 100 участников по результатам соревнования получат призовые футболки. 

Разбалловка: 500-1000-1500-2000-2500-3000

Как вы уже догадались, в качестве автора задач выступаю я. Неоценимую помощь в подготовке (и даже немного в придумывании) задач оказал Артем Рахов (RAD) и в переводе условий на английский язык - Мария Белова (Delinur).

Под воздействием праздничного настроения условия задач получились про то, как различные персонажи встречали Новый год. Все персонажи и события вымышленные, любые совпадения имен прошу считать случайными :)

Соревнование завершено. От лица команды Codeforces и от себя лично хочу поблагодарить всех, кто принял участие в крупнейшем раунде в истории Codeforces!  К нашему удивлению, 100-е место поделили два участника: pooya_ и Timur_Sitdikov. Конечно же, призовые футболки получат они оба, а также все те, кто оказался выше. Призерам будут разосланы специальные письма по email.

Поздравляем победителей:

1. Egor
4. Petr
6. e-maxx
9. Coder

Полный текст и комментарии »

  • Проголосовать: нравится
  • +314
  • Проголосовать: не нравится

Manthan - заслуженное вознаграждение
Автор natalia, 14 лет назад, По-русски

Manthan прошел на Codeforces где-то в середине марта, побив очередной рекорд по количеству регистраций. Мне по счастливой случайности удалось занять на этом контесте 15-е (последнее призовое) место. Только о моем подарке стоимостью 1000 рупий (по словам Димы Матова, это 600 рублей, не проверяла) ничего не было слышно. Я уже была готова обидеться на организаторов и почти забыла про это соревнование, как вдруг мне приходит письмо. Цитирую только самое интересное.


Congratulations for securing 15th rank in manthan of CodeFest 2011 and winning Gift Vouchers worth INR 1000 from our gifts partner, Naaptol. Please find the details of the GVs as below (along with the terms and conditions):

Дальше приводятся номера ваучеров и прочая секретная информация. Далее:

Conditions: These are very important T&C.
  1. The Gift Voucher (GV) can be redeemed on orders placed at website www.naaptol.com/hot 
  2. Only one order per GV No. (As printed overleaf) can be placed. No two GVs can be clubbed together for an order
  3. This GV is valid till 31st May 2011
  4.  GV is not redeemable/ refundable for CASH and cannot be returned for a cash refund under any circumstances
  5.  If this GV No. is non functional on account of any technical reason, your sole remedy and the sole liability of Naaptol shall be reissue/ replacement of the particular GV NO
  6.  Naaptol is not responsible for the lost or stolen GV and no representation in this regard will be accepted in any form or nature
  7.  This Voucher can be redeemed only by online payment mode. (No cash on Delivery orders will be accepted)
  8. Customer Care - 9223516148
 Вообще использовать подарочные карты в качестве призов - неплохая идея. Только вот приведенный сайт ничего конкретного не сообщает мне о доставке товара, а при выборе конкретного товара предлагает мне указать адрес в Индии :) Еще даже чуть-чуть обидно, что ваучеров два по 500 и их нельзя объединять :(

Извините, что так многословно, просто подобные призы создают определенное настроение :) Интересно,
1. может быть, я чего-то не понимаю и у меня все-таки есть возможность использовать эти деньги в России?
2. на codechef награждать таким образом - обычная практика?
3. что вы думаете по поводу адекватности таких призов на международном соревновании?

В любом случае я благодарна организаторам Manthan, что не забыли :)

Полный текст и комментарии »

  • Проголосовать: нравится
  • +21
  • Проголосовать: не нравится

Предложения по формату соревнований: претесты, сложность задач
Автор natalia, 14 лет назад, По-русски
Три последних "общих" контеста: Codeforces Beta Round #58, Codeforces Beta Round #60 и Manthan 2011, выявили ряд моментов в правилах Codeforces-раундов и вообще принципах их подготовки, которые вызвали разгоряченные споры и недовольство некоторых участников. Самый наболевший вопрос - взломы и их оценивание, я затрагивать не буду. Он обсуждается, например, здесь. 

Хочу выдвинуть такие предложения.

1. После того, как решение участника прошло претесты, нужно открывать их для этого участника.

Какую роль вообще играют претесты? Согласно правилам, "тот факт, что решение прошло претесты говорит только о том, что оно вполне разумно". "Вполне разумно" - понятие расплывчатое, поэтому подбор претестов очень субъективен. Обобщая опыт участия в контестах, могу сказать только то, что в претестах обычно нет максимальных тестов. А вот крайние случаи могут быть представлены в большей или меньшей степени. Цель претестов - с одной стороны, не пустить взламывать тех, кто не может написать хоть какого-то разумного решения по задаче, с другой стороны, оставить некоторый простор для взломов.

Я считаю, что претесты все-таки должны охватывать значительную часть случаев и не пропускать совсем "паленые" решения, как вышло в этом случае. Но они все равно будут пропускать решения с серьезными багами. Даже если автор не хочет этого намеренно, он может не учесть в претестах какого-то распространенного заблуждения участников. Когда я собиралась готовить свой контест, я спросила у Артема Рахова, сколько всего претестов по задаче. Когда я узнала, что их 5-7 (включая примеры из условия!), это сильно изменило мою тактику на контестах: я стала более тщательно тестировать свои решения. Когда нужно гарантированно сдать задачу с первой попытки (например, на школьных олимпиадах), нужно тестировать хотя бы на 10-15 тестах. Причем скорее на 15, если задача сложнее a+b.

Вот и встает вопрос: если решение прошло претесты, нуждается ли оно в дополнительном тестировании? На какие случаи? Открытие претестов даст участнику возможность решить для себя этот вопрос сразу же по ходу соревнования и не обижаться ни на кого потом за слабые претесты. 

2. Выставлять баллы по задачам не обязательно 500-1000-1500-2000-2500, а в соответствии с их реальной сложностью.

Потому что бывает, что задачи A и B, или D и E примерно одинаковые по сложности. Тогда имеет смысл дать за них 750-750 или 2250-2250. Правда, эта идея немного близка к Топкодеру :)

3. При определении сложности задачи учитывать не только сложность алгоритма, но и количество частных случаев в ней.

Эту проблему особенно ярко показал последний контест (Manthan). Задачи D и E (особенно D) опирались на более или менее стандартные алгоритмы и их решение вызвало у многих участников меньше проблем, чем B и C. Тем более, когда идет активный "взломный" процесс, для "взламываемых" и исправляющих свои решения задача все дешевеет и дешевеет. В итоге задачу сдает маленькое количество людей и те, кто сдает, получают совсем небольшие баллы, хотя им пришлось преодолеть значительные трудности. За такие задачи, на мой взгляд, надо давать побольше баллов. Что касается порядка, то ничего страшного, если эти задачи будут A или B - это будет говорить о том, что они не требуют знания чего-то совсем сложного и доступны для начинающих участников. А большая стоимость задачи будет говорить о том, что задача, возможно, содержит подводные камни.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +54
  • Проголосовать: не нравится

Codeforces Beta Round #60: разбор задач
Автор natalia, 14 лет назад, По-русски
Задача A

Рассмотрим сначала случай, когда все числа отличны от нуля. Тогда можно взять a*c*e граммов песка, получить из них b*c*e граммов свинца, из них - b*d*e граммов золота, из них - b*d*f граммов песка. Если b*d*f > a*c*e, то можно неограниченно увеличивать количество песка, а, соответственно, и золота. В противном случае, когда b*d*f <= a*c*e, сколь угодно большое количество золота получить невозможно. То же самое верно, если у дроби (a*c*e)/(b*d*f) только числитель или только знаменатель равен нулю. В противном случае возникает неопределенность 0/0 и нужно делать отдельную проверку случаев.

Поясню, почему я сделала эту задачу именно задачей A. 

1. Для решения задачи требуются совсем незначительные знания по программированию (только if), поэтому она была доступна всем участникам.
2. Хитрые случаи действительно были, но я понадеялась, что "сильные участники ... помогут новичкам отловить все баги своими взломами". Так оно и вышло.

Хотя, возможно, я была не права: эта задача слишком сложная для А. 

Большое количество взломов по этой задаче - вполне предвиденное обстоятельство. Специально оставила большой класс тестов, не вошедший в претесты, чтобы было интереснее ломать. Ради справедливости стоит отметить, что Артем Рахов был против этого. В связи с этой задачей остро всплыла проблема, о которой написал Gassa: претесты отражают весьма неполный набор случаев и заранее непонятно, какой это набор и как интерпретировать событие "решение прошло претесты". Мне кажется, стоит обсудить этот вопрос и четко определить принципы разработки претестов.

Задача B

Полный текст и комментарии »

Разбор задач Codeforces Beta Round 60
  • Проголосовать: нравится
  • +33
  • Проголосовать: не нравится

Codeforces Beta Round #60
Автор natalia, 14 лет назад, По-русски
Рада пригласить всех принять участие в очередном раунде. 

Автором задач сегодня являюсь я. Мы с Артемом Раховым, Марией Беловой и Дмитрием Матовым постарались приложить все усилия, чтобы сделать задачи как можно более надежно.

Надеюсь, задачи окажутся для вас интересными, соревнование динамичным, а сильные участники быстро справятся с задачами и помогут новичкам отловить все баги своими взломами :) 

Удачи!

P.S. Фраза "сильные участники быстро справятся с задачами" ни в коем случае не означает, что все задачи будут простыми. Не забывайте читать условия и тестировать свои решения!

UPD. Соревнование завершено. Поздравляю Kenny_HORROR с победой! 

UPD2. Добавлен разбор задач. Несмотря на рекордное число участников, система во время раунда работала без сбоев. Спасибо команде Codeforces! Всем, кто принял участие в раунде, тоже спасибо.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +134
  • Проголосовать: не нравится

Школьная индивидуальная олимпиада #3 (ЗКШ 2010/11) - Codeforces Beta Round #45 (ACM-ICPC Rules): разбор задач
Автор natalia, 14 лет назад, По-русски
Задачи A и B не представляли идейной сложности, поэтому начнем сразу с C.

Задача C

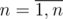Положим β = α / 10. Тогда заданные числа - это a1 = [β], a2 = [2β], a3 = [3β], ... an = [nβ] и нужно определить [(n + 1)β] ([x] - целая часть числа). Данные равенства эквивалентны системе неравеств: an ≤ nβ < an + 1, . Выбирая максимум по левым частям и минимум по правым, получим неравество вида A ≤ n < B. Теперь осталось сравнить целую часть числа A / (n + 1) и B / (n + 1). В случае если B поделилось нацело, нужно вычесть из правой части единичку, т.к. справа неравенство строгое.

Задача D

Создадим векторы vi, в первый из которых v1 будем складывать позиции единичек, в v2 - двоек, в v3 - троек, и т.д. Их можно заполнить за один проход по данной последовательности. Количество перестановок - это количество единичек, или размер первого вектора. Мысленно определим первую единичку в первую перестановку, вторую - во вторую и т.д. Теперь перейдем к двойкам. Если их больше, чем единичек - решения нет. Иначе определим первую двойку в первую перестановку, вторую - во вторую и т.д. Возможно, несколько последних перестановок останутся без двоек. Дальше рассуждаем также для троек (которых должно быть не меньше, чем двоек) и т.д. Получаем решение за O(n). 
 
Задача E

Расскажу два решения. Первое решение разбирает отдельно три возможных случая. Построим граф, вершинами которого являются пары (h, t) - текущие количества голов и хвостов у Змея Горыныча. Ребра определяются возможными ударами Иванушки. Сначала при помощи обхода в ширину определим, можно ли из стартового состояния добраться до (0, 0) и за сколько шагов. Затем проверим, возможна ли ничья. Она возможна, если в графе есть циклы. Иначе граф ациклический и при помощи динамики на ациклическом графе можно определить самый длинный путь до состояния победы Змея.

Второе решение - реализовать алгоритм, который часто пишут для игр на циклических графах. По сути описанный процесс и является игрой на циклическом графе, только ходы Горыныча детерминированы. Начнем с тех состояний, для которых мы знаем ответ, т.е. (0, 0) и h + t >= R, и будем двигаться от них в обратном направлении по ребрам, помечая остальные состояния выигрышнsми или проигрышными. Непомеченные состояния останутся ничейными.

Задача F

Для каждого из n дней необходимо решать так называемую "непрерывную задачу о рюкзаке". Она решается жадно: отсортируем фирмы по цене производимого ими снега и будем брать снег с минимальной цене, пока не наберем нужный объем. Решение с сортировкой при каждом n не проходило по времени. Авторское решение работает за O(nm) и основано на идеях быстрой сортировки (QuickSort). Выберем случайный элемент r на имеющемся отрезке. Как в QuickSort,   переупорядочим остальные элементы, чтобы элементы, меньшие r, шли раньше него, и элементы, большие r - позже. Посчитаем суммарный объем снега с ценами, меньшими r. Если его достаточно - решаем задачу на левом подотрезке. Если нет - покупаем весь левый подотрезок и рекурсивно переходим к правому.

Отмечу еще одну неприятную особенность этой задачи. С одной стороны, ответ может быть достаточно большим. С другой стороны, требуется большая точность. Поэтому нужно вычислять целую и дробную части ответа отдельно.

Задача G

Заданный граф представляет собой связный граф с одним циклом. Сначала научимся решать задачу для дерева. Подвесим дерево за произвольную вершину и стандартной динамикой вычислим для каждого поддерева
1) количество вершин в нем;
2) сумму расстояний от корня до всех вершин поддерева.
После этого мы получим ответ на задачу для корня. Чтобы определить ответ для остальных вершин, совершим еще один обход по дереву. Рассмотрим переход от вершины u к ее потомку v. Чтобы добраться до v из вершни ее поддерева, нужно будет проделать тот же путь, что и до u, только не проходя последнее ребро. Наоборот, для всех остальных вершин путь увеличится на длину этого ребра. Таким образом,  d[v] = d[u] - L(u, v) * c[v] + L(u, v) * (n - c[v]), где c[v] - количество вершин в поддереве с вершиной v.

Теперь перейдем к графу с одним циклом, к которому возможно крепятся деревья. Корнями деревьев будем считать вершины цикла. Посчитаем ответ внутри каждого дерева. Общий же ответ складывается для каждой вершины из:
1) суммы длин путей внутри ее дерева;
2) суммы для всех остальных деревьев путей от их корней до всех вершин в дереве (потому что чтобы добраться до некоторой вершины из другого дерева, нужно пройти через его корень);
3) длины пути от вершины до корня ее дерева, умноженной на общее количество вершин в других поддеревьях;
4) сумма вида <длина кратчайшего пути по циклу от корня до дерева t> * <количество вершин в дереве t>.

Наиболее трудным является вычисление слагаемого 4. Для его подсчета нужно пройти по циклу двумя указателями: на текущую вершину и на вершину в цикле, которая разделяет вершины, от которых надо идти вправо и от которых надо идти влево до текущей вершины. Двигая указатели, можно за суммарное линейное время пересчитывать частичные суммы, необходимые для получения слагаемого 4.

Задача H

Представим сначала, что у нас ровно m черно-белых плиток. Тогда можно поступить следующим образом. Будем перебирать клетки по порядку сверху-вниз слева-направо. Сначала положим a черны плиток, потом - c = m черно-белых, затем - b белых. В итоге образуется граница из черно-белых плиток, разделяющая черные и белые. Эти плитки можно повернуть так, чтобы замощение стало корректным. Например: n = m = 4,
a = b = 6, c = 4.

########
########
#####/\#
####/..\
\##/....
.\/.....
........
........

В общей ситуации заменим c - m черно-белых плиток, например, на белые и построим замощение. Затем заменим белые плитки обратно на черно-белые, начиная с правого-нижнего угла, например: n = m = 4, a = 6, b = 3, c = 7.

########
########
#####/\#
####/..\
\##/....
.\/.....
.../\../
../##\/#

Решение в задаче всегда существует.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +31
  • Проголосовать: не нравится

Школьная индивидуальная олимпиада #3 (ЗКШ 2010/11) - Codeforces Beta Round #45 (ACM-ICPC Rules)
Автор natalia, 14 лет назад, По-русски

Добрый день!

Приглашаю всех принять участие в соревновании, завершающем серию заочных олимпиад ЗКШ для школьников и одновременно являющемся очередным Codeforces-раундом. Начало соревнования - 12 декабря, в 11:00 по московскому времени. 

Соревнование пройдет по правилам ACM-ICPC, продолжительность контеста - 3 часа.

Как и предыдущие школьные индивидуальные олимпиады, соревнование будет рейтинговым для всех участников (и для школьников, и для остальных). Рейтинг будет вычисляться в соответствии с объединенной таблицей результатов.

В качестве авторов задач снова выступаем я и Дмитрий Матов. Спасибо Геральду Агапову и Артему Рахову за помощь в подготовке задач и Марии Беловой за перевод условий.

Всем удачи!

UPD. Соревнование завершено. Доступны результаты. В школьной индивидуальной олимпиаде победил scottai1, в Codeforces Beta Round - ilyakor. Поздравляем победителей! 

Опубликован авторский разбор задач. Теперь в разбор добавлены также задачи G и H.

Спасибо всем, кто принял участие в серии заочных олимпиад ЗКШ в конкурсе и вне конкурса!



Полный текст и комментарии »

  • Проголосовать: нравится
  • +85
  • Проголосовать: не нравится

Школьная индивидуальная олимпиада #2 (ЗКШ 2010/11) - Codeforces Beta Round #43 (ACM-ICPC Rules): разбор задач A, C, F и G
Автор natalia, 14 лет назад, перевод, По-русски
Задача A

Задача решается простым моделированием описанного процесса. Главное - правильно обработать переход через n. Это можно сделать либо взятием номеров по модулю n (с прибавлением 1), либо вычитать n каждый раз, как текущий номер стал больше n.

Задача C

Сначала посчитаем, сколько в последовательности хомячков.  Пусть их h. Переберем позицию, в которой будет начинаться последовательность хомячков, и для каждой начальной позиции посчитаем, сколько тигров оказалось в отрезке h, начиная с этой позиции.  Этих тигров придется поменять с хомячками за количество обменов, равное количеству тигров, стоящих не на своем месте. Выберем минимум по всем начальным позициям.

Задача F

Во-первых, заметим, что все описанные операции (открытие/закрытие дверей, перемещения из одной комнаты в другую, обмен ключами) обратимы. Поэтому можно применить несколько таких операций из начального расположения и получить некоторое расположение A, и затем получить то же расположение А путем применения подобных операций из конечного расположения, в этом случае ответ будет "YES". Применим следующую стратегию к обоим расположениям: пока существует человек, который может перейти в некоторую комнату и открыть некоторую дверь, выполнять это действие. В результате для каждого из расположений мы получим связные подмножества комнат (будем называть из связными частями дома), соответствующие подмножества людей и ключей в каждой связной части дома. Если результирующие подмножества совпадают для начального и конечного расположения, то ответ на задачу "YES", иначе ответ "NO". Действительно, в случае совпадения можно очевидным образом из начального расположения получить результирующее, а из него - конечное. В противном случае это невозможно сделать, потому что найдутся ключи, которые не могут быть применены к соответствующим дверям, находящимся в другой связной части дома,  или найдутся люди, которые не имеют возможности проникнуть в комнаты, расположенные в другой связной части дома.

Во-вторых, несколько слов о реализации. Один из возможных способов - хранить две булевы матрицы
1) определяющую для каждого человека, может ли он попасть в каждую из комнат, и
2) определяющую то же самое для каждого ключа,
и рекурсивно выполнять операции:
1) если человек может оказаться в комнате, попробовать сделать переходы в соседние комнаты,
2) то же самое для ключей, пытаясь при этом открывать дверь в соседнюю комнату,
3) когда дверь открывается, сделать переход для людей и ключей в смежных комнатах.

Таким образом, мы перебираем каждую пару человек-комната, человек-дверь, дверь-ключ, дверь комната O(1) раз, поэтому общая асимптотика решения O(nk + km + m2 + nm).    

Задача G

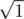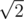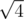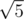Заметим, что длинами сторон могут быть числа , , , и т.д., т.е. корни целых чисел, представимых в виде 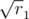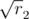a2 + b2. Сгенерируем достаточное количество таких чисел. Обозначим их , , ... В некоторых случаях можно взять в качестве длин сторон первые n чисел, но в некоторых случаях этого сделать точно нельзя. Все зависит от четности. Если сумма r1 + r2 + ... + rn нечетна, это невозможно сделать. В самом деле, каждую сторону можно представить вектором  (xi, yi), xi2 + yi2 = ri (xi и yi могут быть отрицательными).  Если число ri четно, сумма xi + yi также четна. Если ri нечетно, то и xi + yi нечетно. Если можно построить многоугольник с векторами сторон (xi, yi), то x1 + x2 + ... + xn = 0 и y1 + y2 + ... + yn = 0, поэтому общая сумма x1 + ... + xn + y1 + ... + yn должна быть четной! Но если сумма r1 + ... + rn нечетна, она также нечетна, и построить многоугольник невозможно.

Возьмем числа r1, ..., rn, если их сумма четна, иначе возьмем r1, ..., rn + 1 и выбросим одно из них, чтобы сделать сумму четной (в своем решении я выбрасываю наибольшее из таких чисел). Для каждого ri выберем неотрицательные xi и yi, xi2 + yi2 = ri. В общем случае существует 8 возможных ориентаций вектора (xi, yi), ( - xi, yi), (xi,  - yi), ( - xi,  - yi), (yi, xi), ( - yi, xi), (yi,  - xi), ( - yi,  - xi). Решим следующую подзадачу - заориентировать векторы таким образом, чтобы их сумма равнялась нулю. Это можно сделать при помощи следующего жадного алгоритма. Будем перебирать векторы, начиная с наибольших по длине. Будем вычислять текущую векторную сумму, которая изначально равна (0, 0) и будет пересчитываться при каждом добавлении вектора. На каждом шаге будем выбирать ориентацию, минимизирующую текущую сумму (по длине) при добавлении к ней. Затем, когда векторы заориентированы, отсортируем их по полярному углу и, прибавляя их последовательно, получим выпуклый многоугольник. Описанный алгоритм находит требуемый многоугольник на всех возможных тестах.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +28
  • Проголосовать: не нравится

Школьная командная олимпиада #2 (ЗКШ 2010/11): разбор задач A-E, H, J
Автор natalia, 14 лет назад, По-русски
Задача A

Один из возможных путей решения задачи - сравнивать каждый листик с уже взятыми. Если он совпал с одним из них, тогда его не нужно брать. Поскольку порядок листьев неважен, можно просто отсортировать их (например, как пары строк) и удалить одинаковые листья.

Задача B

Задача заключается в нахождении количества троек (x, y, z), таких что 0 <= x <= a, 0 <= y <= b, 0 <= z <= c и 0.5 * x + y + 2 * z = n. Перебор всех троек работает долго, однако все возможные значения x и y, удовлетворяющие неравенствам 0 <= x <= a, 0 <= y <= b перебрать можно. Когда x и y фиксированы, значение z определяется однозначно. Получаем решение за O(a*b).

Задача C

Самое простое решение - перебрать все дни с 1 до n и для каждого дня проверить, что он покрывается ровно одним отрезком [ai, bi]. Если обнаружен день, который покрывается  меньшим или большим количеством отрезков, выведите этот день.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +5
  • Проголосовать: не нравится

Школьная командная олимпиада #2 (ЗКШ 2010/11)
Автор natalia, 14 лет назад, перевод, По-русски
Всем добрый день!

Я рада пригласить вас принять участие в следующем раунде серии зимних школьных олимпиад по информатике, который состоится 6 ноября в 14:00 MSK. 

Соревнование будет официальным для команд школьников и неофициальным и нерейтинговым для всех остальных. Напоминаю, что если у вас школьная команда, то вы должны зарегистрировать всех участников для участия в серии, если вы еще этого не сделали.

Продолжительность соревнования 5 часов, правила - стандартные для ACM ICPC. 

В подготовке задач участвовали я, Дмитрий Матов, Полина Бондаренко, Михаил Мирзаянов, а также Мария Белова, которая перевела их на английский. Мы все надеемся, что вам будет интересно поучаствовать в соревновании.

Удачи!  

UPD. Условия в PDF: русская версия и английская версия. Условия будут доступны, как только начнется соревнование.

Соревнование завершено. Победил Геннадий Короткевич, решивший 9 задач менее чем за 3 часа. Доступны результаты. 

Разбор задач:

Полный текст и комментарии »

  • Проголосовать: нравится
  • +23
  • Проголосовать: не нравится

Школьная командная олимпиада #1 (ЗКШ 2010/11): разбор задач
Автор natalia, 14 лет назад, По-русски
Задача А

Для получения максимального возможного результата нужно просто отсортировать слагаемые в порядке неубывания коэффициентов (коэффициенты учитываются со стоящими перед ними знаками + и -). Не нужно обращать внимание на a++ или ++a! Вопрос заключается в том, почему это правильно.

Во-первых, рассмотрим выражение, содержащее только a++. Тогда наше утверждение очевидно: выгодно умножать 'a' на маленькие коэффициенты, пока значение 'a' маленькое, и на большие коэффициенты, когда оно становится больше. То же самое происходит в случае трицательных значений коэффициентов или 'a'. Конечно, это не строгое доказательство. Я надеюсь, что вы еще подумаете над ним, если пока не поняли.

Во-вторых, рассмотрим выражение k*a+++k*++a, где k - некотрый коэффициент, одинаковый для обоих слагаемых. Пусть начальное значение 'a' равно a0. Вычисляя значение выражения обоими способами, получаем: k * a0 + k * (a0 + 2) =  k * (a0 + 1) + k * (a0 + 1). Поэтому в данном случае порядок неважен.

В-третьих, пусть наше выражение k*a+++l*++a, где k и l - различные коэффициенты. Это выражение может принимать два разных значения k * a0 + l * (a0 + 2) и k * (a0 + 1) + l * (a0 + 1). Первое значение больше второго тогда и только тогда, когда k < l. Аналогично можно рассмотреть выражение k*a+++l*++a.

Таким образом, если имеются два последовательных слагаемых с одним и тем же коэффициентом, мы можем переставлять или не переставлять их. Если имеются два последовательных слагаемых с различными коэффициентами, мы должны поставить раньше то слагаемое, у которого коэффициент меньше. Применяя эти рассуждения, пока необходимо, получаем последовательность слагаемых отсортированных по коэффициентам.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +9
  • Проголосовать: не нравится

Школьная командная олимпиада #1 (ЗКШ 2010/11)
Автор natalia, 14 лет назад, перевод, По-русски
Добрый день всем!

Приглашаем всех на Школьную командную олимпиаду #1, которая состоится 24 октября в 11:00 MSK. Соревнование будет официальным для команд школьников, как часть серии школьных заочных олимпиад ЗКШ (http://codeforces.net/blog/entry/753), и неофициальным (и не рейтинговым!) для всех остальных.

Чтобы принять участие официально, каждый участник школьной команды должен сначала зарегистрироваться лично, затем из зарегистрированных участников нужно создать команду и, когда будет открыта регистрация на соревнование, зарегистрировать команду еще и там.

Надеюсь, что задачи окажутся интересными для школьников с разным уровнем подготовки в программировании, и не только для школьников! Обратите внимание на некоторые отличия от обычных соревнований на Codeforces. Во-первых, продолжительность соревнования 5 часов, и будут стандартные правила ACM ICPC. Во-вторых, задачи не будут идти в порядке возрастания сложности, они будут перемешаны. Поэтому ваша первая задача - найти простую задачу :)

Авторы задач - Михаил Мирзаянов и я. Спасибо Геральду Агапову, Полине Бондаренко  и Артему Рахову, которые помогали мне готовить раунд. Также спасибо Марии Беловой за перевод условий задач на английский язык. Мы все - сотрудники и студенты Саратовского Государственного Университета.

Удачи!

P.S. Будьте внимательны при регистрации на соревнование. Аккуратно читайте все всплывающие сообщения. Для участия в конкурсе должна быть зарегистрирована команда, все члены которой зарегистрировались для участия в серии. В команду должны быть приглашены (и подтвердить свое участие) все те, кто собирается писать соревнование.

UPD: Как только начнется соревнование, то будут доступны задачи в PDF (для печати):
UPD: Соревнование завешено. Доступны результаты.Победителем и в официальном, и в общем зачете стал Gennady Korotkevich, решивший все задачи. Поздравляем победителя! Доступен разбор задач.

Полный текст и комментарии »

  • Проголосовать: нравится
  • +29
  • Проголосовать: не нравится

Codeforces Beta Round #36 (Разбор задачи E)
Автор natalia, 14 лет назад, перевод, По-русски
В задаче требуется разбить ребра графа на две группы, каждая из которых образует путь в графе. Ясно, что каждый путь содержится в одной компоненте связности. Поэтому если в данном графе больше двух компонент связности, то задача не имеет решения. То же самое можно сказать про граф, в котором более четырех вершин нечетной степени. Действительно, каждая вершина в пути имеет четную степень, за исключением первой и последней вершины. Поэтому объединение двух путей не может содержать больше четырех нечетных вершин.

Теперь рассмотрим случаи:

1. Одна компонента связности, нет вершин нечетной степени. Тогда имеем эйлеров цикл, который можно разбить на два пути.

2. Одна компонента связности, две нечетные вершины. То же самое, только с эйлеровым путем вместо эйлерова цикла. Есть один хитрый случай: граф с одним ребром, который не может быть разбит на два непустых пути.

3. Одна компонента связности, четыре нечетные вершины. Самый интересный случай. Соединим две вершины нечетной степени фиктивным ребром. Получим граф, содержащий эйлеров путь. Найдем эйлеров путь и удалим фиктивное ребро - получим два пути.

4. Две компоненты связности, каждая имеет ноль или две нечетные вершины. Два эйлеровых пути/цикла.

5. Две компоненты связности, четыре нечетные вершины в одной и ни одной нечетной вершины в другой. Нет решения.

Полный текст и комментарии »

Разбор задач Codeforces Beta Round 36
  • Проголосовать: нравится
  • 0
  • Проголосовать: не нравится

Codeforces Beta Round #36 (Разбор задачи D)
Автор natalia, 14 лет назад, По-русски
В задаче описывается игра на ациклическом графе. Состояниями (вершинами графа) являются пары (n, m), где  n и m - расстояния от текущей позиции фигуры до нижнего и правого краев доски соответственно. Из каждого состояния (n, m) существует не более трех переходов: (n - 1, m), (n, m - 1), (n - k, m - k).  Граф ациклический, поскольку при каждом переходе сумма n+m строго уменьшается. 

Если бы n, m и k в задаче были, скажем, до 1000, то задача решалась бы несложной динамикой на ациклическом графе, стандартной для подобных игр. Пусть d(n, m) = 1, если (n, m) - выигрышная позиция, и d(n, m) = 0, если позиция (n, m) - проигрышная. Тогда d(n, m) вычисляется из следующих соображений: если из позиции существует хотя бы один переход в проигрышное состояние, то эта позиция выигрышная, иначе она проигрышная.

Но ограничения в задаче не позволяют решать ее обычной динамикой. Выход из ситуации - посчитать динамику для маленьких значений n и m и заметить закономерность! Например, построим матрицу значений d(n, m) при k = 2:

01010101010101
10101010101010
01111111111111
10110101010101
01101010101010
10110111111111
01101101010101
10110110101010
01101101............

Полный текст и комментарии »

Разбор задач Codeforces Beta Round 36
  • Проголосовать: нравится
  • +12
  • Проголосовать: не нравится

Codeforces Beta Round #36 (Разбор задачи B)
Автор natalia, 14 лет назад, По-русски
Авторское решение задачи строит фрактал при помощи рекурсивной функции. Пусть a - квадратная матрица размера nk × nk для записи результата. Напишем функцию fractal(x, y, k), которая заполняет квадратную часть матрицы с левым верхним углом (x, y) и длиной стороны nk, рисуя в ней фрактал с глубиной k. В случае если k = 0 выводим точку. В противном случае требуется разбить имеющуюся часть матрицы на n2 квадратов размера nk - 1 × nk - 1 и заполнить их в соответствии с шаблоном. Если соответствующий символ в шаблоне ''*'', то нужно весь квадрат заполнить символами ''*'', иначе запустить fractal(x1, y1, k-1), где (x1, y1) - координаты левого верхнего угла нового квадрата.

Более простое в реализации решение предлагает kdalex (http://codeforces.net/blog/entry/764). Переберем все клетки (x, y). Если для какого-то c = nd, 0 ≤ d < k клетка ((x/c)%n, (y/c)%n) шаблона черная, что и (x, y) - черная, иначе (x, y) - белая. Нетрудно видеть, что если при d = k - 1 клетка ((x/c)%n, (y/c)%n) черная, то получается, что наша клетка (x, y) попала в черный квадрат на первом шаге алгоритма. Если ((x/c)%n, (y/c)%n) черная при d = k - 2, то на втором шаге и т.д.

Полный текст и комментарии »

Разбор задач Codeforces Beta Round 36
  • Проголосовать: нравится
  • +2
  • Проголосовать: не нравится