Hello Codeforces people, I have a question about problem 442C - Artem and Array . I looked at the solution in the tutorial, and I have no problem with it. Nevertheless, this is what I was trying before looking at the solution (let v[i], for i = 1, ..., n be the i-th element of the array):

• First, notice that we can choose the first and last element of the array right at the end (they will be our last choices)
• Second, we can choose the k-th element to be our penultimate choice (thus obtaining min(v[1], v[n]) points).

We can then solve the problem using dynamic programming: just let f(a, b) be the maximum number of points Artem gets when he plays with the (sub)array v[a..b].

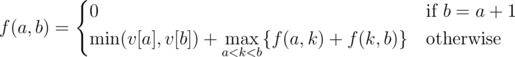
This is a O(n³) solution, the answer to the problem is f(1, n). From here, was there something I could have noticed to get the running time down to O(n²) or ?

The only things I proved are that f(a, b + 1) ≥ f(a, b) and f(a - 1, b) ≥ f(a, b). If I'm not wrong, the official solution implies that the best k for f(a, b) is always the one for which v[k] is maximum.

Hi there, Codeforces community! This question has been bugging me for a while now, so I thought I would share it with you, and see if we can work out the answer together.

The problem is the following: given an array of n integer numbers (positive and negative), find a (contiguous) subarray for which the product is maximum. I would like to find an algorithm with complexity less than O(n²).

For instance, if the array is

then the underlined subarray would be the one we are looking for (its "score" is 7×4 = 28) .

Notice that if we changed "sum" into "min" the problem would be solvable in time. Similarly, if we changed "sum" into "gcd" the problem would still be solvable in time. (I can elaborate if you are interested). The problem is, with other associative operations, such as sum or product, I don't know how to go down from n² to something less.

Any clue?