Hi there, Codeforces community! This question has been bugging me for a while now, so I thought I would share it with you, and see if we can work out the answer together.
The problem is the following: given an array of n integer numbers (positive and negative), find a (contiguous) subarray for which the product 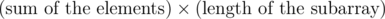 is maximum. I would like to find an algorithm with complexity less than O(n2).
is maximum. I would like to find an algorithm with complexity less than O(n2).
For instance, if the array is
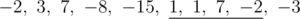
then the underlined subarray would be the one we are looking for (its "score" is 7×4 = 28) .
Notice that if we changed "sum" into "min" the problem would be solvable in  time. Similarly, if we changed "sum" into "gcd" the problem would still be solvable in
time. Similarly, if we changed "sum" into "gcd" the problem would still be solvable in  time. (I can elaborate if you are interested). The problem is, with other associative operations, such as sum or product, I don't know how to go down from n2 to something less.
time. (I can elaborate if you are interested). The problem is, with other associative operations, such as sum or product, I don't know how to go down from n2 to something less.
Any clue?











We'd just need to take either the whole array, or nothing. So, this is O(n).
Ahah, you're right! I meant "min" (I edited the post, thanks)
LOL , it is still solvable in O(n) time.
for every i find nearest integer smaller than i'th integer from left and from rightز
more formally:
let L[i] equal to largest j such that j<i and A[j]<A[i]
and R[i] equal to smallest k such that i<k and A[i]>A[k]
then the answer is max( ( (R[i]-1) — (L[i]+1) + 1) * A[i] ) for all i
finding the values of L and R can be done using stack in O(n)
this is similar problem HISTOGRA
Yes, this was also my solution indeed. Only difference I was computing those L[i] and R[i] values using a binary search for each i.
But then you're right, it is possible to compute L and R inductively in O(n) time.
The point is: can we still solve the problem efficiently if we change that "min" into a "sum"?
Not if negative numbers are allowed.
if there exists atleast one non-negative integer, then choose the entire array as the subarray, and the answer will be maximized.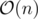 it is!
it is!
if not, then choose the least negative integer (single element) as the subarray, and the magnitude of the answer (which will be negative) will be minimized.
so
Hm not sure what I was thinking :D I guess I was thinking about sums. Of course you're right.
For the example the answer should be 66.
Yes, you're absolutely right. Sorry for that, I fixed the example :)
Hi
Could you please elaborate this?
"Similarly, if we changed "sum" into "gcd" the problem would still be solvable in time. (I can elaborate if you are interested)."
Thanks
There can be only different gcd values among suffixes of an array (due to Euclide's algorithm complexity). So you can add characters one by one keeping all possible gcd's of current array's suffixes.
different gcd values among suffixes of an array (due to Euclide's algorithm complexity). So you can add characters one by one keeping all possible gcd's of current array's suffixes.
By the way, does anyone know solution for the original problem now, 2 years later?
How to implement adding in O(nlogn) ?
For each gcd keep the min and max length of suffixes which has such gcd. After that when you want to add element, for each segment compute gcd with this new element and update the borders. Also you should add one new segment which contains only that element. You should glue segments with same gcd when you do so.
I was thinking to try something like the solution of GSS3 Link to the problem... The idea is to save the answer for a suffix and a prefix subaaray for particular segment and also saving the subarray with maximum( sum* length) for that segemnt. Then keep merging them to get the answer for the whole array. I implemented a solution using segment trees (Link).
You can check on some testcases. I don't know if its completely correct. Just thought to share the idea :P . Maybe it can be implemented without segment trees because we don't need to save the answer for every node.
But what do you store for the prefix and suffix? The entire difficulty in the sum * length problem is that there isn't 1 optimal suffix/prefix.
If the values compared in the merge() function are equal then any of them could produce a larger answer later on while building a tree. I didn't think of it before. It might be the problem in this approach.
But saving the suffix and prefix with maximum sum * length is not necessarily correct.
Consider the case where the left 'subtree' is
-1 -1 -1 -1and the right 'subtree' is100 100 100 100.The suffix of the left subtree with greatest sum * length is the empty suffix with sum * length = 0. But the optimal solution is to take the entire string since the sum in the right subtree outweighs the negative sum in the left subtree. (And you can't fix this by adding it as a special case, the optimal suffix in the left subtree could be any length.)
For array
it produces answer 36, whereas correct answer is 56.
So I think we got the problem here.. thanks gendelpiekel and Shapo for taking the time to read the code. This might be the problem in this approach.
I have a solution to propose but I'm sure I made mistakes everywhere. Probably I even made a mistake immediately and this makes no sense.
Firstly, we can restate the problem. Consider the graph (as in x-axis y-axis graph, not nodes + edges graph) of the cumulative sums. We wish to find the greatest (positive) rectangular area between two points.
Secondly, consider two points which we are considering to use as the 'bottom left' corner of the rectangle, call them P = (x0, y0), Q = (x1, y1). Without loss of generality (wlog) let us say x1 > x0.
Observe firstly that if x1 >= x0 and y1 >= y0, we will always choose P over Q. So we can say y1 < y0. I.e. we only need to consider a set of points that become lower as you move right.
Now, which points T = (x, y) are there such that we wish to choose P over Q? I claim they are the points above the line going through (x0, y1) and (x1, y0). Diagram (we should choose P if T is above the red line, otherwise we should choose Q):
Now things get very hand-wavy and probably wrong or suboptimal.
Let's call the red line the 'optimality line' of P and Q.
Now we wish to solve the problem: given some potential 'bottom-left' points (call them 'candidates'), which is the best to use for some given query points? We can solve the problem for 2 candidates, but how do we solve it for more than 2?
Consider 3 candidates. Call them P, Q, R in order of increasing x (remember that this means they are also in order of decreasing y). The optimality lines between P and Q, P and R and Q and R will all interesect at the same point. Example diagram (P = (0,4), Q = (2,3), R = (4,0):
Purple, green and orange areas are where R, Q and P are optimal respectively.
I believe (*wave hands*) that it should be a similar case for any 3 candidates (*wave hands more*). So for any 3 candidates, we should be able to calculate the x coordinate at which the middle candidate becomes redundant.
So now, we can sweep from left to right to answer queries. As we move, we calculate when each point will become redundant and remove them as necessary. (*wave hands vigorously*)
To answer the queries themselves, we can binary search over the currently valid candidates (in order of the y values where they are optimal).
blah blah something something it seems O(n lg n) maybe. (edit actually maybe n lg^2 n, who knows) (more edit: actually probably still n lg n)
Okay I'm going to sleep now. I missed quite a few details and this is pretty poorly written because I had to change my solution as I realised some parts were wrong. Tomorrow I will probably wake up, read this and realise I'm totally insane >_>
edit: 1) actually maybe you need a set to store candidates since you (might?) have to remove from the middle (?) so it would be O(n lg^2 n), 2) there's lot's of implicit details about keeping the candidates in order of decreasing y value, blah blah details something something
mote edit: actually binary search is separate from set operations so probably still n lg n (okay I'm actually going to sleep now)
you slightly missed areas of optimality: green area will be not in bottom, but in opposite direction
* Assume we have only bottom-left candidates (we can calculate in O(N) using stack).
* Assume that for every 3 consecutive candidates optimality lines aren't parallel (if not, we can completely remove middle candidate, because it won't be optimal anywhere). Then, if we can prove that for every 3 candidates optimality lines intersect in one point (Sympy suspects it is true), we can prove by induction that for every set of candidates their pairwise optimality lines intersect in one point. Therefore, the whole plane divided into sectors, and every sector corresponds to one candidate, which is optimal here.
* Moreover, we can compute this division in O(K), where K — number of candidates, because every sector is defined by two optimality lines between one candidate and its neighbours (for first and last candidate we pick last and first one, respectively).
* After that, each query processed in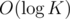 : you just simply find sector containing query poing using binary search.
: you just simply find sector containing query poing using binary search.
So, we have solution in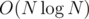 .
.As for other part — nevermind, it's bullshit about induction
Hmm... I'm pretty sure the green area is correct in my diagram. For example consider T = (4, 4), it is clear we should choose Q = (2, 3) as our bottom left point.
But you're right, there are cases where the 'green' area is above instead of below. Specifically: the green area is below when Q is above (the line) PR, the green area is above when Q is below PR. Also, as you pointed out, there are cases where the lines actually don't intersect, which is when Q is on PR.
So in fact there are cases where we should add candidates as we sweep from left to right, not just remove (and cases when we don't add or remove the candidate at all).
Also, I think that we might actually not be able to consider only the two adjacent points when calculating when to add or remove a point. Probably we can't without more observations and maybe not at all.
So actually, perhaps we can't do better than sqrt decomposition and the final solution is quite similar (or perhaps identical) to the half plane solution you described.
Yes, you're absolutely right about green area. I found mistake in my thoughts.
Isn't this idea like convex hull trick in 3D? For each j we want to find i < j maximizing (j - i)(pi - pj) = jpj - ipj - pij + ipi; jpj is constant, so we have a collection of planes z = - ix - piy + ipi and need to find the topmost of them for (x, y) = (j, pj) each time. It looks hard in general case.
Disclaimer: It took slightly complicated :) I don't think it's the best solution ever, moreover I can miss something. So, comments and questions are welcome!
Assume we have array of n integer numbers indexed 1 trough n. Let's denote Ai as i-th number in this array.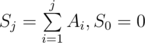 . Now we try to solve the following problem equivalent to the original one:
. Now we try to solve the following problem equivalent to the original one:
First of all, calculate array of prefix sums named S, so that
Now let's make a hypothesis that we have a data structure, which operates on points in 2-dimensional space and allows to:
Given such a data structure, one can use SQRT-decomposition:
In total we have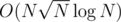 complexity.
complexity.
As for data structure, I'd like only to mention the key ideas:
Okay, I think I have an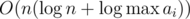 solution.
solution.
Let's make a binary search on the answer. Now we want to know if there are indices L, R so that (aL + 1 + ... + aR)(R - L) ≥ M for fixed M. Set Sk = a1 + ... + ak, then the inequality above becomes (SR - SL)(R - L) ≥ M. Solving for SR, we get:
Let's make a set of functions f1, ..., fn so that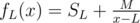 for x > L. Now we want to see if there are any L, R for which fL(R) ≤ SR, that is, when we set f(x) = min fi(x), if there is any R such that f(R) ≤ SR.
for x > L. Now we want to see if there are any L, R for which fL(R) ≤ SR, that is, when we set f(x) = min fi(x), if there is any R such that f(R) ≤ SR.
How to compute f? Notice that each fL is a hyperbola. We can easily see that:
(It is a bit messy, but I gave you an idea). The running time is now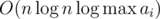 , however we can sort everything only in the beginning of the runtime. This brings down the running time to what I stated.
, however we can sort everything only in the beginning of the runtime. This brings down the running time to what I stated.
nvm
There were some inequalities reversed, it should be okay now.