Sometimes I wonder, what implementation of a segment tree to use. Usually, I handwave that some will suit, and that works in most of the cases.
But today I decided to back up the choice with some data and I ran benchmarks against 4 implementations:
- Simple recursive divide-and-conquer implementation Code
- Optimized recursive divide-and-conquer, which does not descend into apriori useless branches Code
- Non-recursive implementation (credits: https://codeforces.net/blog/entry/18051) Code
- Fenwick Tree Code
All implementations are able to:
-
get(l, r): get sum on a segment (half-interval) $$$[l; r)$$$ -
add(i, x): add $$$x$$$ to the element by index $$$i$$$
Here are the results: 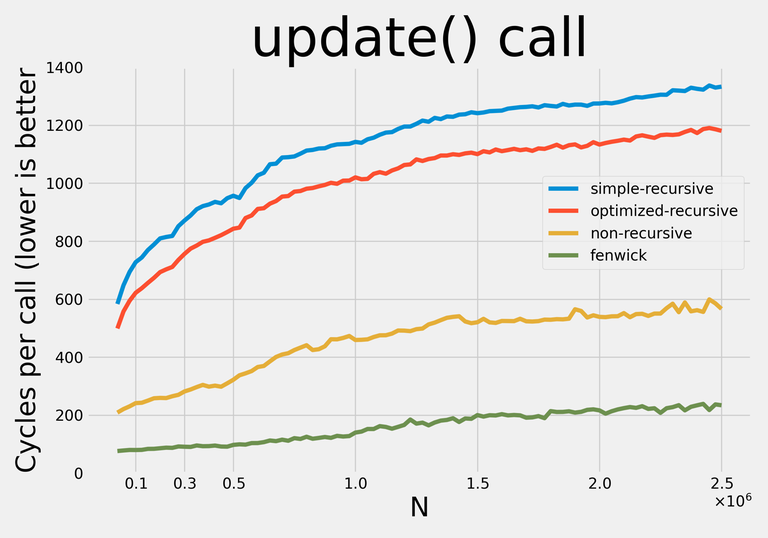
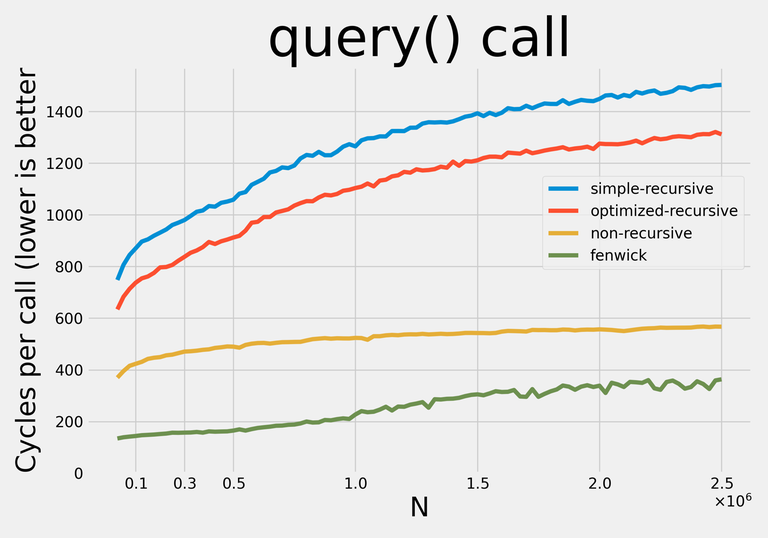
Note: I decided not to apply any addition-specific optimizations so that with minor modifications the data structures could be used for any supported operations.
I generated queries the following way:
- Update: generate random index (
rnd() % size) and number - Query: at first, generate random length (
rnd() % size + 1), then generate a left border for that length
Benchmarking source code. Note that ideally you should disable frequency scaling, close any applications that might disrupt the benchmark (basically, the more you close — the better) and pin the benchmark process to a single CPU (core).
My benchmarking data in case you want to do some more plotting/comparing.
I compiled the benchmark with #pragma GCC optimize("O3") on GNU GCC 11.3.0, and ran it with the CPU fixed on 2.4 GHz, the process pinned on a single CPU core and the desktop environment closed.
This is probably my first useful contribution so any suggestions/improvements are welcome.










