I had nothing to do these eve, so I've collected data via codeforces api from the last three contests where was an enormous number of cheating attempts. With total number of approximately 4000 skipped submissions on problem A in these contests, the distribution of the cheaters that specified their countries is the following: 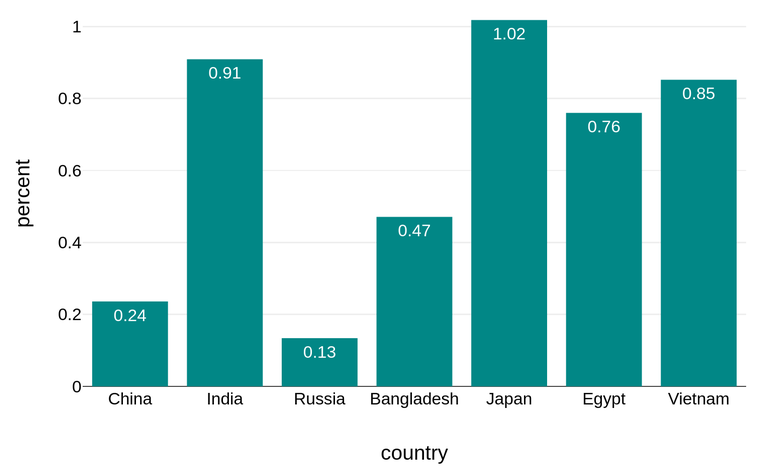
Assuming that those 3000 people that didn't specified their countries are distributed uniformly among the countries, the cheating leader is Japan, not India (though, it is very close to Japan and has the second place). Countries that are not depicted have $$$\le 10$$$ cheaters.
But still I think that most "anonymous" users are from India.









