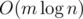Можно найти всю информацию о столкновениях i-той машинки в i-той строке матрицы A. А именно, если в i-той строке есть хотя бы одна из цифр 1 или 3, то i-тая машина не является хорошей (она перевернулась при каком-то столкновении). Иначе, i-тая машина — хорошая. Теперь нам просто нужно проверить это условие для каждой машинки.
Можно заметить, что если si = ti для некоторого i, то значение pi для нас не важно. В самом деле, если pi равно si, то оно также равно и ti. И если pi не равно si, то оно также не равно и ti. Так мы получаем ответ, который одновременно ближе или дальше от обоих строк s и t.
Тогда нам интересны такие позиции i, что si ≠ ti. Если мы положим pi равным si мы увеличим расстояние от p до t. Если мы положим pi равным ti то мы увеличим расстояние от p до s. Это означает, что нам необходимо разделить эти позиции на две равные по количеству группу, чтобы получить равноудалённую строку. Например, мы можем сделать так, чтобы первая из этих позиций была ближе к s, вторая к t и т.д. Если таких позиций чётное количество, то мы получим ответ, если нечётное, то ответа не существует.
Временная сложность — O(n).
Задачу можно решить с помощью динамического программирование или с помощью жадного алгоритма. Начнём с динамики.
Обозначим через stayi, lefti and righti наибольшее количество деревьев, которые дровосеки могут повалить, если существует только деревья с номерами с 1 по i, и i-тое дерево не срублено, i-тое дерево срублен и повалено влево, i-тое дерево срублено и повалено вправо соответственно. Теперь мы можем посчитать эти значения для каждого i от 1 до n за O(n) времени, потому что для вычисления каждой следующей величины нам нужно только две предыдущих. Ответом будет наибольшее из stayn, leftn, rightn.
Также эту задачу можно было решить жадным алгоритмом. Давайте повалим самое левое дерево влево (это никогда не ухудшает ответ). После этого, попробуем повалить следующее дерево. Если мы можем повалить его влево, сделаем это (потому что это также никогда не ухудшает ответ). Если не можем, тогда пробуем повалить вправо. Если это возможно, делаем это. Последний шаг справедлив, потому что сваливание некоторого дерева вправо может помешать только сваливанию следующего дерева. Так что мы можем "обменять" одно дерево на другое, не ухудшив ответа.
Временная сложность — O(n).
Можно решить задачу с помощью жадного алгоритма. Докажем, что всегда можно найти ответ (очередь с наибольшим числом довольных людей), в которой все довольные люди стоят вначале очереди. Предположим противное — существует позиции i и j, такие что i < j, все люди с i-го по j - 1-го недовольны, а j-тый человек доволен. Тогда просто поменяем местами людей на позиции i и j. После этого люди на с i-го по j - 1 будет по-прежнему недовольными (или некоторые станут довольными), а j-тый будет по-прежнему довольным. Таким образом, ответ не ухудшился.
Значит, нам нужно находить человека с минимальным ti, который можно обслужить сейчас и он будет доволен. Это можно сделать, отсортировав всех людей по возрастанию ti и пробуя обслуживать их по очереди. Если кто-то будет недоволен, можно отправить его в конец очереди и не добавлять время на его обслуживание к текущему времени ожидания.
Временная сложность — — O(n + sort).
Это правда, что модификация алгоритма Дейкстры, в которой среди разных расстояний выбирают то, в котором последнее ребро минимально, даёт правильный ответ.
Чтобы доказать это, немного модифицируем граф. Для начала найдём кратчайшие пути из u до каждой вершины. Обозначим через di длины кратчайшего пути из u в i. После этого можем удалить некоторые рёбра. Конкретнее, мы можем удалить ребро с концами x и y и весом w если |dx - dy| ≠ w, потому что оно не содержится ни в одном кратчайшем пути, а значит не содержится и в дереве кратчайших путей. После этого можем ориентировать рёбра от вершин с меньшим d в вершину с большим (потому что веса рёбер положительны). Легко доказать, что если взять по одному входящему ребру в каждую вершину, то эти рёбра будут образовывать дерево кратчайших путей. Тогда нам достаточно взять для каждой вершины, входящее в неё ребро минимального веса. Почему? Потому что мы должны взять хотя бы по одному ребру, входящему в каждую вершину, чтобы получить связный граф. Мы не можем взять ребра с меньшим весом, чем минимальное. И если мы возьмем минимальные рёбра мы также получим дерево кратчайших путей. Так что это и есть дерево кратчайших путей с минимальным суммарным весом.
Можно заметить, что такая модификация алгоритма Дейкстры выполняет точно такие же действия.
Time complexity —