I came across the following problem :
There is an array of size n and you are currently located at the starting point of the array, you want to go to the ending point of the array by only using steps of +3 and -1.
like if you are at x you can either go to x+3 or x-1.
The total cost of this work will be equal to the sum of the values at the indices you go through to reach the end of the array. Find the minimum cost incurred.
ex.
[4 2 1 5 6]
here the best way is 4 -> 1 -> 2 -> 6
cost = 13.
size of array <= 1e3
1 <= a[i] <= 1e3
Approach :
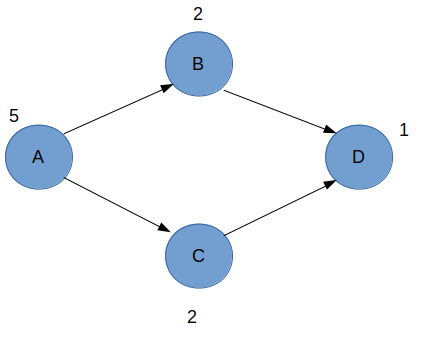
There is a DP solution for this problem, but I was wondering can it be solved by dijkshtra algorithm where we assume that index x is connect to index x+3 and x-1, taking source as 0th index and target as (n-1)th index. The magnitude of edges being the value of the node it is leading to.