vaibnak7's blog

Number of nodes reachable from each node in a directed graph
By vaibnak7, history, 4 years ago, In English

Given a directed graph, suppose we want to find the number of reachable nodes from each node of the graph then what is the best way to solve this problem ??

One obvious way to solve it is doing dfs from every node of the graph and counting how many nodes are getting visited, but the problem with this approach is that it is O(n^2) where n is the number of nodes in the graph

Then i thought of maybe if we can store at each node how many nodes are reachable and when queried give the answer based on the values of the neighbouring nodes but this will not be able to handle the case of overcounting as in the graph below.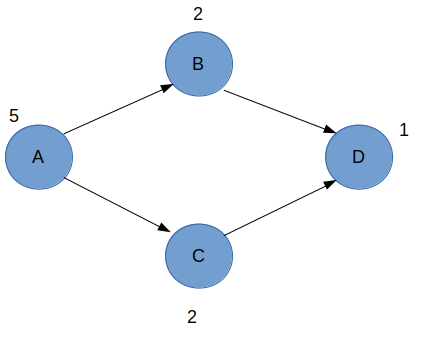

So how to solve this ?

  • Vote: I like it
  • +9
  • Vote: I do not like it

Comments Comments (20)
| Write comment?
»
4 years ago, # |
  Vote: I like it +4 Vote: I do not like it

As far as I know the question of "is it possible to solve that faster than quadratic time" is an open problem.

→ Reply
  • »
    »
    18 months ago, # ^ |
    ← Rev. 2   Vote: I like it -9 Vote: I do not like it

    If the graph is a DAG, you can just topsort and do dp.
    If not just use Kosaraju Algorithm to condense SCCs, then use topsort + dp.

    This should be linear. Or am I missing something?

    → Reply
    • »
      »
      »
      18 months ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      How would you solve the problem on a DAG using dp?

      → Reply
    • »
      »
      »
      18 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Such dp counts the number of paths starting from some vertex, but sadly there might be more than one path with the same endpoints.

      → Reply
»
4 years ago, # |
  Vote: I like it +6 Vote: I do not like it

You can optimize $$$O(n^2)$$$ with bitsets. If doing straightforward, this probably will give MLE (if n = $$$10^5$$$, ML = 256/512MB), but you can try to divide all vertices on groups, and for each group G runs separate dfs: for each vertex V count how many of vertices U(from G) are reachable from V.

→ Reply
»
4 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Spoj Problem DAGCNT2 is similar to this

→ Reply
»
2 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

This can be done by first finding Strongly Connected Components (SCC), which can be done in O(|V|+|E|). Then, build a new graph, G', where each SCC is a node in the graph and each node has value which is the sum of the nodes in that SCC.

Given a graph G(V, E), we build G'(V', E') where:

V' = { U1, U2, ..., Uk | U_i is a SCC of the graph G }

E' = { (U, W) | there is node u in U and w in W such that (u, w) is in E }

This graph, G', is a DAG and the question becomes similar with finding the number of nodes reachable from each node in a DAG, which can be made easily via DFS:

int DFS(node v) {
    vis[v] = true
    reachable[v] = v.scc_size() // nodes reachable from that SCC, including themselves

    for u in v.children() {
        // nodes already visited were added via previously visited nodes
        if (vis[u] == false) {
            reachable[v] += DFS(u)
        }
    }

    return reachable[v]
}

for v in V'  '{
    if (indegree(v) == 0) {
        DFS(v)
    }
}

So for the original nodes from G we get very easily the number of reachable nodes:

for v in V {
    reachable_G[v] = reachable[containing_scc(v)]
}

Thus the final complexity is linear O(|V| + |E|) .

→ Reply
  • »
    »
    2 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It double counts

    → Reply
    • »
      »
      »
      2 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Oh, yeah, sorry about that, it seems it doesn't cover all the cases, my bad :///

      → Reply
      • »
        »
        »
        »
        2 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        All good, Note in the case that G is a DAG, this code will calculate reachable[v] instead as the number of paths starting at node v, which can grow exponentially

        → Reply
»
18 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Basically for every node it will be n^2. So total time complexity becomes n^3 right? @author

→ Reply
  • »
    »
    18 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    No, you are doing dfs for each node so it's $$$O(n^2)$$$

    → Reply
    • »
      »
      »
      18 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Doing dfs for a single node is n^2 in the worst case where we have all nodes connected with each other. So if we do dfs for all nodes, doesn’t it make it n*n^2 = n^3?

      → Reply
      • »
        »
        »
        »
        18 months ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        dfs from one node is (n+e) afaik . multiplying by n gives of n^2

        → Reply
        • »
          »
          »
          »
          »
          18 months ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          But that e can be n^2 in worst case right. So basically if there are 5 nodes, every node can have 4 edges. So e is 20 which is close to n^2 right?

          → Reply
          • »
            »
            »
            »
            »
            »
            18 months ago, # ^ |
              Vote: I like it +14 Vote: I do not like it

            Yes but reasonable graph problems usually have m=n , but you are right. Exact time complexity is $$$O(n(n+m))$$$

            → Reply