Написал (в основном, для себя, но может быть, ещё кому-то пригодится) более подробный разбор задачи 1000D - Очередная задача на подпоследовательности, так как официальный показался мне довольно лаконичным.
Пусть на входе у нас массив чисел
1 3 1 1 1 –6 1 1
Давайте рассматривать эти числа справа налево и для каждой позиции записывать количество различных комбинаций "хороших" подпоследовательностей, которые можно построить начиная с этой позиции и до конца массива. Массив назовём sums.
Начиная с последнего числа, невозможно построить ни одной "хорошей" подпоследовательности, поэтому запишем 0.
1 3 1 1 1 –6 1 1
0
Далее, для предпоследней позиции можно получить одну "хорошую" подпоследовательность: [a7, a8]. Запишем 1.
1 3 1 1 1 –6 1 1
1 0
В шестой позиции находится число –6. Оно не может быть началом "хорошей" подпоследовательности, но если его пропустить, то далее можно построить одну уже известную нам подпоследовательность [a7, a8]. Поэтому запишем 1:
1 3 1 1 1 –6 1 1
1 1 0
Идём дальше. Следующая позиция — с номером 5, в ней находится число 1. Здесь у нас есть выбор: взять это число или пропустить его. Общее количество комбинаций "хороших" подпоследовательностей, которые можно построить начинаяя с этой позиции, будет складываться из суммы этих двух компонент. Причём вторая компонента уже известна нам — это будет значение нижнего ряда чисел для следующей позиции — числа –6. Значит, осталось определить кол-во комбинаций, если мы используем первую единичку. К единице нужно подобрать второе число. Сделать это можно тремя способами:
1 –6 ? ?
1 1 ?
1 1
При этом справа от этих вариантов остаётся пространство для манёвра: если на месте вопросиков можно собрать n комбинаций, то всего можно сделать 1 + n вариантов (n комбинаций с вопросиками и одна комбинация вообще без них). Из первой строчки получается 2 комбинации ([1, –6], [1, –6, 1, 1]), из остальных строк по одной. Итого 4 комбинации. Прибавляем к ней количество вариантов, которые можно получить, пропустив число a5 (sums6), и получаем 5:
1 3 1 1 1 –6 1 1
5 1 1 0
Далее, аналогично для a4, a3:
1 3 1 1 1 –6 1 1
23 11 5 1 1 0
Теперь нужно разобраться с a2 = 3. Попробуем действовать следующим образом. Будем фиксировать позицию a2 и позицию самого крайнего справа числа для наполнения этой тройки. Всего таких позиций 4:
3 ? ? 1 — — —
3 ? ? ? –6 — —
3 ? ? ? ? 1 —
3 ? ? ? ? ? 1
В каждой из этих позиций нужно среди вопросиков выбрать 2 числа (так как в этом хорошем массиве должно быть 3 числа, а одно — крайнее справа — мы уже зафиксировали). Определим количество вариантов выбора двух позиций из тех, что под вопросом. Например, для варианта
3 ? ? ? ? 1 —
есть 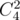 различных способов сделать это. Опять же, к каждой из получаемых таким образом комбинаций применимы все найденные прежде комбинации для позиций, оставшихся справа. Исходя из этого, мы должны сложить все
различных способов сделать это. Опять же, к каждой из получаемых таким образом комбинаций применимы все найденные прежде комбинации для позиций, оставшихся справа. Исходя из этого, мы должны сложить все 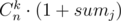 , где sumj — кол-во комбинаций для позиций справа от зафиксированного правой границы. Суммируя результат с sums4 = 23, получаем 47. Далее осталось то же самое проделать для первого элемента a1. В конечном счёте имеем
, где sumj — кол-во комбинаций для позиций справа от зафиксированного правой границы. Суммируя результат с sums4 = 23, получаем 47. Далее осталось то же самое проделать для первого элемента a1. В конечном счёте имеем
1 3 1 1 1 –6 1 1
95 47 23 11 5 1 1 0
Первый элемент получившегося массива сумм и будет ответом к задаче.
Алгоритм получился квадратичным, но нас это вполне устраивает, поскольку количество чисел не превышает 1000. Число сочетаний можно находить из треугольника Паскаля. И так как от нас требуется найти ответ по модулю 998244353, мы должны после каждого суммирования или умножения получать остаток от деления на это число (собственно, иначе бы оно и не влезло в наш 64-битный long).
Пример решения 39779763









