Problem С. Commentator problem
Let R be the distance from point А to a circle with center О and radius r. From this point the circle is observed at the angle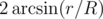 .
.So, the three stadiums are observed at the same angle if R1 / r1 = R2 / r2 = R3 / r3.
Take two different points A, B. The set of points C that AC / BC = const is either a line (perpendicular bisector of AB) or a circle with center somewhere on the line AB. This circle is easy to find. It contains two points that lie on AB and satisfy AC / BC condition.









 The results are announced - thanks to
The results are announced - thanks to 
