| Технокубок 2020 - Отборочный Раунд 1 |
|---|
| Закончено |
Назовем корректным уравнением из спичек (обозначим его как КУС) уравнение вида $$$a + b = c$$$, где все числа $$$a$$$, $$$b$$$ и $$$c$$$ целые и больше нуля.
Например, уравнения $$$2 + 2 = 4$$$ (||+||=||||) и $$$1 + 2 = 3$$$ (|+||=|||) являются КУС, а уравнения $$$1 + 2 = 4$$$ (|+||=||||), $$$2 + 2 = 3$$$ (||+||=|||) и $$$0 + 1 = 1$$$ (+|=|) — нет.
У вас есть $$$n$$$ спичек. Вы хотите составить КУС используя все ваши спички. К сожалению, возможно, что у вас не получится составить КУС, используя все ваши спички. Но вы можете докупить несколько спичек и затем собрать КУС!
Например, если $$$n = 2$$$, вы можете купить две спички и составить |+|=||, и если $$$n = 5$$$ вы можете купить одну и составить ||+|=|||.
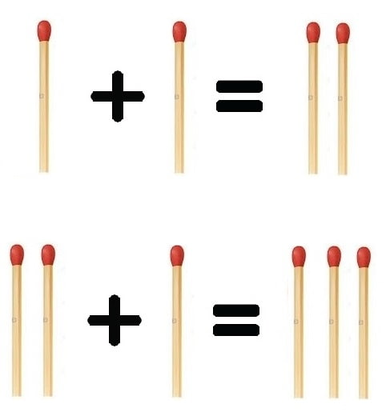
Посчитайте минимальное количество спичек, которое вам нужно купить для составления КУС.
Обратите внимание, что вам нужно ответить на $$$q$$$ независимых запросов.
Первая строка содержит одно число $$$q$$$ ($$$1 \le q \le 100$$$) — количество запросов.
Единственная строка каждого запроса содержит одно число $$$n$$$ ($$$2 \le n \le 10^9$$$) — количество спичек.
На каждый запрос выведите одно число — минимальное количество спичек, которое вам нужно купить для составления КУС.
4 2 5 8 11
2 1 0 1
Первый и второй запросы объяснены в условии.
В третьем запросе вы можете составить $$$1 + 3 = 4$$$ (|+|||=||||), не докупая спичек.
В четвертом запросе вам нужно купить одну спичку и составить $$$2 + 4 = 6$$$ (||+||||=||||||).
| Название |
|---|




