B. Omkar and Heavenly Tree
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Lord Omkar would like to have a tree with $$$n$$$ nodes ($$$3 \le n \le 10^5$$$) and has asked his disciples to construct the tree. However, Lord Omkar has created $$$m$$$ ($$$\mathbf{1 \le m < n}$$$) restrictions to ensure that the tree will be as heavenly as possible.

A tree with $$$n$$$ nodes is an connected undirected graph with $$$n$$$ nodes and $$$n-1$$$ edges. Note that for any two nodes, there is exactly one simple path between them, where a simple path is a path between two nodes that does not contain any node more than once.

Here is an example of a tree:

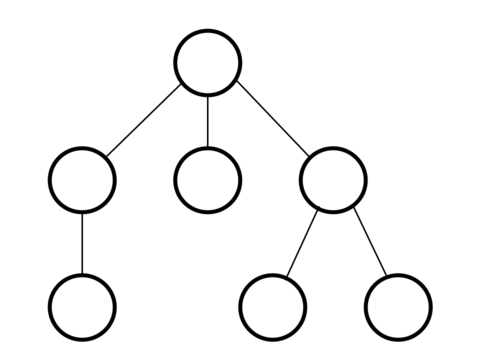
A restriction consists of $$$3$$$ pairwise distinct integers, $$$a$$$, $$$b$$$, and $$$c$$$ ($$$1 \le a,b,c \le n$$$). It signifies that node $$$b$$$ cannot lie on the simple path between node $$$a$$$ and node $$$c$$$.

Can you help Lord Omkar and become his most trusted disciple? You will need to find heavenly trees for multiple sets of restrictions. It can be shown that a heavenly tree will always exist for any set of restrictions under the given constraints.

Input

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \leq t \leq 10^4$$$). Description of the test cases follows.

The first line of each test case contains two integers, $$$n$$$ and $$$m$$$ ($$$3 \leq n \leq 10^5$$$, $$$\mathbf{1 \leq m < n}$$$), representing the size of the tree and the number of restrictions.

The $$$i$$$-th of the next $$$m$$$ lines contains three integers $$$a_i$$$, $$$b_i$$$, $$$c_i$$$ ($$$1 \le a_i, b_i, c_i \le n$$$, $$$a$$$, $$$b$$$, $$$c$$$ are distinct), signifying that node $$$b_i$$$ cannot lie on the simple path between nodes $$$a_i$$$ and $$$c_i$$$.

It is guaranteed that the sum of $$$n$$$ across all test cases will not exceed $$$10^5$$$.

Output

For each test case, output $$$n-1$$$ lines representing the $$$n-1$$$ edges in the tree. On each line, output two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) signifying that there is an edge between nodes $$$u$$$ and $$$v$$$. Given edges have to form a tree that satisfies Omkar's restrictions.

Example
Input
2
7 4
1 2 3
3 4 5
5 6 7
6 5 4
5 3
1 2 3
2 3 4
3 4 5
Output
1 2
1 3
3 5
3 4
2 7
7 6
5 1
1 3
3 2
2 4
Note

The output of the first sample case corresponds to the following tree:

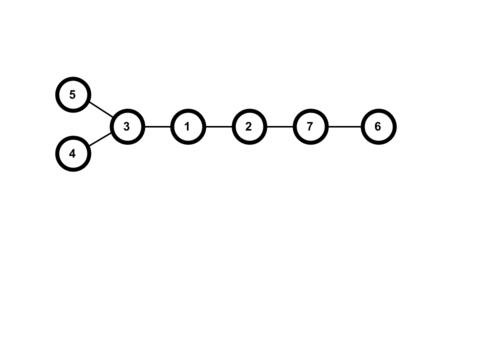
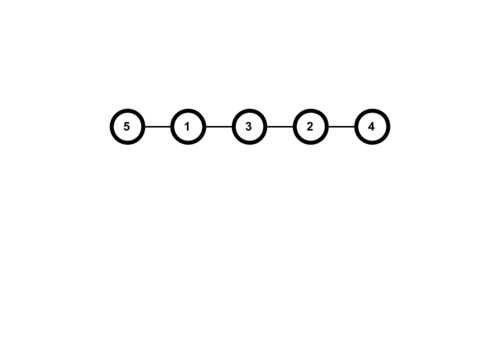
For the first restriction, the simple path between $$$1$$$ and $$$3$$$ is $$$1, 3$$$, which doesn't contain $$$2$$$. The simple path between $$$3$$$ and $$$5$$$ is $$$3, 5$$$, which doesn't contain $$$4$$$. The simple path between $$$5$$$ and $$$7$$$ is $$$5, 3, 1, 2, 7$$$, which doesn't contain $$$6$$$. The simple path between $$$6$$$ and $$$4$$$ is $$$6, 7, 2, 1, 3, 4$$$, which doesn't contain $$$5$$$. Thus, this tree meets all of the restrictions.

The output of the second sample case corresponds to the following tree: