| Технокубок 2022 - Отборочный Раунд 1 |
|---|
| Закончено |
Лорд Омкар хотел бы, чтобы у него было дерево с $$$n$$$ вершинами ($$$3 \le n \le 10^5$$$), и попросил своих учеников построить дерево. Однако Лорд Омкар создал $$$m$$$ ($$$\mathbf{1 \le m < n}$$$) ограничений, чтобы гарантировать, что дерево будет настолько божественным, насколько это возможно.
Дерево на $$$n$$$ вершинах — это связный неориентированный граф с $$$n$$$ вершинами и $$$n-1$$$ ребром. Заметим, что для любых двух вершин существует ровно один простой путь между ними, где простой путь — это путь между двумя вершинами, который не содержит ни одной вершины более одного раза.
Вот пример дерева:
Ограничение состоит из $$$3$$$ попарно различных целых чисел, $$$a$$$, $$$b$$$ и $$$c$$$ ($$$1 \le a,b,c \le n$$$). Оно означает, что вершина $$$b$$$ не может лежать на простом пути между вершинами $$$a$$$ и $$$c$$$.
Сможете ли вы помочь Лорду Омкару и стать его самым доверенным учеником? Вам нужно будет найти божественные деревья для нескольких наборов ограничений. Можно показать, что при ограничениях задачи божественное дерево всегда найдется.
Каждый тест содержит несколько наборов входных данных. Первая строка содержит количество наборов входных данных $$$t$$$ ($$$1 \leq t \leq 10^4$$$). Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$3 \leq n \leq 10^5$$$, $$$\mathbf{1 \leq m < n}$$$), представляющих размер дерева и количество ограничений.
$$$i$$$-я из следующих $$$m$$$ строк содержит три целых числа $$$a_i$$$, $$$b_i$$$, $$$c_i$$$ ($$$1 \le a_i, b_i, c_i \le n$$$, $$$a$$$, $$$b$$$, $$$c$$$ попарно различны), обозначающие, что вершина $$$b_i$$$ не может лежать на простом пути между вершинами $$$a_i$$$ и $$$c_i$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$10^5$$$
Для каждого набора входных данных выведите $$$n-1$$$ строку, обозначающих $$$n-1$$$ ребро в дереве. В каждой строке выведите два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$), обозначающие, что между вершинами $$$u$$$ и $$$v$$$ есть ребро. Данные ребра должны образовывать дерево, удовлетворяющее ограничениям Омкара.
2 7 4 1 2 3 3 4 5 5 6 7 6 5 4 5 3 1 2 3 2 3 4 3 4 5
1 2 1 3 3 5 3 4 2 7 7 6 5 1 1 3 3 2 2 4
Вывод первого набора входных данных соответствует следующему дереву:
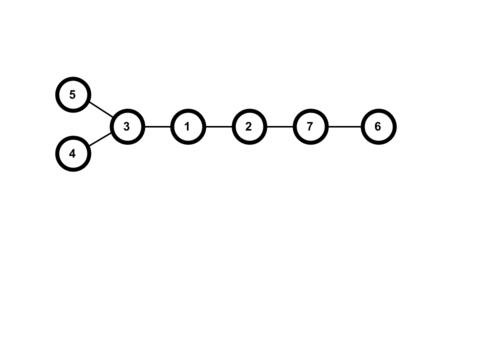
Вывод второго примера соответствует следующему дереву:
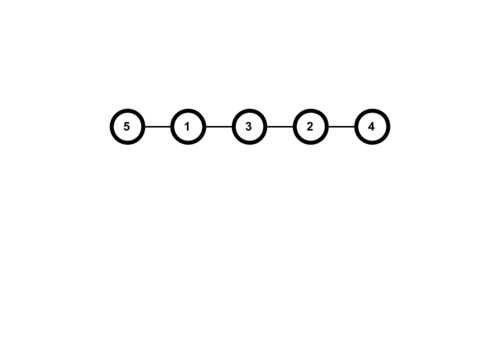
| Название |
|---|




