| VK Cup 2015 - Квалификация 2 |
|---|
| Закончено |
В этой задаче вам потребуется иметь дело с реальным алгоритмом, который используется при работе социальной сети ВКонтакте.
Как и в любой другой компании, создающей высоконагруженные сервисы, разработчикам ВКонтакте приходится регулярно иметь дело со статистикой обращений. Важным показателем, отражающим нагруженность ресурса, является среднее число запросов за некоторый промежуток времени в T секунд (например, T = 60 сек = 1 мин или T = 86400 сек = 1 сутки). Например, если это число резко падает, то это признак того, что ресурс испытывает проблемы с доступностью, а если возрастает, то это повод исследовать причины роста количества запросов, и, возможно, увеличить количество ресурсов, поддерживающих работу сервиса.
Однако даже такая естественная задача как подсчёт среднего количества запросов за промежуток времени может оказаться непростой при работе с объёмами данных, характерными для огромной социальной сети. Поэтому в процессе разработки приходится использовать оригинальные технические приёмы, позволяющие решать те или иные задачи приближённо, но при этом более эффективно.
Рассмотрим следующую формальную модель. Имеется сервис, который работает на протяжении n секунд. Нам известно количество запросов к этому ресурсу at в каждый момент времени t (1 ≤ t ≤ n). Сформулируем следующий алгоритм подсчёта среднего с экспоненциальным затуханием. Пусть c — некоторое вещественное число, строго больше единицы.
// правильной установкой этой константы можно регулировать
// промежуток времени, за который будет считаться статистика
double c = некоторая константа;
// в результате работы алгоритма эта переменная будет
// содержать среднее количество запросов за последние
// T секунд к текущему моменту времени
double mean = 0.0;
for t = 1..n: // каждую секунду делаем следующее:
// at это количество запросов, поступивших за последнюю секунду;
mean = (mean + at / T) / c;
Таким образом, переменная mean каждую секунду пересчитывается с использованием количества запросов, поступивших за эту секунду. Проведя некоторые математические выкладки можно доказать, что при правильном подборе константы c значение mean будет не сильно отличаться от реального среднего значения ax при t - T + 1 ≤ x ≤ t.
Преимущество подобного подхода заключается в том, что она использует лишь количество обращений в текущий момент времени, не требуя хранить историю запросов за большой промежуток времени. Также, она учитывает недавние значения с большим весом, чем давние, что позволяет быстрее реагировать на резкое изменение значений.
Однако перед использованием нового теоретического подхода в промышленном программировании, обязательным шагом является практическая проверка его достоверности на имеющихся тестовых наборах данных. Ваша задача — сравнить результаты, полученные в результате работы приближённого алгоритма, с настоящими значениями.
Вам даны n значений at, целое число T и вещественное число c. Также вам даны m моментов pj (1 ≤ j ≤ m), в которые нас интересует среднее значение количества запросов за последние T секунд. Реализуйте два алгоритма. Первый должен считать требуемое значение по определению, т. е. по формуле 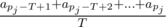 . Второй алгоритм должен считать среднее значение так, как описано выше. Выведите оба значения и посчитайте относительную ошибку второго алгоритма по формуле
. Второй алгоритм должен считать среднее значение так, как описано выше. Выведите оба значения и посчитайте относительную ошибку второго алгоритма по формуле 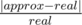 , где approx — приближённое значение, полученное вторым алгоритмом, а real — точное значение, полученное первым алгоритмом.
, где approx — приближённое значение, полученное вторым алгоритмом, а real — точное значение, полученное первым алгоритмом.
В первой строке задано целое число n (1 ≤ n ≤ 2·105), целое число T (1 ≤ T ≤ n) и вещественное число c (1 < c ≤ 100) — соответственно время работы ресурса, длина отрезка времени, в течение которого нас интересует среднее количество обращений и коэффициент c работы приближённого алгоритма. Число c задано ровно с шестью знаками после десятичной точки.
В следующей строке следуют n целых чисел at (1 ≤ at ≤ 106) — количество обращений к сервису в каждый из моментов времени.
В следующей строке записано целое число m (1 ≤ m ≤ n) — количество моментов времени, в которые нас интересует среднее количество запросов за последние T секунд.
В следующей строке следуют m целых чисел pj (T ≤ pj ≤ n), обозначающие очередной момент времени, когда нас интересует статистика. Времена pj строго возрастают.
Выведите m строк. j-я строка должна содержать три числа real, approx и error, где:
-
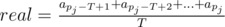 — реальное среднее количество запросов за последние T секунд;
— реальное среднее количество запросов за последние T секунд; - approx считается по приведённому алгоритму, и равняется mean в момент времени t = pj (т. е. после выполнения pj-й итерации цикла);
-
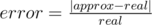 — относительная ошибка приближённого алгоритма.
— относительная ошибка приближённого алгоритма.
Выведенные вами числа будут сравниваться с правильными с относительной или абсолютной погрешностью 10 - 4. Рекомендуется выводить числа с не менее, чем пятью знаками после запятой.
1 1 2.000000
1
1
1
1.000000 0.500000 0.500000
11 4 1.250000
9 11 7 5 15 6 6 6 6 6 6
8
4 5 6 7 8 9 10 11
8.000000 4.449600 0.443800
9.500000 6.559680 0.309507
8.250000 6.447744 0.218455
8.000000 6.358195 0.205226
8.250000 6.286556 0.237993
6.000000 6.229245 0.038207
6.000000 6.183396 0.030566
6.000000 6.146717 0.024453
13 4 1.250000
3 3 3 3 3 20 3 3 3 3 3 3 3
10
4 5 6 7 8 9 10 11 12 13
3.000000 1.771200 0.409600
3.000000 2.016960 0.327680
7.250000 5.613568 0.225715
7.250000 5.090854 0.297813
7.250000 4.672684 0.355492
7.250000 4.338147 0.401635
3.000000 4.070517 0.356839
3.000000 3.856414 0.285471
3.000000 3.685131 0.228377
3.000000 3.548105 0.182702
| Название |
|---|




