| Codeforces Round 372 (Div. 1) |
|---|
| Закончено |
У Кодера ZS'а есть большое дерево. Его можно представить как неориентированный связный граф из n вершин, пронумерованных от 0 до n - 1, и n - 1 ребер между ними. На каждом ребре записана одна ненулевая цифра.
Однажды, Кодер ZS заскучал и решил исследовать некоторые параметры дерева. Он выбрал целое положительное M, которое является взаимно простым с 10, т.е. 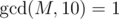 .
.
ZS считает упорядоченную пару различных вершин (u, v) интересной, когда если бы он проследовал по кратчайшему пути от вершины u до вершины v и выписывал цифры, которые он встречает на своем пути, в том же порядке, он получил бы десятичную запись целого числа, делящегося на M.
Формально, ZS считает упорядоченную пару различных вершин (u, v) интересной, если верно следующее:
- Пусть a1 = u, a2, ..., ak = v — последовательность вершин на кратчайшем пути от u до v в порядке их встречи;
- Пусть di (1 ≤ i < k) — цифра, записанная на ребре между вершинами ai и ai + 1;
- Целое число
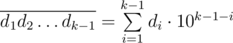 делится на M.
делится на M.
Помогите Кодеру ZS'у найти количество интересных пар!
Первая строка входных данных содержит два целых числа n и M (2 ≤ n ≤ 100 000, 1 ≤ M ≤ 109, 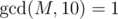 ) — количество вершин и число, которое выбрал ZS, соответственно.
) — количество вершин и число, которое выбрал ZS, соответственно.
Следующие n - 1 строк содержат по три целых числа. i-ая из них содержит ui, vi и wi, означающих ребро между вершинами ui и vi, на котором записана цифра wi (0 ≤ ui, vi < n, 1 ≤ wi ≤ 9).
Выведите единственное целое число — количество интересных (по мнению Кодера ZS'а) пар.
6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7
7
5 11
1 2 3
2 0 3
3 0 3
4 3 3
8
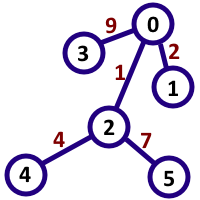
В первом примере из условия интересными являются пары (0, 4), (1, 2), (1, 5), (3, 2), (2, 5), (5, 2), (3, 5). Числа, образуемые этими парами — 14, 21, 217, 91, 7, 7, 917 соответственно, все они кратны 7. Заметьте, что (2, 5) и (5, 2) считаются различными.
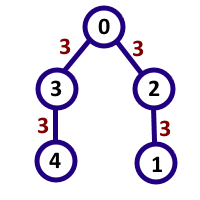
Во втором примере из условия интересными являются пары (4, 0), (0, 4), (3, 2), (2, 3), (0, 1), (1, 0), (4, 1), (1, 4), и 6 из этих пар дают число 33, а 2 из них дают число 3333, и все они кратны 11.
| Название |
|---|




