We hope everyone enjoyed the problems. Here is the editorial for the problems. I tried to make it more detailed but there might be some parts that might not be explained clearly.
Div. 2 A — Crazy Computer
Prerequisites : None
This is a straightforward implementation problem. Iterate through the times in order, keeping track of when is the last time a word is typed, keeping a counter for the number of words appearing on the screen. Increment the counter by 1 whenever you process a new time. Whenever the difference between the time for two consecutive words is greater than c, reset the counter to 0. After that, increment it by 1.
Time Complexity : O(n), since the times are already sorted.
Div. 2 B — Complete The Word
Prerequisites : None
Firstly, if the length of the string is less than 26, output - 1 immediately.
We want to make a substring of length 26 have all the letters of the alphabet. Thus, the simplest way is to iterate through all substrings of length 26 (there are O(n) such substrings), then for each substring count the number of occurrences of each alphabet, ignoring the question marks. After that, if there exist a letter that occurs twice or more, this substring cannot contain all letters of the alphabet, and we process the next substring. Otherwise, we can fill in the question marks with the letters that have not appeared in the substring and obtain a substring of length 26 which contains all letters of the alphabet. After iterating through all substrings, either there is no solution, or we already created a nice substring. If the former case appears, output - 1. Otherwise, fill in the remaining question marks with random letters and output the string.
Note that one can optimize the solution above by noting that we don't need to iterate through all 26 letters of each substring we consider, but we can iterate through the substrings from left to right and when we move to the next substring, remove the front letter of the current substring and add the last letter of the next substring. This optimization is not required to pass.
We can still optimize it further and make the complexity purely O(|s|). We use the same trick as above, when we move to the next substring, we remove the previous letter and add the new letter. We store a frequency array counting how many times each letter appear in the current substring. Additionally, store a counter which we will use to detect whether the current substring can contain all the letters of the alphabet in O(1). When a letter first appear in the frequency array, increment the counter by 1. If a letter disappears (is removed) in the frequency array, decrement the counter by 1. When we add a new question mark, increment the counter by 1. When we remove a question mark, decrement the counter by 1. To check whether a substring can work, we just have to check whether the counter is equal to 26. This solution works in O(|s|).
Time Complexity : O(|s|·262), O(|s|·26) or O(|s|)
Div. 2 C/Div. 1 A — Plus and Square Root
Prerequisites : None
Firstly, let ai(1 ≤ i ≤ n) be the number on the screen before we level up from level i to i + 1. Thus, we require all the ais to be perfect square and additionally to reach the next ai via pressing the plus button, we require 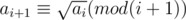 and
and 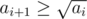 for all 1 ≤ i < n. Additionally, we also require ai to be a multiple of i. Thus, we just need to construct a sequence of such integers so that the output numbers does not exceed the limit 1018.
for all 1 ≤ i < n. Additionally, we also require ai to be a multiple of i. Thus, we just need to construct a sequence of such integers so that the output numbers does not exceed the limit 1018.
There are many ways to do this. The third sample actually gave a large hint on my approach. If you were to find the values of ai from the second sample, you'll realize that it is equal to 4, 36, 144, 400. You can try to find the pattern from here. My approach is to use ai = [i(i + 1)]2. Clearly, it is a perfect square for all 1 ≤ i ≤ n and when n = 100000, the output values can be checked to be less than 1018
Unable to parse markup [type=CF_TEX]
which is a multiple of i + 1, and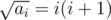 is also a multiple of i + 1.
is also a multiple of i + 1.The constraints ai must be a multiple of i was added to make the problem easier for Div. 1 A.
Time Complexity : O(n)
Div. 2 D/Div. 1 B — Complete The Graph
Prerequisites : Dijkstra's Algorithm
This problem is actually quite simple if you rule out the impossible conditions. Call the edges that does not have fixed weight variable edges. First, we'll determine when a solution exists.
Firstly, we ignore the variable edges. Now, find the length of the shortest path from s to e. If this length is < L, there is no solution, since even if we replace the 0 weights with any positive weight the shortest path will never exceed this shortest path. Thus, if the length of this shortest path is < L, there is no solution. (If no path exists we treat the length as ∞.)
Next, we replace the edges with 0 weight with weight 1. Clearly, among all the possible graphs you can generate by replacing the weights, this graph will give the minimum possible shortest path from s to e, since increasing any weight will not decrease the length of the shortest path. Thus, if the shortest path of this graph is > L, there is no solution, since the shortest path will always be > L. If no path exists we treat the length as ∞.
Other than these two conditions, there will always be a way to assign the weights so that the shortest path from s to e is exactly L! How do we prove this? First, consider all paths from s to e that has at least one 0 weight edge, as changing weights won't affect the other paths. Now, we repeat this algorithm. Initially, assign all the weights as 1. Then, sort the paths in increasing order of length. If the length of the shortest path is equal to L, we're done. Otherwise, increase the weight of one of the variable edges on the shortest path by 1. Note that this will increase the lengths of some of the paths by 1. It is not hard to see that by repeating these operations the shortest path will eventually have length L, so an assignment indeed exists.
Now, we still have to find a valid assignment of weights. We can use a similar algorithm as our proof above. Assign 1 to all variable edges first. Next, we first find and keep track of the shortest path from s to e. Note that if this path has no variable edges it must have length exactly L or strictly more than L, so either we're already done or the shortest path contains variable edges and the length is strictly less than L. (otherwise we're done)
From now on, whenever we assign weight to a variable edge (after assigning 1 to every variable edge), we call the edge assigned.
Now, mark all variable edges not on the shortest path we found as ∞ weight. (we can choose any number greater than L as ∞) Next, we will find the shortest path from s to e, and replace the weight of an unassigned variable edge such that the length of the path becomes equal to L. Now, we don't touch the assigned edges again. While the shortest path from s to e is still strictly less than L, we repeat the process and replace a variable edge that is not assigned such that the path length is equal to L. Note that this is always possible, since otherwise this would've been the shortest path in one of the previous steps. Eventually, the shortest path from s to e will have length exactly L. It is easy to see that we can repeat this process at most n times because we are only replacing the edges which are on the initial shortest path we found and there are less than n edges to replace (we only touch each edge at most once). Thus, we can find a solution after less than n iterations. So, the complexity becomes 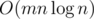 . This is sufficient to pass all tests.
. This is sufficient to pass all tests.
What if the constraints were n, m ≤ 105? Can we do better?
Yes! Thanks to HellKitsune who found this solution during testing. First, we rule out the impossible conditions like we did above. Then, we assign all the variable edges with ∞ weight. We enumerate the variable edges arbitarily. Now, we binary search to find the minimal value p such that if we make all the variable edges numbered from 1 to p have weight 1 and the rest ∞, then the shortest path from s to e has length ≤ L. Now, note that if we change the weight of p to ∞ the length of shortest path will be more than L. (if p equals the number of variable edges, the length of the shortest path is still more than L or it will contradict the impossible conditions) If the weight is 1, the length of the shortest path is ≤ L. So, if we increase the weight of edge p by 1 repeatedly, the length of the shortest path from s to e will eventually reach L, since this length can increase by at most 1 in each move. So, since the length of shortest path is non-decreasing when we increase the weight of this edge, we can binary search for the correct weight. This gives an 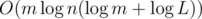 solution.
solution.
Time Complexity : 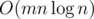 or
or 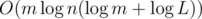
Div. 2 E/Div. 1 C — Digit Tree
Prerequisites : Tree DP, Centroid Decomposition, Math
Compared to the other problems, this one is more standard. The trick is to first solve the problem if we have a fixed vertex r as root and we want to find the number of paths passing through r that works. This can be done with a simple tree dp. For each node u, compute the number obtained when going from r down to u and the number obtained when going from u up to r, where each number is taken modulo M. This can be done with a simple dfs. To calculate the down value, just multiply the value of the parent node by 10 and add the value on the edge to it. To calculate the up value, we also need to calculate the height of the node. (i.e. the distance from u to r) Then, if we let h be the height of u, d be the digit on the edge connecting u to its parent and val be the up value of the parent of u, then the up value for u is equal to 10h - 1·d + val. Thus, we can calculate the up and down value for each node with a single dfs.
Next, we have to figure out how to combine the up values and down values to find the number of paths passing through r that are divisible by M. For this, note that each path is the concatenation of a path from u to r and r to v, where u and v are pairs of vertices from different subtrees, and the paths that start from r and end at r. For the paths that start and end at r the answer can be easily calculated with the up and down values (just iterate through all nodes as the other endpoint). For the other paths, we iterate through all possible v, and find the number of vertices u such that going from u to v will give a multiple of M. Since v is fixed, we know its height and down value, which we denote as h and d respectively. So, if the up value of u is equal to up, then up·10h + d must be a multiple of M. So, we can solve for up to be - d·10 - h modulo M. Note that in this case the multiplicative inverse of 10 modulo M is well-defined, as we have the condition 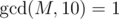 . To find the multiplicative inverse of 10, we can find φ(M) and since by Euler's Formula we have xφ(M) ≡ 1(modM) if
. To find the multiplicative inverse of 10, we can find φ(M) and since by Euler's Formula we have xφ(M) ≡ 1(modM) if 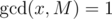 , we have xφ(M) - 1 ≡ x - 1(modM), which is the multiplicative inverse of x (in this case we have x = 10) modulo M. After that, finding the up value can be done by binary exponentiation.
, we have xφ(M) - 1 ≡ x - 1(modM), which is the multiplicative inverse of x (in this case we have x = 10) modulo M. After that, finding the up value can be done by binary exponentiation.
Thus, we can find the unique value of up such that the path from u to v is a multiple of M. This means that we can just use a map to store the up values of all nodes and also the up values for each subtree. Then, to find the number of viable nodes u, find the required value of up and subtract the number of suitable nodes that are in the same subtree as v from the total number of suitable nodes. Thus, for each node v, we can find the number of suitable nodes u in 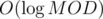 time.
time.
Now, we have to generalize this for the whole tree. We can use centroid decomposition. We pick the centroid as the root r and find the number of paths passing through r as above. Then, the other paths won't pass through r, so we can remove r and split the tree into more subtrees, and recursively solve for each subtree as well. Since each subtree is at most half the size of the original tree, and the time taken to solve the problem where the path must pass through the root for a single tree takes time proportional to the size of the tree, this solution works in 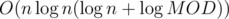 time, where the other
time, where the other  comes from using maps.
comes from using maps.
Time Complexity : 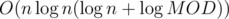
Div. 1 D — Create a Maze
Prerequisites : None
The solution to this problem is quite simple, if you get the idea. Thanks to danilka.pro for improving the solution to the current constraints which is much harder than my original proposal.
Note that to calculate the difficulty of a given maze, we can just use dp. We write on each square (room) the number of ways to get from the starting square to it, and the number written on (i, j) will be the sum of the numbers written on (i - 1, j) and (i, j - 1), and the edge between (i - 1, j) and (i, j) is blocked, we don't add the number written on (i - 1, j) and similarly for (i, j - 1). We'll call the rooms squares and the doors as edges. We'll call locking doors as edge deletions.
First, we look at several attempts that do not work.
Write t in its binary representation. To solve the problem, we just need to know how to construct a maze with difficulty 2x and x + 1 from a given maze with difficulty x. The most direct way to get from x to 2x is to increase both dimensions of the maze by 1. Let's say the bottom right square of the grid was (n, n) and increased to (n + 1, n + 1). So, the number x is written at (n, n). Then, we can block off the edge to the left of (n + 1, n) and above (n, n + 1). This will make the numbers in these two squares equal to x, so the number in square (n + 1, n + 1) would be 2x, as desired. To create x + 1 from x, we can increase both dimensions by 1, remove edges such that (n + 1, n) contains x while (n, n + 1) contains 1 (this requires deleting most of the edges joining the n-th column and (n + 1)-th column. Thus, the number in (n, n) would be x + 1. This would've used way too many edge deletions and the size of the grid would be too large. This was the original proposal.
There's another way to do it with binary representation. We construct a grid with difficulty 2x and 2x + 1 from a grid with difficulty x. The key idea is to make use of surrounding 1s and maintaining it with some walls so that 2x + 1 can be easily constructed. This method is shown in the picture below. This method would've used around 120 × 120 grid and 480 edge deletions, which is too large to pass.
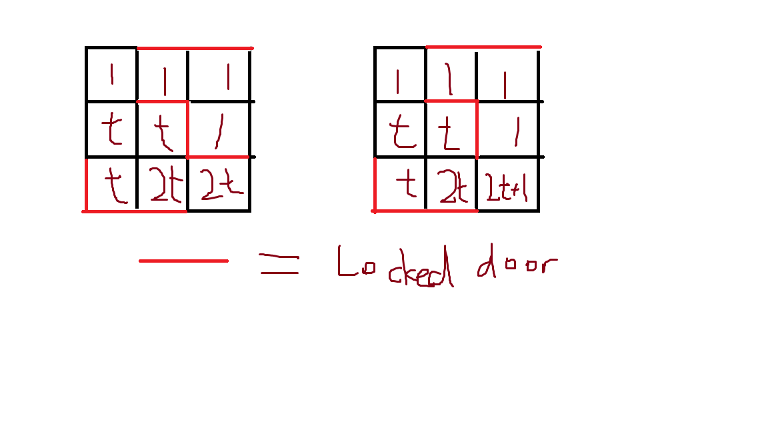
Now, what follows is the AC solution. Since it's quite easy once you get the idea, I recommend you to try again after reading the hint. To read the full solution, click on the spoiler tag.
Hint : Binary can't work since there can be up to 60 binary digits for t and our grid size can be at most 50. In our binary solution we used a 2 × 2 grid to multiply the number of ways by 2. What about using other grid sizes instead?
Of course, this might not be the only way to solve this problem. Can you come up with other ways of solving this or reducing the constraints even further? (Open Question)
Time Complexity : 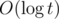
Div. 1 E — Complete The Permutations
Prerequisites : Math, Graph Theory, DP, Any fast multiplication algorithm
We'll slowly unwind the problem and reduce it to something easier to count. First, we need to determine a way to tell when the distance between p and q is exactly k. This is a classic problem but I'll include it here for completeness.
Let f denote the inverse permutation of q. So, the minimum number of swaps to transform p into q is the minimum number of swaps to transform pfi into the identity permutation. Construct the graph where the edges are 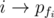 for all 1 ≤ i ≤ n. Now, note that the graph is equivalent to
for all 1 ≤ i ≤ n. Now, note that the graph is equivalent to  and is composed of disjoint cycles after qi and pi are filled completely. Note that the direction of the edges doesn't matter so we consider the edges to be
and is composed of disjoint cycles after qi and pi are filled completely. Note that the direction of the edges doesn't matter so we consider the edges to be 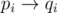 for all 1 ≤ i ≤ n. Note that if the number of cycles of the graph is t, then the minimum number of swaps needed to transform p into q would be n - t. (Each swap can break one cycle into two) This means we just need to find the number of ways to fill in the empty spaces such that the number of cycles is exactly i for all 1 ≤ i ≤ n.
for all 1 ≤ i ≤ n. Note that if the number of cycles of the graph is t, then the minimum number of swaps needed to transform p into q would be n - t. (Each swap can break one cycle into two) This means we just need to find the number of ways to fill in the empty spaces such that the number of cycles is exactly i for all 1 ≤ i ≤ n.
Now, some of the values pi and qi are known. The edges can be classified into four types :
A-type : The edges of the form 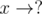 , i.e. pi is known, qi isn't.
, i.e. pi is known, qi isn't.
B-type : The edges of the form 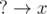 , i.e. qi is known, pi isn't.
, i.e. qi is known, pi isn't.
C-type : The edges of the form  , i.e. both pi and qi are known.
, i.e. both pi and qi are known.
D-type : The edges of the form 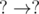 , i.e. both pi and qi are unknown.
, i.e. both pi and qi are unknown.
Now, the problem reduces to finding the number of ways to assign values to the question marks such that the number of cycles of the graph is exactly i for all 1 ≤ i ≤ n. First, we'll simplify the graph slightly. While there exists a number x appears twice (clearly it can't appear more than twice) among the edges, we will combine the edges with x together to simplify the graph. If there's an edge  , then we increment the total number of cycles by 1 and remove this edge from the graph. If there is an edge
, then we increment the total number of cycles by 1 and remove this edge from the graph. If there is an edge  and
and 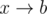 , where a and b might be some given numbers or question marks, then we can merge them together to form the edge
, where a and b might be some given numbers or question marks, then we can merge them together to form the edge 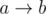 . Clearly, these are the only cases for x to appear twice. Hence, after doing all the reductions, we're reduced to edges where each known number appears at most once, i.e. all the known numbers are distinct. We'll do this step in O(n2). For each number x, store the position i such that pi = x and also the position j such that qj = x, if it has already been given and - 1 otherwise. So, we need to remove a number when the i and j stored are both positive. We iterate through the numbers from 1 to n. If we need to remove a number, we go to the two positions where it occur and replace the two edges with the new merged one. Then, recompute the positions for all numbers (takes O(n) time). So, for each number, we used O(n) time. (to remove naively and update positions) Thus, the whole complexity for this part is O(n2). (It is possible to do it in O(n) with a simple dfs as well. Basically almost any correct way of doing this part that is at most O(n3) works, since the constraints for n is low)
. Clearly, these are the only cases for x to appear twice. Hence, after doing all the reductions, we're reduced to edges where each known number appears at most once, i.e. all the known numbers are distinct. We'll do this step in O(n2). For each number x, store the position i such that pi = x and also the position j such that qj = x, if it has already been given and - 1 otherwise. So, we need to remove a number when the i and j stored are both positive. We iterate through the numbers from 1 to n. If we need to remove a number, we go to the two positions where it occur and replace the two edges with the new merged one. Then, recompute the positions for all numbers (takes O(n) time). So, for each number, we used O(n) time. (to remove naively and update positions) Thus, the whole complexity for this part is O(n2). (It is possible to do it in O(n) with a simple dfs as well. Basically almost any correct way of doing this part that is at most O(n3) works, since the constraints for n is low)
Now, suppose there are m edges left and p known numbers remain. Note that in the end when we form the graph we might join edges of the form 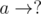 and
and  (where a and b are either fixed numbers or question marks) together. So, the choice for the ? can be any of the m - p remaining unused numbers. Note that there will be always m - p such pairs so we need to multiply our answer by (m - p)! in the end. Also, note that the ? are distinguishable, and order is important when filling in the blanks.
(where a and b are either fixed numbers or question marks) together. So, the choice for the ? can be any of the m - p remaining unused numbers. Note that there will be always m - p such pairs so we need to multiply our answer by (m - p)! in the end. Also, note that the ? are distinguishable, and order is important when filling in the blanks.
So, we can actually reduce the problem to the following : Given integers a, b, c, d denoting the number of A-type, B-type, C-type, D-type edges respectively. Find the number of ways to create k cycles using them, for all 1 ≤ k ≤ n. Note that the answer is only dependent on the values of a, b, c, d as the numbers are all distinct after the reduction.
First, we'll look at how to solve the problem for k = 1. We need to fit all the edges in a single cycle. First, we investigate what happens when d = 0. Note that we cannot have a B-type and C-type edge before an A-type or C-type edge, since all numbers are distinct so these edges can't be joined together. Similarly, an A or C-type edge cannot be directly after a B or C-type edge. Thus, with these restrictions, it is easy to see that the cycle must contain either all A-type edges or B-type edges. So, the answer can be easily calculated. It is also important to note that if we ignore the cyclic property then a contiguous string of edges without D must be of the form AA...BB.. or AA...CBB..., where there is only one C, and zero or more As and Bs.
Now, if d ≥ 1, we can fix one of the D-type edges as the front of the cycle. This helps a lot because now we can ignore the cyclic properties. (we can place anything at the end of the cycle because D-type edges can connect with any type of edges) So, we just need to find the number of ways to make a length n - 1 string with a As, b Bs, c Cs and d - 1 Ds. In fact, we can ignore the fact that the A-type edges, B-type edges, C-type edges and D-type edges are distinguishable and after that multiply the answer by a!b!c!(d - 1)!.
We can easily find the number of valid strings we can make. First, place all the Ds. Now, we're trying to insert the As, Bs and Cs into the d empty spaces between, after and before the Ds. The key is that by our observation above, we only care about how many As, Bs and Cs we insert in each space since after that the way to put that in is uniquely determined. So, to place the As and Bs, we can use the balls in urns formula to find that the number of ways to place the As is 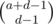 and the number of ways to place the Bs is
and the number of ways to place the Bs is 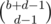 . The number of ways to place the Cs is
. The number of ways to place the Cs is 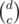 , since we choose where the Cs should go.
, since we choose where the Cs should go.
Thus, it turns out that we can find the answer in O(1) (with precomputing binomial coefficients and factorials) when k = 1. We'll use this to find the answer for all k. In the general case, there might be cycles that consists entirely of As and entirely of Bs, and those that contains at least one D. We call them the A-cycle, B-cycle and D-cycles respectively.
Now, we precompute f(n, k), the number of ways to form k cycles using n distinguishable As. This can be done with a simple dp in O(n3). We iterate through the number of As we're using for the first cycle. Then, suppose we use m As. The number of ways to choose which of the m As to use is 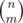 and we can permute them in (m - 1)! ways inside the cycle. (not m! because we have to account for all the cyclic permutations) Also, after summing this for all m, we have to divide the answer by k, to account for overcounting the candidates for the first cycle (the order of the k cycles are not important)
and we can permute them in (m - 1)! ways inside the cycle. (not m! because we have to account for all the cyclic permutations) Also, after summing this for all m, we have to divide the answer by k, to account for overcounting the candidates for the first cycle (the order of the k cycles are not important)
Thus, f(n, k) can be computed in O(n3). First, we see how to compute the answer for a single k. Fix x, y, e, f, the number of A-cycles, B-cycles, number of As in total among the A-cycles and number of Bs in total among the B-cycles. Then, since k is fixed, we know that the number of D-cycles is k - x - y. Now, we can find the answer in O(1). First, we can use the values of f(e, x), f(f, y), f(d, k - x - y) to determine the number of ways to place the Ds, and the As, Bs that are in the A-cycles and B-cycles. Then, to place the remaining As, Bs and Cs, we can use the same method as we did for k = 1 in O(1), since the number of spaces to place them is still the same. (You can think of it as each D leaves an empty space to place As, Bs and Cs to the right of it) After that, we multiply the answer by 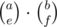 to account for the choice of the set of As and Bs used in the A-only and B-only cycles. Thus, the complexity of this method is O(n4) for each k and O(n5) in total, which is clearly too slow.
to account for the choice of the set of As and Bs used in the A-only and B-only cycles. Thus, the complexity of this method is O(n4) for each k and O(n5) in total, which is clearly too slow.
We can improve this by iterating through all x + y, e, f instead. So, for this to work we need to precompute f(e, 0)f(f, x + y) + f(e, 1)f(f, x + y - 1) + ... + f(e, x + y)f(f, 0), which we can write as g(x + y, e, f). Naively doing this precomputation gives O(n4). Then, we can calculate the answer by iterating through all x + y, e, f and thus getting O(n3) per query and O(n4) for all k. This is still too slow to pass n = 250.
We should take a closer look of what we're actually calculating. Note that for a fixed pair e, f, the values of g(x + y, e, f) can be calculated for all possible x + y in  or O(n1.58) by using Number Theoretic Transform or Karatsuba's Algorithm respectively. (note that the modulus has been chosen for NFT to work) This is because if we fix e, f, then we're precisely finding the coefficients of the polynomial (f(e, 0)x0 + f(e, 1)x1 + ... + f(e, n)xn)(f(f, 0)x0 + f(f, 1)x1 + ... + f(f, n)xn), so this can be handled with NFT/Karatsuba.
or O(n1.58) by using Number Theoretic Transform or Karatsuba's Algorithm respectively. (note that the modulus has been chosen for NFT to work) This is because if we fix e, f, then we're precisely finding the coefficients of the polynomial (f(e, 0)x0 + f(e, 1)x1 + ... + f(e, n)xn)(f(f, 0)x0 + f(f, 1)x1 + ... + f(f, n)xn), so this can be handled with NFT/Karatsuba.
Thus, the precomputation of g(x + y, e, f) can be done in 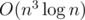 or O(n3.58).
or O(n3.58).
Next, suppose we fixed e and f. We will calculate the answer for all possible k in  similar to how we calculated g(x + y, e, f). This time, we're multiplying the following two polynomials : f(d, 0)x0 + f(d, 1)x1 + ... + f(d, n)xn and g(0, e, f)x0 + g(1, e, f)x1 + ... + g(n, e, f)xn. Again, we can calculate this using any fast multiplication method, so the entire solution takes
similar to how we calculated g(x + y, e, f). This time, we're multiplying the following two polynomials : f(d, 0)x0 + f(d, 1)x1 + ... + f(d, n)xn and g(0, e, f)x0 + g(1, e, f)x1 + ... + g(n, e, f)xn. Again, we can calculate this using any fast multiplication method, so the entire solution takes 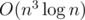 or O(n3.58), depending on which algorithm is used to multiply polynomials.
or O(n3.58), depending on which algorithm is used to multiply polynomials.
Note that if you're using NFT/FFT, there is a small trick that can save some time. When we precompute the values of g(x + y, e, f), we don't need to do inverse FFT on the result and leave it in the FFTed form. After that, when we want to find the convolution of f(d, i) and g(i, e, f), we just need to apply FFT to the first polynomial and multiply them. This reduces the number of FFTs and it reduced my solution runtime by half.
Time Complexity : 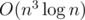 or O(n3.58), depending on whether NFT or Karatsuba is used.
or O(n3.58), depending on whether NFT or Karatsuba is used.










Very nice problem set. Hope to see you prepare more rounds in the future!
Ya, I hope so. Currently this is the last of my problems for now but maybe there'll be more in the future.
Hey, the O(mnlogn) approach gave TLE on case 127 during contest, replacing cin/cout by scanf printf passed all test cases. Why are such cases kept? :/
20710181
Because you should know that cin/cout is much slower unless "desynced": adding
speeds cin/cout up to be roughly as fast as scanf/printf.
Really fast editorial. This is how all editorials should be written :)
Sorry. I was wrong. nice editorial :)
My idea for Div1 D (which unfortunately didn't pass because I miscounted something crucial) was to use base 70.
Each digit is constructed with a hard-coded solution. The rest of the walls are shown above.
You might notice that each digit is a 6x5 area and not 5x5. Turns out that with 5x5, there is no grid giving exactly 67 paths. Had 5x5 worked, my idea would have also worked... almost. It needed 301 walls.
EDIT: You might notice that I did make a submission implementing this idea. When I first counted it, I forgot to account the last x70 block, so I thought I only needed 296 walls.
This is not very important, but for the first sample solution for 716B - Complete the Word, should the time complexity be O(26 * 2 * |s|) and not O(262 * |s|) ? Anyway, thank you for writing a detailed editorial and providing solution code as well!
"Now, we binary search to find the maximal value p such that if we make all the variable edges numbered from 1 to p have weight 1 and the rest ∞, then the shortest path from s to e has length ≤ L. "
This should be minimal, right? It confused me for a while while reading the editorial.
You're right, I'll correct it.
Did authors expect "random walking" as solution in D? (start with empty grid, add some walls, while answer is enough big... start again).
If yes, what is running time of author's implementation?
My "random walking" has got TL 161 during the contest.
After optimization in 1.5 times, it gets OK in 1.3 sec =(
Nope, we were not expected that. Honestly, we should have set the TL to 0.5s to avoid this, but we just had not realized that such kind of solutions will do fine.
We'll be patient next time ;)
My "not-random walking", i.e. on every step take the wall which will maximally reduce number of ways from (1,1) to (n,m), but still be >= T, pass in 0.187 secs:
Submission
I could AC it during contest, but forgot how to recalculate answer in O(1) when we add one wall to current field and done it using N*M recalculation.
Amazing it works...
Am I the only one stuck finding a relation in Div2C ? :(
Here is a my method of solving Div2 C: I just wrote a really slow solution. I wrote it down on paper and tried to found consistent pattern. To be honest, I do not know why my solution works but it got "ACCEPTED".
So was I during the contest, so I tried to brute it in a slightly optimised way :) That's an alternative to O(n). Although it's incredibly slow. http://codeforces.net/contest/716/submission/20703268
i made it as a picture so it can be more readable since some how the comment don't deal with my enters :D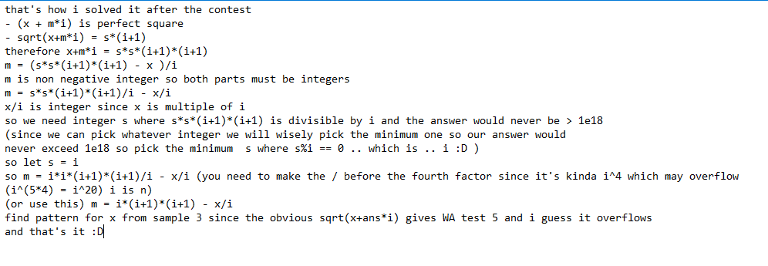
My cenroid decomposition is exactly O(nlogn), gets OK in 0.343 sec.
Use hash map
Inverse? Precalculate all negative powers of 10.
Ya you're right. Indeed these optimizations will make it .
.
Can anybody explain why
I got TLE using unordered_map http://codeforces.net/contest/715/submission/20724049
But got AC using map http://codeforces.net/contest/716/submission/20703268
Isn't unordered_map faster than map? Maybe the clear operations slows down the unordered_map?
unordered_map can be hacked. See this: https://ipsc.ksp.sk/2014/real/problems/h.html
Thanks!
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
I have a faster (and easier to code!) solution for Div1B. It's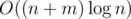 . I described it in this comment!
. I described it in this comment!
I have a cool Div1D Solution!
I used power of 3. with this structure, we only need to calculate the digit values of T in base of 3. if a digit is "0", we close all the blue and green "doors" for that digit. if a digit is "1", we open one "door". if a digit is "2", we open both doors. it gives a 41 * 41 size board (since ceil(log3(10^18)) == 38 and we need some more outlines) and max 299 walls. but we can remove some more walls at the outside.
Source : here
nice problemset and well_written editorial hope to see your next round
You was not expected O(n4) solution to pass (in E)? 20714654 Really?
I'm confident that for n < 250 O(n2) multiplication is faster than FFT.
Yep, you're right that we were not expected O(n4) to pass. Actually we had one solution in O(n4) that appears to be written in very unoptimal way.
Anyway, great job getting the solution accepted!, we hoped you'll get an AC during the contest.
Thanks for the great problem, I enjoyed it a lot. Also thanks for
nastynot to my taste problem C which forced me to solve E :) (no offence just don't like this kind of problems)We can find inverse of 10 mod m in O(10) :P. We need a, b, so that a * 10 + b * m = 1. We iterate through b and check if bm mod 10 is 1 and if yes then we get a :P. Either way, I used exgcd during contest xD.
Problem B div1: Complete The Graph, can be solved simply in O(n + m * log(m)).
First, let all the erased edges be weighted 1.
Then, run dijkstra from t, and save for each node its shortest distance from t.
Then, run dijkstra from s, and if the current edge is erased, then let its weight be = max( 1, L — current distance — shortest distance from the other end of the edge to t).
If at the end the shortest path from s to t was L, then there's an answer, which was formed during the second dijkstra. So the solution is simply running dijkstra twice.
Proof:-
-- If it's currently not a shortest path edge, you do nothing.
-- If it's but the shortest path is < L, you modify this edge to make the path through it = L. By modifying the current edge you are sure that you're modifying a path distance to be = L, and no other edge weight in this path will modified in the future, unless there'll be another path distance = L. And you never let a path distance < L unless it has no erased edges. In that case it's impossible anyway, else you end up with at least one path distance = L, and the shortest distance >= L, so the shortest distance = L.
Code: 20710911
Thanks for the logic. I solved Div2D finally after so many wa's. All thanks to U.
Also learnt that Priority Queue is slow in Java . So rather Use TreeSet
http://codeforces.net/contest/716/submission/20731857 I got TLE IN TESTCASE 117 . Next i replaced PriorityQueue in JAva and used TreeSet http://codeforces.net/contest/716/submission/20732812
Bamm and its Accepted. It was fun.
This is an awesome solution! Thanks.
Edit: How will it handle the cases if the edges are repeating? Like, if there is a corner vertice with only one edge to main part of the graph, so if dijkstraS changes that edge value, it won't reflect in distT, hence the same edge gets different values.
This is Awesome!! Thank You :)
Hello, I got WA in systests of Div 2 B. Could somebody kindly point out the mistake?
http://codeforces.net/contest/716/submission/20692380
About problem "Complete The Graph ": In my country, 0 is considered positive by some people. Even the math teachers have different opinions because we also use the term "strictly positive" for numbers > 0. Does "positive" always mean ">0" in English?
Yeah, it always does. Maybe you're confused because 0 is sometimes considered a natural number? It surely is not positive though.
In Div2-D/Div1-B, is there a way to solve the problem by modelling it as a minCost-maxFlow problem? I was trying this approach throughout the contest but couldn't find a way to do it.
Also, naming the starting as "s" and ending as "t" made me think of it as "source" and the "sink" since thats the commonly used variables for them. Even though I thought about a solution with Dijkstra, this made me continue to look at it as flow problem!
In problem DIV2-D/DIV1-B, I solved it by excluding invalid cases as described in the editorial, then I run Dijkstra to find the shortest path from s to t (with replacing missing edges with ones).
After that I increase only ONE variable edge on the shortest path to a value that makes that shortest path equals to L. I assign infinity to all other variable edges.
I'm still getting wrong answer with this solution :( Is there anything wrong with this approach?
http://codeforces.net/contest/716/submission/20718122
Maybe now there is other shorter path then your edge. Sometimes you cannot set this value.
5 5 4 0 4
0 1 0
1 2 1
1 3 1
3 4 0
2 4 1
it's clearly wrong in this input if you just assign 2 to the fourth edge , and 1 to the first one.
in the explanation of the problem C-div2 it is written that:
"we also require ai to be a multiple of i", why ?
Not sure I'm a fan of extremely tight constraints for a constructive problem such as D. The intended solution itself needs exactly 50x50 space (and nearly exactly 300 walls), so you're leaving very few room for creativity in solutions.
Though my own case wasn't a problem with creativity; I saw the base 6 idea during the contest, but didn't eliminate the exterior walls, so I spent 320 walls instead of 300. Commenting two lines of the solution makes it pass :(
Can't agree more. I wanted to write exactly same comment after solving it today. Fortunately I didn't encounter problems with that, but I imagined how mad I would be if it had turned out I use 310 walls or something.
Editorial for Div2 D says
Firstly, we ignore the variable edges. Now, find the length of the shortest path from s to e. If this length is < L, there is no solutionI don't understand why there's no solution, as all paths from s to e can contain some of the variable edges, making it possible. What did I not understand?
We want the shortest path to have length L. Since the shortest path in this case does not pass through any variable edges and is already shorter than L, there is nothing we can do to increase its length. Hence we can never set the shortest path to L and there is no solution.
I understand now.
In what cases should I expect unordered_map to be slower than normal map? I am quite confused as I haven't encountered this before, I always assumed unordered_map would be OK.
unordered_map TLE: 20721642 map AC: 20722164
I would really appreciate any insight on this! Thanks in advance.
maybe rehash
[D. Complete The Graph] why don't we assign all unknown edge with value=0, then find the shortest path, and if the shortest path was under value = p, then it is impossible to find solution, else we check the shortest path and assign the unkown edge to make the path length = p, and set the rest of the unknown edges to infinity ?????????????
take this case : 5 5 4 0 4
0 1 0
1 2 1
1 3 1
3 4 0
2 4 1
it's clearly wrong in this input either if you just assign 2 to the fourth edge and 1 to the first one,or if you assign 2 to the fourth edge and oo to the first one
Div 1 D:
My solution 20712414 uses 50 rows and 36 columns
Block 1: 31 rows x 35 columns (1620288010530347424)
Block 2: 15 rows x 35 columns (482320623240)
Block 3: 4 rows x 35 columns (7770)
As you can see if there are only red walls we have 64C34 + 48C34 + 37C34 = 1620288010530347424 + 482320623240 + 7770 ways.
Now the walls on the blue lines can be deleted independently to reduce the answer. After sorting the values are like this: 1, 1, 1, 3, 6, 10, 14, 15, 21, 28, ..., 191724747789809255, 218169540588403635, 409894288378212890, 409894288378212890. This (multi)set of numbers is able to produce any subset sum between 1 and 10^18.
Max number of walls is 261 when input = 3.
Wondering how you find to divide the room like this? Did you write another code to find it?
I had an alternative solution for Div 1 C, also either O(n log n) or O(n log n log n) depending on whether you use a hash table or balanced binary tree. I couldn't make it work during the contest (today I discovered that multiset::count can take O(log n + count(k)) time, not just O(log n)), but I made it work afterwards.
Consider the tree to be rooted. For each subtree, we will compute the following, recursively:
This can be done by tree DP: for a particular subtree root, merge in the children one at a time. The problem is that done naively, this can be O(n^2) for a very deep tree. There are two tricks necessary to make this O(n log n):
The second condition means that each time a value is used in iteration, it goes into a list that is at least twice the size. Thus, it is iterated only O(log n) times.
I used this approach at first but I found that I didn't know how to add an extra down edge. How do you do that? Edit: Another problem I met is I don't know how to count the suffixes which match a given prefix.
Edit: Sorry, I didn't notice that you store something different in your second list. Now I understand :P
wrong answer on test 5(also where can i find the test cases?) for Div2 C
20728168
Could someone please tell what is wrong with the code.
It's the overflow bug.
I am no expert with Java, but (int) should hold only about 2e9, while the power of pow could be 1e16.
Integer Overflow.
Could you tell me what is the trick in Div.2 E's test 119?
http://codeforces.net/contest/716/submission/20732311
Thanks so much !!!
(I'm new here and it's a pity to see WA 119 while there're 120 test cases.
dear zscoder:in CF716B_Complete the Word,your Code O(26^2*|s|) is O(26*|s|)actually.
phi(M) is not required to find inverse of 10. Just check M+1, 2M+1, ... 9M+1 one of these can be divided by 10.
Hi everyone in the editorial of div2/d div1/b ,I didn't understand why this is true: "It is easy to see that we can repeat this process at most n times because we are only replacing the edges which are on the initial shortest path we found and there are less than n edges to replace ". I mean why there are at most n edges to replace in the shortest paths graph. could anyone explain that in details. thanks in advance;
same doubt
There are n vertices in a graph and the shortest way doesn't visit any vertex twice. So at most the algorithm visits n vertices and n-1 edges.
in Div2 D: what is wrong with this approach:
replace all erased edges with cost 1, then find the shortest path (let us call it 'len'), then go through every edge in the shortest path, change the cost of the first erased edge you find to be L-len+1, then go to the erased edges that is not on the shortest path and set there cost to infinity, then add the changes to the original graph, then find the shortest path again, if the length of the path is not L, print 'NO', otherwise print the solution.
the source code: 20740319
take this case :
5 5 4 0 4
0 1 0
1 2 1
1 3 1
3 4 0
2 4 1
in this case : if the fourth edge is the first one u meet in ur dijkstra , u will assign 2 to it and assign 1 to the first one , then ur ans will be NO , because there still a path shorter than L;
To solve your problem, find the shortest path s to t, and instead of setting the value of the first variable edge equals to the L-len+1, you can do a binary search(lower bound) on the new value of the variable edges, and if the path is less than L, adds in the value of the first variable edge of the shortest path, the amount needed for the shortest path be equal to L. Then check if the length of the path is L.
My approach: 20754984
ignore
Is there a simpler solution to the Div2 D/Div1 B?
Here's a O(n2) solution for 715E - Complete the Permutations.
Consider pi as an edge from (i, 1) to (pi, 0), qi as an edge from (i, 0) to (qi, 1).
There exists four kinds of chains : 01, 10, 11, 00, (e.g. 01 means (x,0)->....->(y,1))
We need to calculate the number of ways to link them into circle.(we can link 0->1 1->0)
Ways to form n circles with m 01-chains (let's define it as fm, n) equals to Stirling numbers of the first kind. So we consider forming 01-chains with 00 + (10)* + 11 first, then consider forming circles with 01-chains.
Circles which consists with 10 chains only is not able to divide into 01-chains, so let's call them 10-circle and calculate them separately.
Suppose there are (cnt[10] - k) 10-chains which form t 10-circles. Then l = cnt[00] = cnt[11] 01-chains will be formed with k 10-chains. Define gk = l! * k! * C(k + l - 1, l - 1), which equals to the ways to form them.
Define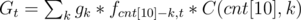
Time Complexity : O(n2)
Here's my code: 20756117
Orz syc1999 who got AC with O(n2) solution just after the contest ended.//It seems his solution based on DP is different from mine...
ANYONE PASSED DIV 2 D IN JAVA WITH 3 DIJIKSTRAS AND PRIORITYQUEUE ?? Getting TLE on case 129 http://codeforces.net/contest/716/submission/20757614
For Div2D, I have a solution similar to the editorial. It was timing out in the contest, but I just realized that was only in the test cases when s and t were not connected. Taking care of this case resulted in AC. My accepted solution.
I am not clear on the complexity of the solution (I think it's O(m*m*logn)). I thought someone might be able to help. My solution is as follows: Initialize all variable edges with weight 1.
In a loop
Find any shortest path. If its length is equal to L we are done. If its length is > L we are done , and the answer is NO.
Otherwise, the length is < L. While calculating the shortest path, we also keep track of the first variable edge in it(starting from s). If there is no such edge, then it means there is a path of length < L, with no variable edge in it. Hence the answer is NO.
Otherwise, increase the length of the variable edge so that the length of the path is L.
My intuition about the time complexity is similar to the editorial. It would be great if someone can help me on this :D.
My idea is similar, I just take the last variable edge in the shortest path found, WA16, here is my solution:
https://codeforces.net/problemset/submission/715/55517344
In div 2 D complete the graph code why the last 2 loops in dij2() are required ?? where the edges are set to -2 and then to infinity
There is another constructive solution for Div1B which has better complexity than the problem setter's solution.
Here is an O(n^2) solution which can be converted to O(m log n) using dijkstra-with-heaps/red-black-trees. The idea is to first do a dijkstra from t and then do a dijkstra from s, assigning weights on the fly. Assign weight (dist(s,t)-dist(nb,t))-dist(s,vt) to edge vt<->nb if this quantity is positive otherwise assign weight 1.
Link to O(n^2) implementation from virtual participation: 28398556
nicely explained DIV2 : D thanks!
Div 2.E Digit Tree can be solved without exclusive but with proper scheduling, just update answer assuming u both as the beginning and the end when you encounter it, using MapDown&MapUp, which record previous nodes . The only thing to keep in mind is to Update MapDown&MapUp only after coming back from a son of a centroid ,to guarantee nodes in the same son not combine with each other.
Can anyone who reads this comment please point out the mistake in my Code for Complete the Graph? I am calculating minimum distance of every vertex from t first. Then I calculate distance from s and update the edge weights to get L as shortest path. What am I missing? Please help