Аркадий прошел n-й уровень в игре Township, и поэтому Маша решила испечь ему торт! Конечно, торт представляет из себя выпуклый n-угольник, то есть многоугольник с n сторонами.
Будучи истинным джентльменом, Аркадий решил поделить торт на две равные по площади части одним прямым разрезом: одну часть он съест сам, другую съест Маша. Но вот незадача: Аркадий уже воткнул нож в одну из точек внутри торта, и теперь ему нужно разрезать торт по прямой линии, проходящей через эту точку.
Помогите Аркадию: найдите такую прямую, что она проходит через точку, в которую Аркадий воткнул нож, и делит торт на две равные по площади части, или определите, что такой прямой нет. Ваша программа должна быстро отвечать на много запросов с одним и тем же тортом, но разными точками, в которые Аркадий втыкает нож.
В первой строке находятся два целых числа n и q (3 ≤ n ≤ 104, 1 ≤ q ≤ 105) — число вершин в торте-многоугольнике и число запросов.
Далее следуют n строк, в которых находятся координаты вершин многоугольников в порядке обхода по часовой стрелке. В i-й из этих строк находятся два целых числа xi и yi ( - 106 ≤ xi, yi ≤ 106) — координаты i-й вершины. Гарантируется, что многоугольник строго выпуклый, в частности, никакие три вершины не лежат на одной прямой.
Далее следует пустая строка.
Далее следуют q строк, в которых находятся координаты точек, в которые Аркадий втыкает нож. В i-й из этих строк находятся два целых числа xi и yi ( - 106 ≤ xi, yi ≤ 106) — координаты точки, в которую Аркадий втыкает нож, в i-м запросе. Гарантируется, что в каждом запросе точка лежит строго внутри многоугольника, в частности, не лежит на его границе.
Для каждого запроса выведите одно число — полярный угол прямой, являющейся ответом на соответствующий запрос. Угол должен принадлежать отрезку [0;π], углы отсчитываются от направления оси абцисс (OX) против часовой стрелки. Например, полярный угол направления оси ординат (OY) равен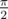 
. Если в запросе не существует подходящей прямой, выведите -1.
Если подходящий прямых несколько, выведите любую из них. Ваш ответ будет считаться правильным, если отношение модуля разности площадей получившихся частей к общей площади многоугольника, не превосходит 10 - 4. Иными словами, если a и b — площади получившихся частей многоугольника, то ваш ответ будет считаться правильным, если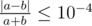 
.
3 1
0 0
0 3
3 0
1 1
2.67794504460098710000
5 3
6 5
6 3
5 0
0 0
0 5
5 4
3 3
5 2
0.60228734612690049000
1.27933953226473580000
2.85805511179015910000
