| Codeforces Round 411 (Div. 1) |
|---|
| Закончено |
В Исарте люди живут вечно. Среди них есть n банд злоумышленников. В i-й банде состоят si человек, пронумерованных от 0 до si - 1. Некоторые из них однажды приняли участие в большом ограблении шахты и украли каждый по одному золотому слитку (эти люди заданы во входных данных). Это произошло 10100 лет назад и с тех пор все банды уехали далеко от городов.
Все эти годы бандиты копировали некоторые золотые слитки в соответствии с определенным планом, чтобы не быть пойманными. Они построили ориентированный граф-турнир (то есть граф, в котором между каждой парой вершин есть одно направленное ребро), вершины в котором — банды (граф задан во входных данных). В этом графе ребро из вершины u в вершину v означало, что в i-й час человек номер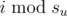 
из банды u может послать фальшивый слиток человеку номер 
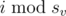из банды v. Он посылает слиток, только если у него есть какой-то слиток (настоящий или фальшивый), а у получателя нет слитков. Таким образом, в каждый момент времени каждый бандит имел один или ноль слитков. Некоторые из бандитов имели настоящие слитки, некоторые — фальшивые.
В начале этого года полиции удалось найти банды, но, как всегда, поймать их она пока не может. Полиция решила открыть ювелирный магазин, чтобы бандиты попытались продать слитки. Теперь каждый бандит, у которого есть слиток (подлинный или фальшивый), попробует его продать. Если слиток подлинный, то он его без проблем продаст, а если фальшивый, то может случиться одна из двух ситуаций:
- Бандит успешно продаст слиток.
- Бандит будет арестован полицией.
Сила банды равна числу бандитов, которые успешно продали свой слиток. После того, как все продажи завершены, полиция арестует b банд из самых сильных. Банда с силой p состоит в самых сильных бандах, если и только если не более чем a - 1 банда имеет силу строго больше p. Рассмотрим всевозможные результаты продажи фальшивых слитков и всевозможные способы выбрать b банд из самых сильных банд. Подсчитайте, сколько различных множеств могут образовать эти b банд по модулю 109 + 7. Два множества X и Y считаются различными, если некоторая банда есть в X, но ее нет в Y.
Первая строка содержит три целых числа n, a и b (1 ≤ b ≤ a ≤ n ≤ 5·103) — количество банд и числа a и b из условия.
Далее следуют n строк, каждая из них содержит строку длины n из нулей и единиц. Если j-й символ i-й строки равен 1, то из вершины i в вершину j есть ребро. Гарантируется, что aii = 0, и aij + aji = 1 при i ≠ j.
Далее следуют n строк, каждая начинается с числа si (1 ≤ si ≤ 2·106) — количеству бандитов в i-й банде, и затем содержит строку из нулей и единиц длины si. j-й символ равен 0, если j-й человек i-й банды имел настоящий слиток изначально, иначе символ равен 1. Гарантируется, что сумма si не превосходит 2·106.
Выведите одно число: количество различных множеств из b банд, которые полиция может арестовать по модулю 109 + 7.
2 2 1
01
00
5 11000
6 100000
2
5 2 1
00000
10000
11011
11000
11010
2 00
1 1
6 100110
1 0
1 0
5
