| Codeforces Round 431 (Div. 1) |
|---|
| Закончено |
От начала времён до конца света, послание ждало своего носителя.
Пусть задан неупорядоченный набор из n строчных латинских букв, каждая буква может встречаться несколько раз. Будем считать, что все буквы — это строки длины 1, и повторим следующую операции n - 1 раз:
- Уберем две строки s и t из набора и добавим их конкатенацию s + t в набор.
Стоимость такой операции равна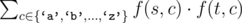 
, где f(s, c) означает число вхождений символа c в строку s.
По данному неотрицательному числу k постройте любой корректный непустой набор из не более чем 100 000 букв такой, что минимальная суммарная стоимость процесса для него равна в точности k. Можно показать, что такой набор всегда существует.
Единственная строка содержит одно целое число k (0 ≤ k ≤ 100 000) — необходимая минимальная стоимость.
Выведите непустую строку из не более чем 100 000 строчных латинских букв — любой набор, удовлетворяющий ограничениям, без пробелов.
12
abababab
3
codeforces
Для набора {'a', 'b', 'a', 'b', 'a', 'b', 'a', 'b'} один из способов выполнить процесс это следующий:
- {"ab", "a", "b", "a", "b", "a", "b"}, стоимость операции 0;
- {"aba", "b", "a", "b", "a", "b"}, стоимость операции 1;
- {"abab", "a", "b", "a", "b"}, стоимость операции 1;
- {"abab", "ab", "a", "b"}, стоимость операции 0;
- {"abab", "aba", "b"}, стоимость операции 1;
- {"abab", "abab"}, стоимость операции 1;
- {"abababab"}, стоимость операции 8.
Суммарная стоимость равна 12, можно доказать, что это минимальная стоимость.
Обратите внимание, что выведенная строка не обязательно быть равна финальной строке, достаточно лишь, чтобы она отвечала подходящему набору букв.
