| Codeforces Round 431 (Div. 1) |
|---|
| Закончено |
Куда бы мы не шли, кого бы не нашли, на нашем месте, исполним эту песню вместе!
На плоскости расположена прямоугольная сцена размера w × h с вершинами в точках (0, 0), (w, 0), (w, h) и (0, h).
По краям сцены находятся n танцоров. i-й из них относится к одной из следующих групп:
- Вертикальные: стоит в (xi, 0), двигается в положительном направлении y (вверх);
- Горизонтальные: стоит в (0, yi), двигается в положительном направлении x (вправо).
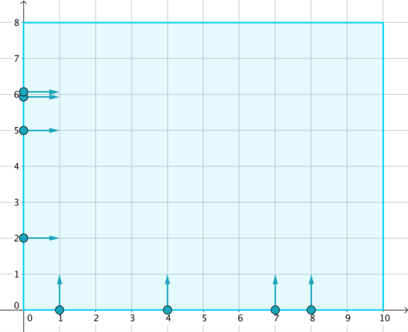
В соответствии с планом танца, i-й танцор должен стоять на месте первые ti миллисекунд, а затем начать двигаться в заданном направлении со скоростью 1 единица в миллисекунду, пока не достигнет другого края сцены. Никакие два танцора не имеют одновременно совпадающую группу, позицию и время ожидания.
Когда два танцора сталкиваются (т.е. находятся в одной точке, и оба из них двигаются), они мгновенно обмениваются направлениями движения и продолжают двигаться.
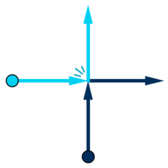
Танцоры останавливаются, как только они достигнут границы. Найдите точку остановки для каждого танцора.
Первая строка содержит три целых числа n, w и h (1 ≤ n ≤ 100 000, 2 ≤ w, h ≤ 100 000) — число танцоров, ширина и высота сцены, соответственно.
Каждая из следующих n строк описывает танцора: i-я из них содержит три целых числа gi, pi и ti (1 ≤ gi ≤ 2, 1 ≤ pi ≤ 99 999, 0 ≤ ti ≤ 100 000), описывающие группу танцора gi (gi = 1 — вертикальные, gi = 2 — горизонтальные), позицию, и время ожидания. Если gi = 1, то pi = xi; иначе pi = yi. Гарантируется, что 1 ≤ xi ≤ w - 1 и 1 ≤ yi ≤ h - 1. Гарантируется, что никакие два танцора не имеют одинаковую группу, позицию и время одновременно.
Выведите n строк, i-я из которых содержит два целых числа (xi, yi) — позицию остановки i-го танцора.
8 10 8
1 1 10
1 4 13
1 7 1
1 8 2
2 2 0
2 5 14
2 6 0
2 6 1
4 8
10 5
8 8
10 6
10 2
1 8
7 8
10 6
3 2 3
1 1 2
2 1 1
1 1 5
1 3
2 1
1 3
Первый пример соответствует начальной расстановке, показанной в условии, траектории танцоров показаны различными цветами на следующем рисунке.
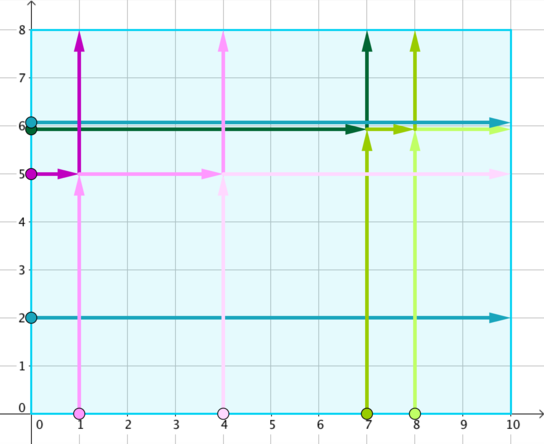
Во втором примере никакие танцоры не сталкиваются.
| Название |
|---|




