Дано множество, состоящее из n точек в пятимерном пространстве. Точки пронумерованы от 1 до n. Никакие две точки не совпадают.
Назовем точку a плохой, если существуют две разные точки b и c из данного множества, не совпадающие с a, такие что угол между векторами 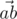 и
и 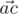 острый (строго меньше
острый (строго меньше 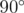 ). Иначе, назовем точку хорошей.
). Иначе, назовем точку хорошей.
Угол между векторами 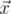 и
и 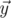 в пятимерном пространстве определен как
в пятимерном пространстве определен как 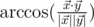 , где
, где 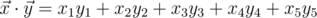 — скалярное произведение и
— скалярное произведение и 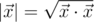 — длина вектора
— длина вектора 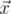 .
.
Выведите индексы всех хороших точек в порядке возрастания.
Первая строка входных данных содержит одно целое число n (1 ≤ n ≤ 103) — количество точек.
Следующие n строк содержат по пять целых чисел ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103) — координаты i-й точки. Все точки различны.
Выведите число k — количество хороших точек.
В следующих k строках выведите индексы хороших точек в возрастающем порядке.
6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1
1
3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0
0
В первом примере, первая точка образует угол ровно 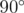 со всеми другими парами точек, поэтому она является хорошей.
со всеми другими парами точек, поэтому она является хорошей.
Во втором примере точки лежат в плоскости cd и выглядят так:
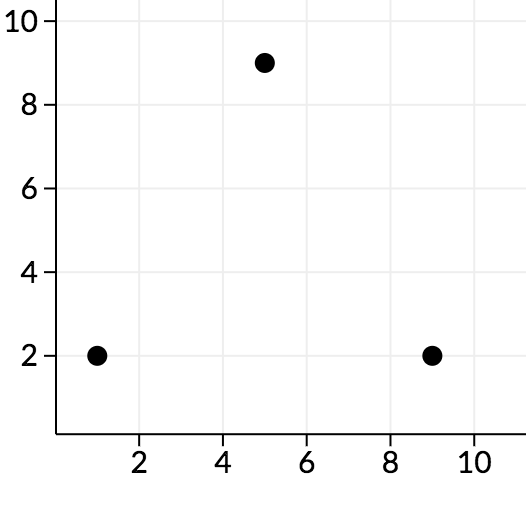
Видно, что все углы острые, поэтому ни одна точка не является хорошей.
| Название |
|---|




