В Берляндии приближаются президентские выборы! Каждый с нетерпением ожидает этого события!
В Берляндии есть n жителей и три кандидата — Алексей, Борис и Владимир. Так как выборы определят будущее страны на много лет, каждый из n жителей выберет один из шести возможных порядков на кандидатах случайно, равновероятно и независимо от остальных жителей.
Для увеличения прозрачности процесса выборов правительство разработало функцию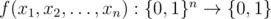 
(т.е. функция принимает n булевых аргументов и возвращает булевый результат). Функция удовлетворяет следующему условию: f(1 - x1, 1 - x2, ..., 1 - xn) = 1 - f(x1, x2, ..., xn).
Будет проведено три раунда выборов между каждой парой кандидатов: Алексеем и Борисом, Борисом и Владимиром, Владимиром и Алексеем. В каждом раунде xi будет равно 1, если i-й житель предпочитает первого кандидата второму (т.е. в его списке предпочтений первый кандидат находится раньше второго), и 0 иначе. После этого определяется величина y = f(x1, x2, ..., xn). Если y = 1, то первый кандидат считается победителем этого раунда, иначе, если y = 0, второй считается победителем раунда.
Определим вероятность того, что есть кандидат, победивший в двух раундах, p. p·6n всегда целое число. Выведите это число по модулю 109 + 7 = 1 000 000 007.
Первая строка содержит число n (1 ≤ n ≤ 20).
Следующая строка содержит строку длины 2n из нулей и единиц, представляющую функцию f. Определим bk(x) как k-й бит x. Тогда i-й символ строки есть f(b1(i), b2(i), ..., bn(i)) (символы строки нумеруются с нуля).
Гарантируется, что f(1 - x1, 1 - x2, ..., 1 - xn) = 1 - f(x1, x2, ..., xn) для всех значений x1, x2, ldots, xn.
Одно число — ответ на задачу.
3
01010101
216
3
01101001
168
В первом примере f(x1, x2, x3) = x1, т.е. результат полностью определятся первым жителем. Тогда первый кандидат в порядке предпочтений первого жителя победит в двух турах. Следовательно, p = 1 и ответ на задачу 1·63 = 216.
