Дана вершина дерева с номером 1 и весом 0. Обозначим за cnt количество вершин в дереве в любой момент (изначально cnt равно 1). Необходио обработать Q запросов, каждый из которых имеет один из двух типов:
-
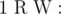 Добавить новую вершину (с номером cnt + 1) и весом W и провести ребро между вершиной R и этой вершиной.
Добавить новую вершину (с номером cnt + 1) и весом W и провести ребро между вершиной R и этой вершиной. -
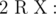 Выведите максимальную длину последовательности вершин такой, что она
Выведите максимальную длину последовательности вершин такой, что она - Начинается с вершины R.
- Каждая следующая вершина является предком предыдущей вершины
- Сумма весов вершин в последовательности не превосходит X.
- Для любой пары i, j вершин, которые являются соседними в последовательности и вершина i является предком вершины j, выполнено w[i] ≥ w[j], а также не существует вершины k на простом пути из i в j такой, что w[k] ≥ w[j]
Дерево подвешено за вершину 1 в любой момент.
Учтите, что запросы заданы в зашифрованном виде.
В первой строке задано количество запросов Q (1 ≤ Q ≤ 400000).
Обозначим за last ответ на предыдущий запрос типа 2 (изначально last равно 0).
Каждая из следующих Q строк содержит описание запроса в одном из следующих форматов:
- 1 p q (1 ≤ p, q ≤ 1018): Это запрос первого типа, где
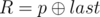 и
и 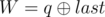 . Гарантируется, что 1 ≤ R ≤ cnt и 0 ≤ W ≤ 109.
. Гарантируется, что 1 ≤ R ≤ cnt и 0 ≤ W ≤ 109. - 2 p q (1 ≤ p, q ≤ 1018): Это запрос второго типа, где
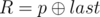 и
и 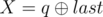 . Гарантируется, что 1 ≤ R ≤ cnt и 0 ≤ X ≤ 1015.
. Гарантируется, что 1 ≤ R ≤ cnt и 0 ≤ X ≤ 1015.
 обозначает побитовый XOR чисел a и b.
обозначает побитовый XOR чисел a и b.
Гарантируется, что есть хотя бы один запрос второго типа.
Для каждого запроса второго типа выведите ответ на него в отдельной строке.
6
1 1 1
2 2 0
2 2 1
1 3 0
2 2 0
2 2 2
0
1
1
2
6
1 1 0
2 2 0
2 0 3
1 0 2
2 1 3
2 1 6
2
2
3
2
7
1 1 2
1 2 3
2 3 3
1 0 0
1 5 1
2 5 0
2 4 0
1
1
2
7
1 1 3
1 2 3
2 3 4
1 2 0
1 5 3
2 5 5
2 7 22
1
2
3
В первом тестовом примере,
last = 0
- Запрос 1: 1 1 1, Вершина 2 с весом 1 подвешивается к вершине 1.
- Запрос 2: 2 2 0, Никакая последовательность вершин, начинающаяся с вершины 2, не имеет сумму весов не более 0. last = 0
- Запрос 3: 2 2 1, Ответ равен 1, так как требуемая последователньость равна {2}. last = 1
- Запрос 4: 1 2 1, Вершина 3 с весом 1 подвешивается к вершине 2.
- Запрос 5: 2 3 1, Ответ равен 1, так как требуемая последовательность равна {3}. Вершина 2 не может быть добавлена к последовательности, так как сумма весов должна быть не более 1. last = 1
- Запрос 6: 2 3 3, Ответ равен 2, так как требуемая последовательность будет равна {3, 2}. last = 2
| Название |
|---|




