Определим m-свободную матрицу, как бинарную (то есть содержащую только символы 1 и 0) матрицу такую, что любая квадратная подматрица m × m этой матрицы содержит хотя бы один ноль.
Рассмотрим следующую задачу:
Даны два целых числа n и m. Постройте m-свободную квадратную матрицу размера n × n такую, что количество символов 1 в ней максимально. Выведите максимальное количество символов 1 в такой матрице.
Эту задачу вам решать совсем не обязательно. Вместо этого вы поможете составить к ней тесты.
Задано t чисел x1, x2, ..., xt. Для каждого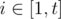 
найдите два целых числа ni и mi (ni ≥ mi) такие, что ответ для вышеприведенной задачи равен в точности xi, если установить n = ni и m = mi.
В первой строке задано одно целое число t (1 ≤ t ≤ 100) — количество тестов, которые вам нужно составить.
Затем следуют t строк, в i-й записано одно целое число xi (0 ≤ xi ≤ 109).
Обратите внимание, во взломах можно использовать только t = 1.
На каждый тест, который вам нужно составить, выведите два целых числа ni и mi (1 ≤ mi ≤ ni ≤ 109) такие, что максимальное количество символов 1 в mi-свободной матрице размера ni × ni в точности равно xi. Если решений несколько, выведите любое; если невозможно построить такой тест, то выведите единственной число - 1.
3
21
0
1
5 2
1 1
-1
