Дано дерево (граф состоящий из n вершин, соединенных n - 1 ребрами, в котором от каждой вершины можно добраться до каждой, двигаясь только по ребрам).
Вершину можно уничтожить если из нее выходит четное число ребер, при этом уничтожаются все ребра, выходящие из нее.
Требуется уничтожить все вершины в дереве, либо сказать, что это невозможно.
В первой строке задано целое число n (1 ≤ n ≤ 2·105) — количество вершин в дереве.
Во второй строке заданы n целых чисел p1, p2, ..., pn (0 ≤ pi ≤ n). Если pi ≠ 0, то существует ребро между вершинами с номерами i и pi. Гарантируется, что задано дерево.
Если уничтожить все вершины возможно, выведите «YES» (без кавычек), иначе выведите «NO» (без кавычек).
Если возможно уничтожить все вершины, в следующих n строках выведите номера вершин в порядке, в котором их надо уничтожать. Если существует несколько способов удалить все вершины, выведите любой.
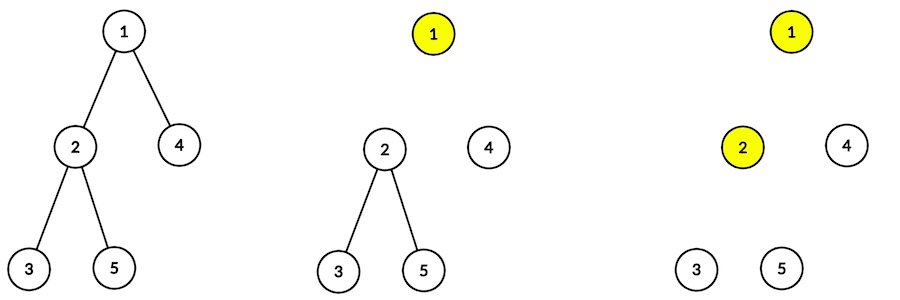
5
0 1 2 1 2
YES
1
2
3
5
4
4
0 1 2 3
NO
В первом примере сначала нужно уничтожить вершину с номером 1 (при ее уничтожении удалятся ребра (1, 2) и (1, 4)), затем 2-ю (удаляются ребра (2, 3) и (2, 5)). После этого в дереве не остается ребер, поэтому оставшиеся вершины можно уничтожать в любом порядке.
| Название |
|---|




