Hello everyone! There is a problem in an Olympiad from my country 5 years ago, but I could not solve it, nor some of my friends. So I wanted to ask for help with this problem. The problem is as follows:

Given a bipartite graph with $$$n$$$ nodes on the left side and $$$m$$$ nodes on the right side. There is also a weight matrix $$$C$$$, $$$C_{i,j}$$$ is the weight of the edge connecting the $$$i$$$-th node on the left side to the $$$j$$$-th node on the right side. The problem ask to find a sub-tree of the graph with minimum total edge weight and it connects every nodes on the left side. In other word, we need to find a minimum Steiner tree, whose terminals are nodes on the left side. It is guaranteed that the answer exists.

Constraints: $$$n, m \le 1000$$$. $$$-1 \le C_{i, j} \le 10000$$$. $$$C_{i, j} = -1$$$ means there is no edge connecting the $$$i$$$-th node on the left side and $$$j$$$-th node on the right side (or it can be considered $$$+\infty$$$).

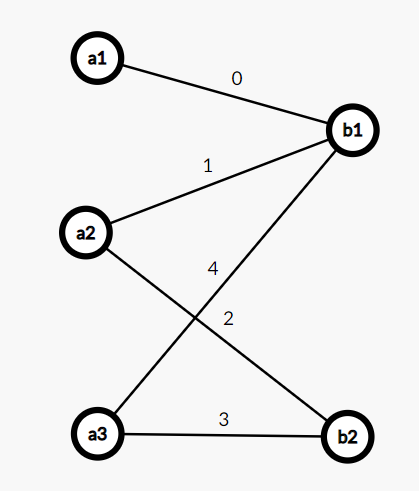
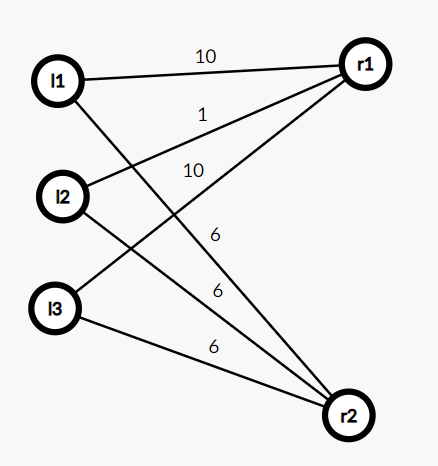
Here is the samples from the problem statement.

4 3
 0 -1  5
 0  4  4
-1  0 -1
 1  2  0

4 4
 0 -1  5  3
-1  4  5 -1
-1  0 -1  0
 6  6  0 -1

Also some interseting examples that my friend has drawn:

I have done some Googling, but it's no good. I have found a Wikipedia article called Quasi bipartitie graph and there were only approximating solutions. But I'm not sure if this article has anything to do with this problem.

Please help me find a solution to this problem, or maybe help me prove this is an NP problem, because I'm really depressed :(.