# The handless (blindfolded ?) barman and his prankster intern↵
↵
↵
## The problem↵
↵
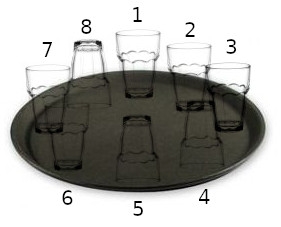
A handless barman has $n = 2^k$ glass placed in circle on a tray.↵
Some of them are upside-down, some of them are right side up.↵
He want every glass to be right side up, but he is handless.↵
He needs the help of his intern. The barman can ask the intern to flip the glass in some set of positions. But the intern is a prankster ! He will rotate the tray (circularly shifting the positions of the glass) before performing the flips. The intern stops the game when every glass is right side up.↵
Find a strategy for the barman to achieve this.↵
↵
↵
↵
This problem can be instantiated in many ways, depending on the information the barman has (if he sees the glass / if he is totally blindfolded / if he knows the number of glass in right side up position).↵
↵
You can see how it is linked with [problem C of GCJ 2022 1B](https://codingcompetitions.withgoogle.com/codejam/round/000000000087711b/0000000000acd29b).↵
↵
I want to add my polynomial point of view of this type of problem.↵
↵
## Solution when the barman isn't blindfolded↵
The barman sees the glass, how to solve the problem in $n$ rounds ?↵
↵
<spoiler summary="Solution">↵
The barman use this simple strategy : he asks the intern to flip the set of positions where the glass are upside-down, until every glass is right side up.↵
We'll show that this strategy ends after at most $n$ rounds.↵
↵
Let $A := F_2[X] / (X^n + 1)$.↵
↵
We can model the state of the tray by a polynomial ↵
$$ a_1 + a_2 X + \dots + a_{n}X^{n - 1} \in A$$↵
where $a_i = 1$ if the glass in position $i$ is upside-down and $0$ otherwise.↵
A cyclic shift is the multiplication by a power of $X$, and a set of flips is the addition of a polynomial $Q$.↵
↵
Let $P_0 \in A$ be the starting configuration.↵
We see that, when performing our simple strategy on round $i$, the configuration $P_i$ becomes $P_{i + 1} := (1 + X^{d_i})P_i$, where $d_i$ is the rotation chosen by the intern.↵
↵
Thus, after $n$ rounds, the configuration is :↵
$$P_n = (X^{d_n} + 1) \dots (X^{d_2} + 1) (X^{d_1} + 1)P_0$$↵
where $d_1, \dots d_n$ are the cyclic shifts indices. We have :↵
$$X^n + 1 = (X + 1)^n$$ ↵
because $n = 2^k$ and↵
$$X^{d_i} + 1 = (X + 1)(X^{d_i - 1} + \dots + X + 1)$$↵
↵
Thus $X^n + 1 = (X + 1)^n$ divides $P_n$ : we have $P_n = 0$, and every glass is right-side up.↵
</spoiler>↵
↵
## Solution when the barman is blindfolded↵
The barman is blindfolded, how to solve the problem in $2^n - 1$ rounds ?↵
↵
<spoiler summary="Solution Overview">↵
The barman's strategy is `Solve(0)`, where :↵
↵
~~~~~↵
Solve(i) {↵
if(i == n) return;↵
Solve(i + 1)↵
play (1 + X)^i↵
Solve(i + 1);↵
}↵
~~~~~↵
↵
We consider the injective function $f$ :↵
$$P \in A \mapsto (P, P (1 + X), P (1 + X)^2, \dots, P (1 + X)^{n - 1}) \in A^n$$↵
We remark that if we play $(1 + X)^i$ on configuration $P$, the polynomials $f(P)_{n - i}, \dots f(P)_{n - 1}$ do not change since, if $i + j \geq n$ :↵
$$f(P + X^d (1 + X)^i)_j = (P + X^d (1 + X)^i) (1 + X)^j = P (1 + X)^j + X^d (1 + X)^{i + j} = f(P)_j$$↵
Of course, $f(P)_{n - i}$ do change.↵
↵
Thus, playing the $(1 + X)^i$ in a Grey-code way gives $2^n$ different images of $P$ through $f$, thus we explore each one of the $2^n$ configurations of $P$.↵
↵
The $(1 + X)^i$ are in fact the rows of the Sierpinski triangle (Pascal triangle mod $2$).↵
</spoiler>↵
↵
I hope it's understandable.↵
Of course, when we know more information, we can speed up this search by skipping sub-trees.↵
↵
## Generalizations↵
↵
We can easily prove that when $n$ is not a power of $2$, the barman can't win.↵
We can try to solve the problem with a group $G$ different than $\mathbb{Z} / n \mathbb{Z}$ (circular rotations) for the transformations performed by the intern : we want to study the nilpotent elements of the group algebra $F_2[G]$.↵
For example, we can solve the problem on a giant tray, on which we have placed small trays in circle, on which we have placed the glass.↵
↵
## Fun story↵
Exactly three days before round 1B, I explained this polynomial approach to the Network and Optimization team in CWI. It's one of my favorite problems since it relates a combinatorics game with algebra and number theory.↵
In fact, I have only presented the unblindfolded case to the N&O team, and only mentioned the blindfolded case. A member of the team did the GCJ 1B and was really frustrated of this :p↵
He only told it to me today, it's why I come after the storm.
↵
↵
## The problem↵
↵
A handless barman has $n = 2^k$ glass placed in circle on a tray.↵
Some of them are upside-down, some of them are right side up.↵
He want every glass to be right side up, but he is handless.↵
He needs the help of his intern. The barman can ask the intern to flip the glass in some set of positions. But the intern is a prankster ! He will rotate the tray (circularly shifting the positions of the glass) before performing the flips. The intern stops the game when every glass is right side up.↵
Find a strategy for the barman to achieve this.↵
↵
↵
↵
This problem can be instantiated in many ways, depending on the information the barman has (if he sees the glass / if he is totally blindfolded / if he knows the number of glass in right side up position).↵
↵
You can see how it is linked with [problem C of GCJ 2022 1B](https://codingcompetitions.withgoogle.com/codejam/round/000000000087711b/0000000000acd29b).↵
↵
I want to add my polynomial point of view of this type of problem.↵
↵
## Solution when the barman isn't blindfolded↵
The barman sees the glass, how to solve the problem in $n$ rounds ?↵
↵
<spoiler summary="Solution">↵
The barman use this simple strategy : he asks the intern to flip the set of positions where the glass are upside-down, until every glass is right side up.↵
We'll show that this strategy ends after at most $n$ rounds.↵
↵
Let $A := F_2[X] / (X^n + 1)$.↵
↵
We can model the state of the tray by a polynomial ↵
$$ a_1 + a_2 X + \dots + a_{n}X^{n - 1} \in A$$↵
where $a_i = 1$ if the glass in position $i$ is upside-down and $0$ otherwise.↵
A cyclic shift is the multiplication by a power of $X$, and a set of flips is the addition of a polynomial $Q$.↵
↵
Let $P_0 \in A$ be the starting configuration.↵
We see that, when performing our simple strategy on round $i$, the configuration $P_i$ becomes $P_{i + 1} := (1 + X^{d_i})P_i$, where $d_i$ is the rotation chosen by the intern.↵
↵
Thus, after $n$ rounds, the configuration is :↵
$$P_n = (X^{d_n} + 1) \dots (X^{d_2} + 1) (X^{d_1} + 1)P_0$$↵
where $d_1, \dots d_n$ are the cyclic shifts indices. We have :↵
$$X^n + 1 = (X + 1)^n$$ ↵
because $n = 2^k$ and↵
$$X^{d_i} + 1 = (X + 1)(X^{d_i - 1} + \dots + X + 1)$$↵
↵
Thus $X^n + 1 = (X + 1)^n$ divides $P_n$ : we have $P_n = 0$, and every glass is right-side up.↵
</spoiler>↵
↵
## Solution when the barman is blindfolded↵
The barman is blindfolded, how to solve the problem in $2^n - 1$ rounds ?↵
↵
<spoiler summary="Solution Overview">↵
The barman's strategy is `Solve(0)`, where :↵
↵
~~~~~↵
Solve(i) {↵
if(i == n) return;↵
Solve(i + 1)↵
play (1 + X)^i↵
Solve(i + 1);↵
}↵
~~~~~↵
↵
We consider the injective function $f$ :↵
$$P \in A \mapsto (P, P (1 + X), P (1 + X)^2, \dots, P (1 + X)^{n - 1}) \in A^n$$↵
We remark that if we play $(1 + X)^i$ on configuration $P$, the polynomials $f(P)_{n - i}, \dots f(P)_{n - 1}$ do not change since, if $i + j \geq n$ :↵
$$f(P + X^d (1 + X)^i)_j = (P + X^d (1 + X)^i) (1 + X)^j = P (1 + X)^j + X^d (1 + X)^{i + j} = f(P)_j$$↵
Of course, $f(P)_{n - i}$ do change.↵
↵
Thus, playing the $(1 + X)^i$ in a Grey-code way gives $2^n$ different images of $P$ through $f$, thus we explore each one of the $2^n$ configurations of $P$.↵
↵
The $(1 + X)^i$ are in fact the rows of the Sierpinski triangle (Pascal triangle mod $2$).↵
</spoiler>↵
↵
I hope it's understandable.↵
Of course, when we know more information, we can speed up this search by skipping sub-trees.↵
↵
## Generalizations↵
↵
We can easily prove that when $n$ is not a power of $2$, the barman can't win.↵
We can try to solve the problem with a group $G$ different than $\mathbb{Z} / n \mathbb{Z}$ (circular rotations) for the transformations performed by the intern : we want to study the nilpotent elements of the group algebra $F_2[G]$.↵
For example, we can solve the problem on a giant tray, on which we have placed small trays in circle, on which we have placed the glass.↵
↵
## Fun story↵
Exactly three days before round 1B, I explained this polynomial approach to the Network and Optimization team in CWI. It's one of my favorite problems since it relates a combinatorics game with algebra and number theory.↵
In fact, I have only presented the unblindfolded case to the N&O team, and only mentioned the blindfolded case. A member of the team did the GCJ 1B and was really frustrated of this :p↵
He only told it to me today, it's why I come after the storm.





