Problem: Rectangle Shrinking

Part 1: Notations

$$$x$$$: A brick. $$$x_i$$$ denotes the part of $$$x$$$ belonging to the $$$i$$$-th floor. For example, if $$$x.u=1,\,x.d=2$$$, then $$$x_1.u=x_1.d=1$$$, $$$x_2.u=x_2.d=2$$$, and $$$x_1.l=x_2.l=x.l$$$, $$$x_1.r=x_2.r=x.r$$$.

$$$A_i,\,i=1,2$$$: The set of bricks whose $$$u=d=i$$$.

$$$B$$$: The set of bricks whose $$$u=1,\,d=2$$$.

$$$\texttt{Remove}$$$: Remove a brick $$$x$$$.

$$$\texttt{Shrink}$$$: Shrink a brick $$$x$$$ to another non-empty brick.

$$$\texttt{Keep}$$$: Keep a brick $$$x$$$ unchanged.

Note that in our solution we may operate on a part of brick. For example, for a brick $$$x \in B$$$, we may $$$\texttt{Keep}\,x_1$$$ while $$$\texttt{Remove}\,x_2$$$.

Part 2: Idea

I think $$$\texttt{Shrink}$$$ing $$$x \in B$$$ is troublesome. If you shrink $$$x_1$$$, you have to shrink $$$x_2$$$ in the same way, i.e., $$$x_1$$$ has to be aligned with $$$x_2$$$. So is there a solution that only performs $$$\texttt{Remove}$$$ and $$$\texttt{Keep}$$$ on every $$$x \in B$$$? But that is impossible, because the bricks $$$x, y \in B$$$ may overlap themselves even with considering $$$A$$$. So what if $$$B$$$ are pairwise non-overlapping (because we could perform some pre-$$$\texttt{Shrink}$$$ and pre-$$$\texttt{Remove}$$$ to make $$$B$$$ pairwise non-overlapping)?

In that case, we can consider each floor independently. Let

$$$C_i := A_i \cup \{x_i \mid x \in B \}$$$.

For example, if

$$$A_1 = \{[u=1, d=1, l=2, r=5], [u=1, d=1, l=7, r=10]\}$$$,

$$$B=\{[u=1, d=2, l=2, r=2], [u=1, d=2, l=4, r=7]\}$$$, then

$$$C_1 = \{[u=1, d=1, l=2, r=2], [u=1, d=1, l=2, r=5], [u=1, d=1, l=4, r=7], [u=1, d=1, l=7, r=10]\}$$$.

We sort $$$C_i$$$ w.r.t $$$l$$$, and traverse $$$C_i$$$ like $$$\texttt{for(auto x: C_i)}$$$.

Case 1 ($$$\texttt{Keep}$$$): If $$$x$$$ is not overlapping now, then we add $$$x$$$ to the answer, no matter if $$$x$$$ is from $$$A_i$$$ or not.

Case 2 ($$$\texttt{Remove}$$$): If $$$x$$$ is fully contained in the union of other rectangles, then we always remove $$$x$$$, no matter if $$$x$$$ is from $$$A_i$$$ or not.

$$$\texttt{Keep}$$$ and $$$\texttt{Remove}$$$ are relatively easier, no matter $$$x \in A_i$$$ or $$$x \in \{x_i \mid x \in B \}$$$.

Case 3 ($$$\texttt{Shrink}$$$): If $$$x$$$ is partially overlapping with other bricks.

Case 3.1: If $$$x \in A_i$$$: $$$\texttt{Shrink} x$$$. Move the $$$x.l$$$ to the right to avoid overlapping.

Case 3.2: If $$$x \in \{x_i \mid x \in B \}$$$: $$$\texttt{Shrink}$$$ all bricks that overlap with $$$x$$$ by moving their right endpoints (i.e., *.r), to the left.

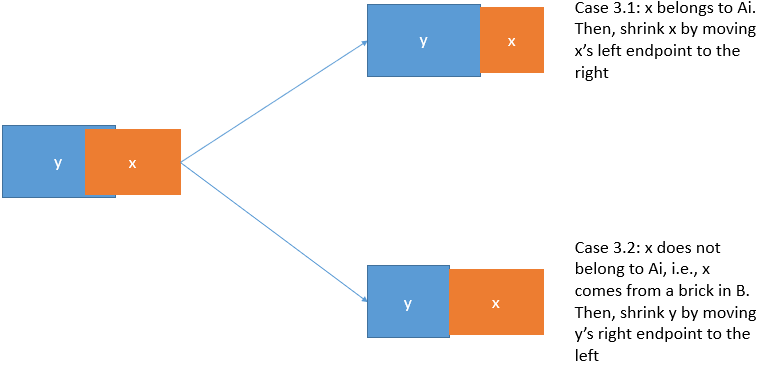
It is guaranteed in Case 3.2 that every brick overlapping with $$$x$$$ is from $$$A_i$$$ because we have already performed pre-calculations in $$$B$$$ to make them non-overlapping. The complexity is not an issue, by amortized analysis, each $$$x \in A_i$$$ will do $$$\texttt{Remove}$$$ at most once and $$$\texttt{Remove}+\texttt{Shrink}$$$ at most twice (keep/move left endpoint+keep/move right endpoint).

Part 3: Implementation

First I copy a range-set implementation from nok0. Basically, it maintains a set of intervals using $$$\texttt{std::set}$$$. When inserting/erasing a range, it can merge/split intervals automatically, using binary search (Yes, stop learning useless algorithms, go to learn binary search!). It supports many APIs, here are some useful APIs in our implementation:

(1) $$$\texttt{Insert(l, r)}$$$: Insert an interval $$$[l, r]$$$.

(2) $$$\texttt{covered_by(l, r)}$$$: Return an interval covering $$$[l, r]$$$, if not exists, returning $$$(-\inf, \inf)$$$.

(3) $$$\texttt{covered(l, r)}$$$: Return a bool variable indication whether interval $$$[l, r]$$$ is fully covered.

(4) $$$\texttt{right(x)}$$$ (added by me): Return $$$\min \{y|y > x, y \text{ is not covered}\}$$$