Hello Codeforces!

Data Structure is a legendary subject that it's really hard for me write it down completely in a single blog, so let's discuss simple DSU first.

DSU is really easy for beginners to understand. Also, this blog talks about more than the simplest DSU.

UPD 2023-1-19: Time complexity analysis updated, thanks Everule for help.

Part 0 — How does DSU works?

Firstly, DSU is short for "Disjoint Set Union". Let's go to a simple task then.

There are $$$n$$$ elements, the $$$i$$$-th element is in the $$$i$$$-th set initially, and now you can do $$$m$$$ queries below: — M a b, to merge the set that $$$a$$$ belongs to and the set that $$$b$$$ belongs to into a new set. If $$$a$$$ and $$$b$$$'ve been in a set already, then do nothing. — Q a b, to tell if $$$a$$$ and $$$b$$$ are in the same set.

Let's go straight to the problem solution.

Solution：

Let's consider contructing a graph. Initially we have self-cycles for all vertecies, which means there are edges $$$i\to i$$$, and $$$\text{root} (i)=i$$$.

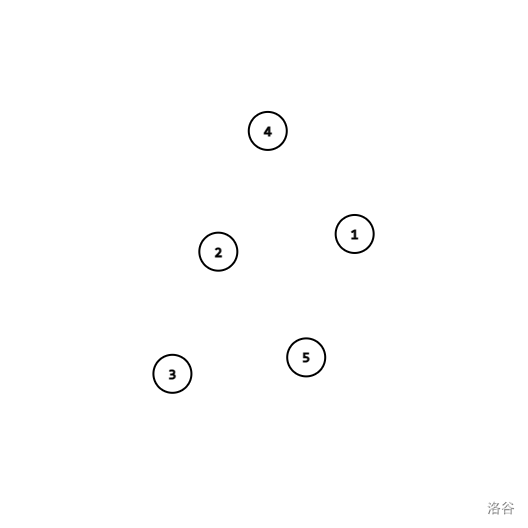
The graph above is the initial state of the graph.

Then if you do M a b operation, then we can match $$$\text{root} (a)$$$ with $$$\text{root} (b)$$$. Which means we can making a new edge $$$\text{root}(a)\to \text{root}(b)$$$.

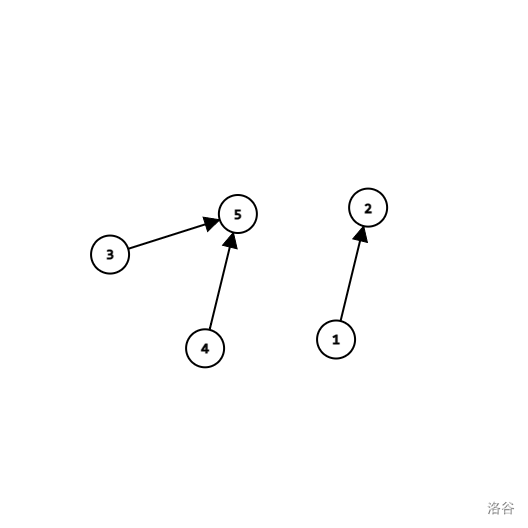
The graph above is the state of the graph at some point, if we do M 1 3, then since the root of $$$1$$$ is $$$2$$$, the root of $$$3$$$ is $$$5$$$, so:

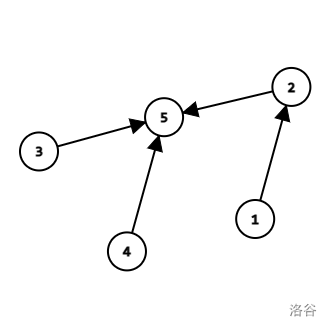
The graph above is the state after M 1 3.

Note that the direction of the edges is not important.

Now we can write out a code to implement the algorithm above.

const int N = 1000005;
int fa[N];
void init(int n) {
    for(int i = 1; i <= n; i++) fa[i] = i;
} // the initial situation
int find(int x) {
    if(fa[x] == x) return x;
    return find(fa[x]);
} // get root(x)
bool check(int x, int y) {
    int fx = find(x), fy = find(y);
    return fx == fy;
} // query
void merge(int x, int y) {
    if(check(x, y)) return ;
    fa[find(x)] = find(y);
} // merge and make edge

Note that sometimes you may find that the algorithm is too slow to solve the problems with too large $$$n$$$. For example in an extreme case, that we do M 1 2, and then M 2 3, and then M 3 4, and so on. In this case, finally when you are doing the queries, the graph (or the forest) is degenerated into a list. In this case, if we are querying the bottom of the list, we will get the time complexity of $$$\mathcal O(n^2)$$$.

How to solve this problem in a better way? Let's consider making the traveling while we are find the root of the tree shorter, just point $$$i$$$ direct to $$$\text{root}(i)$$$, then the next time we find the root of the tree, we can find it in $$$\mathcal O(1)$$$ time.

The better find function:

int find(int x) {
    if(fa[x] == x) return x;
    return fa[x] = find(fa[x]);
} // get root(x)

Pay attention to the sentence above: fa[x] = find(fa[x]) returns the value of find(fa[x]) and it makes fa[x] become find(fa[x]). The first usage of it is to travel, the second is to note the root of the vertex, and finally to make the next queries of the same vertex $$$\mathcal O(1)$$$. After that, the graph becomes:

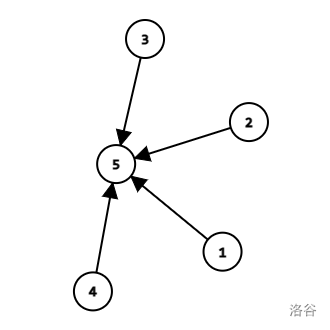
Which looks like a flower:

Picture taken from the Chinese searching website baidu.com.

So we can call it "a flower graph". Querying the root of the vertex in a flower graph takes $$$\mathcal O(1)$$$ time.

Totally the time complexity will be discussed in Part 2.

However, the time complexity still depends on the type of the merging. For fa[u] = v or fa[v] = u may effect the time complexity. There are two ways for us to merge the sets:

1. We consider noting the size of the block(s) which the vertex $$$u,v$$$ belong to. The smaller sized vertex will become the son.

2. We consider noting the depth of the block(s) which the vertex $$$u,v$$$ belong to. The smaller-depth vertex will become the son.

Here is an example implementation for the first way to merge the sets:

void merge(int x, int y) {
    x = find(x), y = find(y);
    if (x == y) return;
    if (size[x] < size[y]) swap(x, y);
    fa[y] = x;
    size[x] += size[y];
}

Both the two versions are easy to implement and the time complexity will be smaller. It'll be discussed in Part 2. These are called heuristic merging.

Part 1: Problems solved using dsu

ABC284C

For each edge x y, just do the operation merge(x, y). Then find all the roots of the vertecies, the count of the roots is the answer.

Part of my code:

int fa[100005];
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
void merge(int x, int y) { fa[find(x)] = find(y); }
//----------------------------------------------------------------
namespace solution{int solve() {
    int n = read<int>(), m=  read<int>();
    for(int i = 1; i <= n; i++) fa[i] = i;
    for(int i = 1; i <= m;i ++) {
        int u = read<int>(), v = read<int>();
        merge(u, v);
    }
    set<int> s; //This is not really necessary.
    for(int i = 1; i <= n; i++) s.insert(find(i));
    write<int>(s.size(), '\n');
    return 0;
}}

Since $$$\text{root}(i)\in [1,n]$$$, then there is no need to use std::set to count the number of the roots, just use an array to count the number of thems is enough.

Extensions for ABC284C

If we are querying the answer of ABC284C when constructing the graph, call the answer cnt, then you can maintain the variable cnt. When merging the vertices, if the vertices've been in the same set already, then cnt remains unchanged. Otherwise, cnt = cnt - 1, since $$$2$$$ sets became $$$1$$$ set.

void merge(int x, int y) {
    if(check(x, y)) return ;
    fa[find(x)] = find(y), cnt--;
} // merge and make edge

Note that the initial value of cnt is the number of vertices, a.k.a. $$$n$$$.

USACO 2010 OCT Silver — Lake Counting

You are given a map of the farm. . stands for land, and W stands for water. Farmer John would like to figure out how many ponds have formed in his field. A pond is a connected set of squares with water in them, where a square is considered adjacent to all eight of its neighbors. Given a diagram of Farmer John's field, determine how many ponds he has.

For example, the map below:

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

Turns out that there are $$$3$$$ ponds.

Solution:

This task seems to have nothing to do with dsu. Then consider how to construct the graph.

If two W squares are adajacent to each other, then you can merge them. After these merging operations are done, we can find out that the answer of ABC284C is the answer we need. Note that you do not need to count the number of elements with ..

You can labelize the squares.

Code

#include<bits/stdc++.h>
#define int long long
using namespace std; 

const int N = 1000005;
int fa[N];
void init(int n) {
    for(int i = 1; i <= n; i++) fa[i] = i;
} // the initial situation
int find(int x) {
    if(fa[x] == x) return x;
    return fa[x] = find(fa[x]);
} // get root(x)
bool check(int x, int y) {
    int fx = find(x), fy = find(y);
    return fx == fy;
} // query
void merge(int x, int y) {
    if(check(x, y)) return ;
    fa[find(x)] = find(y);
} // merge and make edge
char c[105][105];
int n, m;
int d(int i, int j) {
    return (i - 1) * m + j - 1;
}
signed main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m;j ++) {
            cin >> c[i][j];
        }    
    }
    init(n * m + 1);
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(c[i][j] == 'W') {
                if(c[i - 1][j] == 'W' && i != 1) merge(d(i - 1, j), d(i, j));
                if(c[i][j - 1] == 'W' && j != 1) merge(d(i, j - 1), d(i, j));
                if(c[i - 1][j - 1] == 'W' && i != 1 && j != 1) merge(d(i - 1, j - 1), d(i, j));
                if(c[i + 1][j - 1] == 'W' && i != n && j != 1) merge(d(i + 1, j - 1), d(i, j));
                if(c[i + 1][j] == 'W' && i != n) merge(d(i + 1, j), d(i, j));
                if(c[i + 1][j + 1] == 'W' && i != n && j != m) merge(d(i + 1, j + 1), d(i, j));
                if(c[i][j + 1] == 'W'&& j != m) merge(d(i, j + 1), d(i, j));
                if(c[i - 1][j + 1] == 'W' && j != m) merge(d(i - 1, j + 1), d(i, j));
            }
        }
    }
    set<int> s;
    for(int i = 1; i <=n; i++)
        for(int j = 1; j <= m; j++)
            if(c[i][j] == 'W')
                s.insert(find(d(i, j)));
    cout << s.size() << endl;
    return 0;
}

Practice:

Try to turn the 2D problem into a 3D problem.

Code:

#include<bits/stdc++.h>
using namespace std;
const int N = 8001005;
int fa[N];
void init(int n) {
    for(int i = 1; i <= n; i++) fa[i] = i;
} // the initial situation
int find(int x) {
    if(fa[x] == x) return x;
    return fa[x] = find(fa[x]);
} // get root(x)
bool check(int x, int y) {
    int fx = find(x), fy = find(y);
    return fx == fy;
} // query
void merge(int x, int y) {
    if(check(x, y)) return ;
    fa[find(x)] = find(y);
} // merge and make edge
int n, m, h;
int d(int i, int j, int k) {
    i--, j--;
    return k + j * m + i * n * m;
}
signed main() {
    cin >> n >> m >> h;
    vector<vector<string> > v(1);
    for(int i = 1; i <= h; i++) {
        vector<string> tmp(1);
        for(int j = 1; j <= n; j++) {
            string s; cin >> s; s = ' ' + s;
            tmp.push_back(s);
        }
        v.push_back(tmp);
    }
    // puts("done");
    init(n * m * h + 100);
    for(int i = 1; i <= h; i++) {
        for(int j = 1; j <= n; j++) {
            for(int k = 1; k <= m; k++) {
                for(int l = -1; l <= 1; l++) {
                    for(int r = -1; r <= 1; r++) {
                        for(int c = -1; c <= 1; c++) {
                            if(l == 0 && r == 0 && c == 0) continue;
                            if(i + l == 0) continue;
                            if(i + l > h) continue;
                            if(j + r == 0) continue;
                            if(j + r > n) continue;
                            if(k + c == 0) continue;
                            if(k + c > m) continue;
                            if(v[i + l][j + r][k + c] == 'B' && v[i][j][k] == 'B') {
                                merge(d(i, j, k), d(i + l, j + r, k + c));
                            } 
                        }
                    }
                }
            }
        }
    }
    set<int> s;
    for(int i = 1; i <= h; i++)
        for(int j = 1; j <= n; j++)
            for(int k = 1; k <= m; k++)
                if(v[i][j][k] == 'B')
                    s.insert(find(d(i, j, k)));
    cout << s.size() << endl;
    return 0;
}

Part 2 — Time complexity of dsu algorithm

If you are just doing road compression without heuristic merging, the worst time complexity will become $$$\mathcal O(\log n)$$$, the average time complexity is equal to the version with heuristic merging.

If you are doing heuristic merging, the time complexity is below:

We usually call the time complexity of the algorithm $$$\mathcal O(\alpha (n))$$$ when there are $$$n$$$ elements to deal with.

What is $$$\alpha (n)$$$? We know that there is a famous function called Ackermann function, which is:

While $$$\alpha(n)$$$ is the inverse function of the Ackermann function. Ackman functions promote very fast. While $$$\alpha(n)$$$ promotes very slowly.

However, we do not call $$$mathcal O(n\alpha(n))$$$ lineal, but we consider $$$\alpha(n)$$$ a tiny constant.

The proof is using potential energy analysis which may be too hard to understand for beginners. In this case, if you are interested in this analysis, you can search for it on the Internet. We will skip this analysis here.

However, the road compression is doing to many editions and it may effects the time complexity of the algorithm when you are doing the algorithm with segment tree merging or persistent dsu, in this case, we will not use road compression. Instead, heuristic merging is enough.

Part 3 — Another example on dsu

Let's think about a question: dsu can handle many different merging methods. What about splitting and deleting vertices? It's shown that dsu cannot handle splitting sets of vertices in a efficient time complexity. Let's see a simple example below.

Provincial selection contest in China, 2008 — Vertex deletion

Given a graph of vertices $$$1,2,3,\dots, n$$$. Then there are $$$q$$$ following operations:

• Remove a vertex $$$x$$$ from the graph.
• Just after the vertex deletion, answer how many connected blocks are there in the graph.

Solution:

Note that removing a vertex is difficult. Let's consider making the it offline, and to do the whole deletion after reversing the algorithm. Then deletion is turned into addition. Addtion is solvable by dsu, and then we can solve it easily.

Code:

#include <bits/stdc++.h>
#define int long long
const int N = 400005;
int fa[N], cnt = 0;
void init(int n) {
    for(int i = 1; i <= n; i++) fa[i] = i;
} // the initial situation
int find(int x) {
    if(fa[x] == x) return x;
    return fa[x] = find(fa[x]);
} // get root(x)
bool check(int x, int y) {
    int fx = find(x), fy = find(y);
    return fx == fy;
} // query
void merge(int x, int y) {
    if(check(x, y)) return ;
    cnt--;
    fa[find(x)] = find(y);
} // merge and make edge


int u[N], v[N], q[N];
bool ok[N];

using namespace std;

vector<int> G[N];

signed main() {
    int n, m;
    cin >> n >> m;
    init(n);
    cnt = n;
    for(int i = 1; i <= m; i++) {
        cin >> u[i] >> v[i];
        u[i]++, v[i]++;
        G[u[i]].push_back(v[i]);
        G[v[i]].push_back(u[i]);
    }
    int k;
    cin >> k;
    for(int i = 1; i <= k; i++) cin >> q[i], q[i]++, ok[q[i]] = 1;
    int s = 0;
    for(int i = 1; i <= n; i++) {
        if(ok[i]) continue;
        for(auto x : G[i]) {
            if(ok[x]) continue;
            merge(x, i);
            s++;
        }
    }
    stack<int> ans;
    for(int i = k; i; i--) {
        ans.push(cnt - i);
        int x = q[i];
        ok[x] = 0;
        for(auto y : G[x]) {
            if(ok[y]) continue;
            merge(y, x);
            s++;
        }
    }
    // for(int i = 1; i <= m; i++) merge(u[i], v[i]);
    // if(s < m) return 1;
    cout << cnt << endl;
    while(!ans.empty()) {
        cout << ans.top() << endl;
        ans.pop();
    }
    return 0;
}

After solving this problem above, I think you can solve basic problems by using the dsu method, now let's go to further discussion on dsu.

Part 4 — Homework

POJ 2912

link

1417

link

ABC259D — Circumferences

link

CNOI2015 — Algorithm self-analysis

There are many elements $$$e_1,e_2,\dots,e_m$$$ and $$$n$$$ constraints:

• 1 x y, which means that $$$e_x=e_y$$$.
• 2 x y, which means that $$$e_x\not=e_y$$$.

Tell whether there is a solution for $$$e$$$ under the constraints.

$$$1\leq m\leq 10^{12}, 1\leq n\leq 10^6$$$.

CNOI2002 — Legend of Galactic Heroes

There are $$$n$$$ queues $$$Q_1,Q_2,\dots,Q_n$$$. Initially in the $$$Q_i$$$ queue has only one element $$$i$$$. Then you can do operations below:

• M i j, which means to make all the elements in $$$Q_j$$$ pushed into the queue $$$Q_i$$$, which doesn't change the order of the elements in $$$Q_j$$$.
• Q i j, which means to query if $$$i$$$ and $$$j$$$ are in the same queue. If so, then give the distance of the elements.

Part 5: Ending

This blog post explains how to use dsu algorithm. But it's not all what can dsu do. Instead, dsu can be used in many more ways. Next blog we'll discuss problems with dsu algorithm, and more information and ways about dsu merging.

Thanks for reading. If you have any questions, just leave me a comment, i'll check it out.