For even $$$n$$$, a key observation is that $$$x=1,y=\dfrac{n}{2}$$$ is always legit.
And for odd $$$n$$$, notice that $$$x^yy+y^xx=xy(x^{y-1}+y^{x-1})$$$. So if $$$x$$$ or $$$y$$$ is an even number, obviously $$$x^y y+y^x x$$$ is an even number. Otherwise if both $$$x$$$ and $$$y$$$ are all odd numbers , $$$x^{y-1}$$$ and $$$y^{x-1}$$$ are all odd numbers, so $$$x^{y-1}+y^{x-1}$$$ is an even number, and $$$x^yy+y^xx$$$ is also an even number. That means $$$x^yy+y^xx$$$ is always even and there's no solution for odd $$$n$$$.
First, $$$a_i^{p_i}$$$ is equivalent to the product of $$$a_i^{1}$$$ for $$$p$$$ times, so it is sufficient to set all $$$p_i$$$ to $$$1$$$.
Decomposite $$$n$$$ to some prime factors, greedily choose the most number of distinct prime numbers, the product is the maximum.
#include <bits/stdc++.h>
using namespace std;
#define mp make_pair
pair<int, int> s[110];
int d[110];
void get() {
int n, l = 0, i, c;
cin >> n;
for (i = 2; i * i <= n; i++) {
if (n % i == 0) {
c = 0;
while (n % i == 0) c++, n /= i;
s[++l] = make_pair(c, i);
}
}
if (n != 1) s[++l] = make_pair(1, n);
sort(s + 1, s + l + 1), d[l + 1] = 1;
for (i = l; i >= 1; i--) d[i] = d[i + 1] * s[i].second;
int ans = 0;
for (i = 1; i <= l; i++) if (s[i].first != s[i - 1].first) ans += d[i] * (s[i].first - s[i - 1].first);
cout << ans << endl;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
int T;
cin >> T;
while (T--) get();
return 0;
}
This is the reason why the problem was named as Remove the Bracket.
However, We discussed to remove it on 28th Jan in the statement. Really sorry for inconvenience of the statement!
$$$(x_i-s)(y_i-s)\geq 0$$$ tells us either $$$\min(x_i,y_i)\geq s$$$ or $$$\max(x_i,y_i) \leq s$$$, so pickable $$$x_i$$$ is a consecutive range.
Just consider $$$(x_i+y_i)$$$, remove the bracket then it turns to $$$\ldots+ y_{i-1}\cdot x_i+y_i\cdot x_{i+1}+\ldots$$$. When $$$y_{i-1} = x_{i+1}$$$, the result is constant, so we assume that $$$y_{i-1} < x_{i+1}$$$.
If $$$x_i$$$ does not hit the maximum, increase $$$x_i$$$ by $$$1$$$ and decrease $$$y_i$$$ by $$$1$$$, the result will increase by $$$y_{i-1}$$$ and decrease by $$$x_{i+1}$$$, which means decrease by $$$x_{i+1}-y_{i-1}$$$, always better. So $$$x_i$$$ will either hit the maximum or the minimum. Thus, each number has only two ways of rewriting that might be optimal.
This can be done with DP.
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
long long f[N][2],x[N],y[N];
void get() {
int i,n,s,j;
cin>>n>>s;
for(i=1; i<=n; i++) {
cin>>j;
if(i==1||i==n) x[i]=y[i]=j;
else if(j<=s) x[i]=0,y[i]=j;
else x[i]=s,y[i]=j-s;
}
f[1][0]=f[1][1]=0;
for(i=2; i<=n; i++) {
f[i][0]=min(f[i-1][0]+y[i-1]*x[i],f[i-1][1]+x[i-1]*x[i]);
f[i][1]=min(f[i-1][0]+y[i-1]*y[i],f[i-1][1]+x[i-1]*y[i]);
}
cout<<f[n][0]<<endl;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int T; cin>>T;
while(T--) get();
return 0;
}
First, add directed edges from $$$i$$$ to $$$i+a_i$$$. If there's a path from $$$1$$$ to $$$x$$$ satisfying $$$x<1$$$ or $$$x>n$$$, the game end. We consider all nodes $$$x$$$ satisfying $$$x<1$$$ or $$$x>n$$$ to be the end node, and we call the path which starts at node $$$1$$$ until it loops or ends the key path.
If we can end the game at first:
Let's count the opposite — the number of invalid pairs. The graph with the end node forms a tree. Changing edges not on the key path is always legal. If changing the edges on the key path, for node $$$x$$$, we can only change its successor to nodes on the tree with the end node except its precursor or itself.
For the answer, use dfs to count the number of precursors for every nodes on this tree, which is the size of subtree.
If we cannot end the game at first:
We can only change the edge on the key path, redirect them to any nodes on the tree with the end node.
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int a[N], v[N], s[N];
struct E {
int to;
E *nex;
} *h[N];
void add(int u, int v) {
E *cur = new E;
cur->to = v, cur->nex = h[u], h[u] = cur;
}
void dfs(int u) {
s[u] = v[u] = 1;
for (E *cur = h[u]; cur; cur = cur->nex)
dfs(cur->to), s[u] += s[cur->to];
}
void get() {
int i, j, n;
cin >> n;
for (i = 1; i <= n + 1; i++)
s[i] = v[i] = 0, h[i] = 0;
for (i = 1; i <= n; i++) {
cin >> a[i], a[i] = min(i + a[i], n + 1);
if (a[i] <= 0) a[i] = n + 1;
add(a[i], i);
}
dfs(n + 1);
long long ans = 0;
if (v[1] == 1) {
j = 1; do { ans -= s[j] + (n - s[n + 1] + 1), j = a[j]; }
while (j != n + 1);
ans += 1ll * n * (2 * n + 1);
} else {
j = 1; do { ans += (n + s[n + 1]), v[j] = 2, j = a[j]; }
while (v[j] != 2);
}
cout << ans << endl;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int T;
cin >> T;
while (T--) get();
return 0;
}
1787E - The Harmonization of XOR
First, we observe that three subsequences can combine into one, so we only need to care about the maximum number of subsequences.
Make subsequences in the form of $$$[a,a \oplus x]$$$ as much as possible, leave $$$[x]$$$ alone if possible, and the rest becomes a subsequence. This would be optimal.
Proof:
Let $$$B$$$ be the highest bit of $$$x$$$, i.e. the $$$B$$$-th bit of $$$x$$$ is on.
Let $$$M$$$ be the number of numbers from $$$1$$$ to $$$n$$$ satisfying the $$$B$$$-th bit is on.
Then the number of subsequences must be smaller than or equal to $$$M$$$, since there's at least one $$$B$$$-th-bit-on number in each subsequence.
These $$$B$$$-th-bit-on numbers XOR $$$x$$$ must be smaller than themselves, so we can always obtain $$$M$$$ subsequences.
1787F - Inverse Transformation
Consider another question: Given the initial permutation $$$a$$$ and find the permutation $$$a'$$$ on the $$$k$$$-th day?
After a day, element $$$x$$$ will become $$$\sigma(x) = a_x$$$, so we can consider the numbers as nodes, and we add directed edges from $$$x$$$ to $$$a_x$$$. Note that $$$a$$$ is a permutation, so the graph consists of several cycles. After one day, $$$a_x$$$ will become $$$a_{\sigma(x)} = a_{a_x}$$$ -- the second element after $$$x$$$ in the corresponding cycle. Similarly, we can conclude that $$$a_x$$$ will become the $$$2^k$$$-th element after $$$x$$$.
If a cycle $$$c$$$ has an odd length $$$l$$$. Because $$$2^k \bmod l \neq 0$$$, the cycle will never split, the element $$$c_x$$$ will become $$$c_{(x+2^k)\bmod l}$$$ on the $$$k$$$-th day. Otherwise, if a cycle $$$c$$$ has an even length $$$l$$$, after the first day, $$$c_1$$$ will become $$$c_3$$$, $$$c_3$$$ will become $$$c_5$$$, $$$\ldots$$$, $$$c_{2l-1}$$$ will become $$$c_1$$$. And so will the even indices -- that means the original cycle split into two small cycles of the \bf{same size} $$$\dfrac{l}{2}$$$. So, if a cycle of length $$$l = p\cdots 2^q$$$ will split into $$$2^q$$$ small cycles of length $$$p$$$ after exactly $$$q$$$ days.
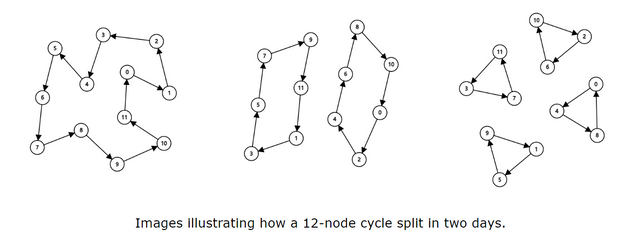
Because the length of a cycle $$$l\le n$$$, so we can perform the transformation for at least $$$\log n$$$ days to split all the cycles of even lengths into cycles of odd lengths. Then we can use our conclusion to calculate the final permutation on the $$$k$$$-th day.
Now let's back to our question. We observed that $$$\sum\limits^n_{i=1} \dfrac{1}{f(i)}$$$ means the number of cycles in the original graph. Then we need to construct the original permutation $$$a$$$ of the least possible cycle. As we've said before, the cycle of length $$$l = p\cdots 2^q$$$ will split into $$$2^q$$$ small cycles of length $$$p$$$ after exactly $$$q$$$ days. So we can count all the cycles in permutation $$$a'$$$.
For cycles of odd length $$$l$$$, we can combine some of them. Specifically, we can combine $$$2^q$$$ cycles into a cycle of length $$$l\cdots 2^q$$$ in the original permutation $$$a$$$. Note that $$$q$$$ must be less than or equal to $$$k$$$.
And for cycles of even length $$$l$$$, we can also combine them. But because they haven't been split on the $$$k$$$-th day, we must combine exactly $$$2^k$$$ cycles. So if the number of these cycles isn't a multiple of $$$2^k$$$, just print \t{NO}.
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int dest[N], visit[N], ans[N], mp[N], ansinv[N], sp;
int pow2(int y, int M) {
long long x = 2, ans = 1;
while (y) {
if (y & 1) ans = ans * x % M;
x = x * x % M, y >>= 1;
}
return ans % M;
}
vector<int> cyc[N];
void get() {
sp = 0;
int n, i, j, m, z, o;
cin >> n >> m;
for (i = 1; i <= n; i++) cyc[i].clear();
for (i = 1; i <= n; i++) visit[i] = 0, cin >> dest[i];
for (i = 1; i <= n; i++) {
if (visit[i]) continue;
j = i, z = 0; do { ++z, visit[j] = 1, j = dest[j]; } while (j != i);
cyc[z].push_back(i);
}
int lim = pow2(min(m, 20), 1e9), s = 0, d, t, num, cp;
for (i = 1; i <= n; i++) {
if (!cyc[i].size()) continue;
int siz = cyc[i].size();
if (i % 2 == 0 && siz % lim) {
cout << "NO" << endl; return;
} else {
cp = -1;
for (j = lim; j > 0; j /= 2) {
while (siz >= j) {
siz -= j, d = s + j * i, t = j;
while (t--) {
++s, ++cp, num = s, o = cyc[i][cp];
do {
ans[num] = o, num += pow2(m, i * j);
if (num > d) num -= j * i;
o = dest[o];
} while (o != cyc[i][cp]);
}
for (int k = sp + 1; k < sp + j * i; k++) mp[k] = k + 1;
mp[sp + j * i] = sp + 1, sp += j * i, s = d;
}
}
}
}
cout << "YES" << endl;
for (i = 1; i <= n; i++) ansinv[ans[i]] = i;
for (i = 1; i <= n; i++) cout << ans[mp[ansinv[i]]] << " \n"[i == n];
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
int T;
cin >> T;
while (T--) get();
return 0;
}
On the original tree, all good paths are constant and one edge can only be on at most one good path.
For each color $$$c$$$, find all edges of color $$$c$$$, and judge if they form a simple path by counting the degree of each node on the path. If so, mark these edges and calculate the length.
When a query changes a node $$$u$$$, several paths across $$$u$$$ are infected.
For example,
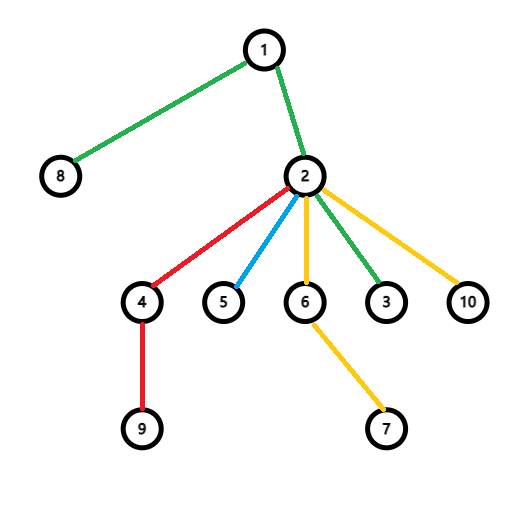
If we are destroying node $$$2$$$, path $$$8-1-2-3$$$, $$$2-4-9$$$, $$$2-5$$$, and $$$7-6-2-10$$$ will not be good paths.
A brute-force solution is to use a priority queue, delete length of bad paths, find the maximum length.
To gain better time complexity, treat two cases of influenced paths separately:
Only one path that goes from the ancestor of $$$u$$$ to its subtree, like $$$8-1-2-3$$$.
All paths whose LCA is $$$u$$$ will be infected, like $$$2-4-9$$$, $$$2-5$$$, and $$$7-6-2-10$$$.
This inspires us to maintain these paths according to their LCAs. That is, use priority queue on every node $$$u$$$ to maintain all paths whose LCA is $$$u$$$.
Then use a global priority queue to maintain the answer of all paths maintained on all nodes.
UPD: An alternative implementation using segment tree comment link.
Have to declare that we built up Problem H from zero. ;)
Since $$$\max (b_i-k_i\cdot t,a_i) = b_i - \min(k_i\cdot t, b_i - a_i)$$$, we can pre-calculate the sum of $$$b_i$$$. Let $$$c_i = b_i - a_i$$$. Now our mission is to minimize the sum of $$$\min(k_i\cdot t, b_i - a_i)$$$.
If we assume $$$\min(k_i\cdot t, b_i - a_i) = k_i\cdot t$$$ for some $$$i$$$, sort these problems in descending order of $$$k_i$$$, then assign $$$1,2,3,\ldots$$$ to their $$$t$$$ in order. For $$$\min(k_i\cdot t, b_i - a_i) = b_i - a_i$$$, they can be directly calculated.
There comes a DP solution: Let $$$f_{i,j}$$$ be the minimum sum, when considering first $$$i$$$ problems (after sorting), $$$j$$$ problems of them satisfying $$$\min(k_i\cdot t, b_i - a_i) = k_i\cdot t$$$.
The time complexity is $$$O(n^2)$$$.
We can find that $$$f_{i,j}$$$ is convex. Proof below:
Let $$$g_{i,j}=f_{i,j}-f_{i,j-1}$$$.
Thus $$$f_{i,j}=f_{i,0}+\sum\limits_{k=1}^jg_{i,k}$$$, rewrite this formula with the original recursive formula.
Then
Let $$$j-1$$$ be $$$j$$$
Subtract the above two formulas from each other
Because $$$k$$$ is monotone non-increasing, so we can use mathematical induction to proof that for $$$j$$$, the increase speed of $$$g_{i-1,j}$$$ is faster than that of $$$k_i\cdot j$$$. We can find a critical value $$$M$$$ that $$$\forall j\le M, g_{i,j}<k_i\cdot j$$$ and $$$\forall j>M,g_{i,j}>k_i\cdot j$$$.
So compared $$$g_i$$$ with $$$g_{i+1}$$$, the first part of the sequence remains unchanged, and the last part is added with $$$k_i$$$, with an additional number $$$k_i\cdot j$$$ in the middle, where $$$j$$$ is the maximum number satisfied $$$g_{i-1,j-1}\le k_i \cdot j$$$.
Use the treap to maintain this sequence, which might be called the slope trick.
First, we observe that: $$$\max\limits_{l>p\,\texttt{or}\,r\leq p}{(\sum\limits_{i=1}^{p}{a_i}+\sum\limits_{i=l}^{r}{a_i})}=\max\limits_{p=1}^{n}{\sum\limits_{i=1}^{p}{a_i}}+\max\limits_{l,r}{\sum\limits_{i=l}^{r}{a_i}}$$$.
Proof: We can proof it by contradiction. Define $$$g(l,r,p)$$$ as $$$\sum\limits_{i=1}^{p}{a_i}+\sum\limits_{i=l}^{r}{a_i}$$$. Suppose $$$l\leq p<r$$$ when $$$g(l,r,p)$$$ hits the maximum value. If $$$\sum\limits_{i=p+1}^{r}{a_i}\geq 0$$$, $$$g(l,r,r)\geq g(l,r,p)$$$, otherwise $$$g(l,p,p)> g(l,r,p)$$$. So the above observation is always correct.
So we can divide the problem into two parts: $$$\max\limits_{p=1}^{n}{\sum\limits_{i=1}^{p}{a_i}}$$$ and $$$\max\limits_{l,r}{\sum\limits_{i=l}^{r}{a_i}}$$$.
For $$$\max\limits_{p=1}^{n}{\sum\limits_{i=1}^{p}{a_i}}$$$, it's easy to solve it by using a stack to calculate the prefix maximum value, and then calculate the answer.
And for $$$\max\limits_{l,r}{\sum\limits_{i=l}^{r}{a_i}}$$$, consider divide and conquer. For a part $$$[l,r]$$$,let $$$m=\lfloor \frac{l+r}{2}\rfloor$$$. Define $$$h(L,R)$$$ as $$$\max\limits_{L\leq l,r\leq R}{\sum\limits_{i=l}^{r}{a_i}}$$$. We want to calculate the sum of $$$h(L,R)$$$ satisfied $$$l\leq L\leq m<R < r$$$. Obviously $$$h(L,R) = \max(\max(h(L,m),h(m+1,R)),\max\limits_{L\leq p\leq m}{\sum\limits_{j=p}^{m}{a_j}}+\max\limits_{m<p\leq R}{\sum\limits_{j=m+1}^{p}{a_j}})$$$, and it's easy to calculate above four value in the time complexity of $$$O(r - l)$$$. We can use binary search to calculate the maximum value. So the problem can be solved in the time complexity of $$$O(n\log ^2n)$$$.
But it's not good enough. We can solve it in the time complexity of $$$O(n\log n)$$$ based on the following theorem:
Define $$$f(p)$$$ as $$$\max\limits_{1\leq q\leq p}{\sum\limits_{i=1}^q{a_i}}$$$. $$$h(1,p)-f(p)$$$ is non-decreasing.
Proof: Actually, if we extend the first theorem, we will find $$$l>p$$$ or $$$r=p$$$ :
If $$$l>p$$$, so $$$\sum\limits_{i=p+1}^r{a_i}<0$$$. When we add an element at the back of the sequence: If $$$\sum\limits_{i=1}^{len}{a_i}>\sum\limits_{i=1}^p{a_i}$$$, $$$p$$$ and $$$r$$$ become $$$len$$$ at the same time. So $$$\Delta f(len)<\Delta h(1,len)$$$ since $$$\sum\limits_{i=p+1}^r{a_i}<0$$$. Otherwise if $$$\sum\limits_{i=1}^{len}{a_i}\leq \sum\limits_{i=1}^p{a_i}$$$, $$$\Delta f(len)=0$$$ while $$$\Delta h(1,len) \geq 0$$$. So the theorem always holds in this circumstance.
If $$$p=r$$$, $$$\Delta f(len)=\Delta h(1,len)$$$, so the theorem holds too.
Because of the theorem, we can replace binary search by two pointers. So the final time complexity is $$$O(n\log n)$$$.
I'm really sorry for the unsatisfactory problems and the tough 3 hours ;)
However, I still hope you can enjoy the problems after the contest. The editorial hasn't been fully checked, so feel free to comment if there're errors, typos or you have questions about them. We'll check them out tomorrow. Thanks!





