Hello Codeforces!
Binary search is useful in many situations. For example, interactive problems or minimizing the maximum problems. Binary search is a good choice when dealing with many situations, and for many binary search problems, monotonousness may be hard to find out and participants may not be able to focus on binary search.
You may think that binary search is simple, but after this blog, you may think more about how binary search is working on competitive programming.
Part A — What is binary search?
Consider the following problem: you are going to guess a number between $$$0$$$ and $$$100$$$, and I'll tell you that the number you give is smaller than the number I thought about or not. How to minimize the number of your guessing?
Well, you may guess $$$50$$$ first, if $$$50$$$ is too large, guess $$$25$$$, otherwise $$$75$$$, and so on. For each guess, you cut off half the possible numbers, since $$$x$$$ is small, the numbers smaller than $$$x$$$ are also small. If $$$x$$$ is large, the numbers larger than $$$x$$$ are also big.
The number of your guessing will be at most $$$\log 100$$$ times. If changed $$$100$$$ to $$$n$$$, the complexity of the guessing will be at most $$$\mathcal O(\log n)$$$.
Why are you using binary search when seeing the problem? Let's consider the following monotonous function $$$f(x)$$$:
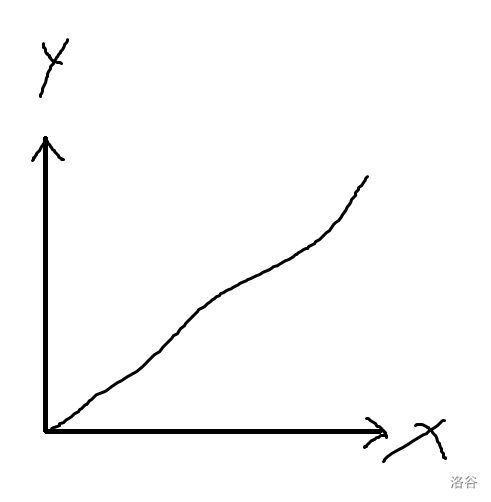
And you are querying the middle place, if too small:
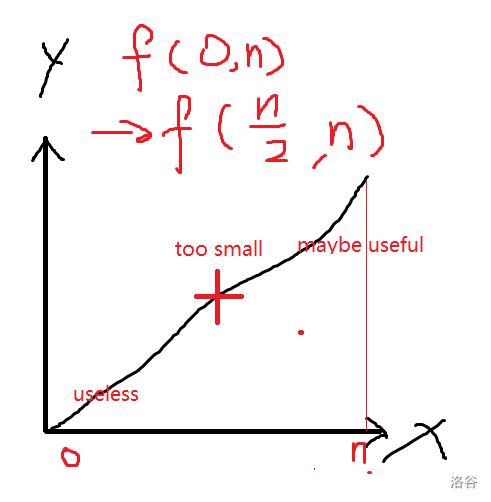
Otherwise, it's just opposite.
This is the motivation for doing binary search. Only if monotonousness is known, binary search can be performed. Otherwise, binary search cannot be performed since the half part cannot be considered useless.
Part B — Implementation
Here we give out a standard code below:
bool chk(int x) {
//something
}
signed main() {
//...
l = 1, r = maxn;
while(l <= r) {
int mid = (l + r) / 2;
if(chk(mid)) l = mid + 1;
else r = mid - 1;
}
cout << l - 1 << endl;
return 0;
}
The final $$$l-1$$$ is the largest value $$$x$$$ with check(x) = 1.
To help understanding, let's write out the guessing number code.
#include<bits/stdc++.h>
#define int long long
using namespace std;
bool chk(int x) {
cout << ">= " << x << endl;
string str; cin >> str;
if(str == "Yes") return 1;
return 0;
}
const int maxn = 100;
signed main() {
int l = 1, r = maxn;
while(l <= r) {
int mid = (l + r) / 2;
if(chk(mid)) l = mid + 1;
else r = mid - 1;
}
cout << "! " << l - 1 << endl;
return 0;
}
For example, we are guessing the number $$$88$$$, this is the process:
>= 50
Yes
>= 75
Yes
>= 88
Yes
>= 94
No
>= 91
No
>= 89
No
! 88
Part C — Basic binary search situations
Task C1
You've got $$$n$$$ trees, the $$$i$$$-th tree has the height of $$$h_i$$$ meters. You are going to cut them. You are going to determine a value $$$x$$$, which is the height of the saw. And then:
- For trees with $$$h_i\ge x$$$, do $$$h_i\gets x$$$, and you will get $$$(h_i-x)$$$ meters of wood.
- For trees with $$$h_i< x$$$, nothing changes.
You want to get $$$m$$$ meters of wood from the trees, to protect the environment, what's the largest $$$x$$$ you can determine?
- $$$1\leq n\leq 10^6$$$
- $$$1\leq h_i\leq 2\times 10^9$$$
Solution of Task C1
It's obvious that, when the $$$x$$$ increases, the length of the wood you get decreases. This means that the monotonousness of the problem is very clear. Due to this, let's do binary search:
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for(int i = (l); i <= (r); i++)
using namespace std;
int A[1000005], n, m;
bool chk(int x) {
int sum = 0;
rep(i, 1, n) {
if(A[i] > x) sum += (A[i] - x);
} return sum >= m;
}
signed main() {
int maxn = 0;
cin >> n >> m;
rep(i, 1, n) {
cin >> A[i];
maxn = max(A[i], maxn);
} int l = 1, r = maxn;
while(l <= r) {
int mid = (l + r) / 2;
if(chk(mid)) l = mid + 1;
else r = mid - 1;
}
cout << l - 1 << endl;
return 0;
}
Task C2
You've got an array $$$a_1,a_2,a_3,\dots,a_n$$$, and you are going to devide the array into $$$m$$$ segments. You are going to minimize the maximum number of the sum of the subsegments.
For example, $$$a=[4, 2, 4, 5, 1], m=3$$$, the answer is $$$6$$$ since $$$[4, 2][4][5, 1]$$$ is possible, and $$$\max(6, 4, 6) = 6$$$ which is the best.
- $$$1\leq m\leq n\leq 10^5$$$.
- $$$0\leq a_i\leq 10^8$$$.
Solution of Task C2
We can find out that, the larger the maxinum is, the fewer segments will be needed. This leads to the monotonousness. And then we can do binary search on the maxinum, and if the mininum needed segments is no more than $$$m$$$, it seems that the mininum can be reached, otherwise it cannot be reached.
So this is the check function:
bool chk(int x) {
int s = 0, ret = 0;
for(int i = 1; i <= n; i++) {
if(s + a[i] > x) ret++, s = 0;
s += a[i];
}
return ret >= m;
}
Complete code example:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int a[200005], n, m;
bool chk(int x) { /* See above */ }
signed main() {
cin >> n >> m;
int sum = 0, maxn = 0;
for(int i = 1; i <= n; i++)
cin >> a[i], sum += a[i], maxn = max(maxn, a[i]);
int l = maxn, r = sum;
while(l <= r) {
int mid = (l + r) / 2;
if(chk(mid)) l = mid + 1;
else r = mid - 1;
}
cout << l << endl;
system("pause");
return 0;
}
Task C3 — [ABC269E] Last Rook
This is an interactive problem.
Solution of Task C3
First, let's think of this picture:

You may find that, the blue part can never been laid a rook, since for each column, there is already a rook. So we have to lay a rook in the red part, and all the blue columns are considered useless.
In implementation, you can always ask the left half of the chessboard. If the result is the same to the numbers of the columns, then the left is useless. Otherwise, the left half is useful. For each query, you can cut off half useless part, so totally you will spend $$$\log n$$$ steps to get the unplaced column.
In the same way, get the unplaced line.
The final complexity of the algorithm is $$$\mathcal O(\log n)$$$.
int solve() {
int n; cin >> n;
int l = 1, r = n;
while(l < r) {
int mid = l + r >> 1;
printf("? %lld %lld %d %lld\n", l, mid, 1, n);
cout << flush;
int x; cin >> x;
if(x != (mid - l + 1)) r = mid;
else l = mid + 1;
}
int ansx = l;
l = 1, r = n;
while(l < r) {
int mid = l + r >> 1;
printf("? %d %lld %lld %lld\n", 1, n, l, mid);
cout << flush;
int x; cin >> x;
if(x != (mid - l + 1)) r = mid;
else l = mid + 1;
}
int ansy = l;
printf("! %lld %lld\n", ansx, ansy);
return 0;
}
Task C4 — sunset
This is an interactive problem.
We have a permutation $$$a$$$ of $$$1,2,3,\dots,n$$$, and another array $$$d$$$ which is the suffix maximum of $$$a$$$.
You can ask the interacter to do the following two operations:
- Tell how many different values are there in $$$d_{1\sim i}$$$.
- Make $$$a_i\gets 0$$$. Note that this may change the array $$$d$$$.
You need to guess out the initial permutation $$$a$$$ within $$$5500$$$ operations, $$$n\leq 500$$$.
Solution of Task C4
First let's think about $$$n\leq 70$$$.
Make $$$\text{ask}(k)$$$ the answer to the first query. It's obvious that:
- $$$d_{i-1}\not=d_{i}$$$
- $$$d_i=d_{i+1}=d_{i+2}=\ldots=d_n$$$
- $$$\text{ask}(i-1)+1=\text{ask}(i)=\text{ask}(n)$$$
Since the monotonousness of $$$d$$$, we can find the first $$$\text{ask}(i)$$$ which fits the $$$\text{ask}(i)=\text{ask}(n)$$$.
This can be solved in $$$\mathcal O(n^2)$$$ queries with $$$n=70$$$ solved. But let's think of the monotonousness of $$$d$$$, we can do a binary search to find the first $$$i$$$ which fits $$$\text{ask}(i)=\text{ask}(n)$$$. Then it's optimized to $$$\mathcal O(n\log n)$$$.
int ask(int n) {
printf("? 1 %d\n", n);fflush(stdout);return read<int>();
}
void chg(int n) {
printf("? 2 %d\n", n);fflush(stdout);
}
vector<int> v;
int ans[505];
void got(int n) {
printf("! ");rep(i, 1, n) print<int>(ans[i], " ");puts("");fflush(stdout);
}
void solve() {
int n = read<int>();
for(int i = n; i >= 1; i--) {
int sum = ask(n);
int l = 1, r = n;
while(l < r) {
int mid = l + ((r - l) >> 1);
if(ask(mid) < sum) l = mid + 1;
else r = mid;
}
ans[l] = i;
if(i > 1) chg(l);
}
got(n);
}





