Problem:

Let $$$n$$$ be a positive integer. A Japanese triangle consists of $$$1 + 2 + \dots + n$$$ circles arranged in an equilateral triangular shape such that for each $$$i = 1$$$, $$$2$$$, $$$\dots$$$, $$$n$$$, the $$$i^{th}$$$ row contains exactly $$$i$$$ circles, exactly one of which is coloured red. A ninja path in a Japanese triangle is a sequence of $$$n$$$ circles obtained by starting in the top row, then repeatedly going from a circle to one of the two circles immediately below it and finishing in the bottom row. Here is an example of a Japanese triangle with $$$n = 6$$$, along with a ninja path in that triangle containing two red circles.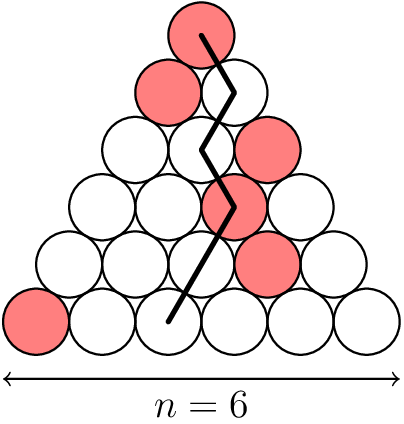

Given a Japanese triangle, find the maximum number of red circles in a ninja path.

I found an algorithm using DP that can solve this problem in $$$O(n^2)$$$. Is there a more efficient solution?