FYI — Its a Netcore Round-2 Question, contest is already over on hackerearth. =================================================================================

Text format of above photo

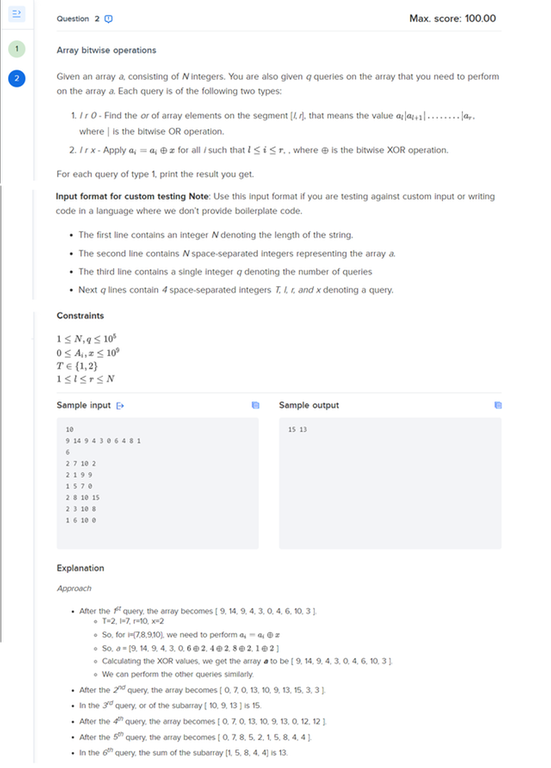
Given an array a, consisting of N integers. You are also given q queries on the array that you need to perform on the array a. Each query is of the following two types:
1. l r 0 - Find the or of array elements on the segment [l, r], that means the value a[l] | a[l+1] | . . . | a[r] where | is the bitwise OR operation.
2. l r x - Apply ai = ai ⊕ x for all i such that l ≤ i ≤r, where ⊕ is the bitwise XOR operation.

For each query of type 1, print the result you get.

Input format for custom testing Note: Use this input format if you are testing against custom input or writing code in a language where we don\'t provide boilerplate code.
• The first line contains an integer N denoting the length of the string.
• The seconf line contains N space-separated integers representing the array a.
• The third line contains a single integer q denoting the number of queries
• Next q lines contain 4 space-separated integers T, l, r, and x denoting a query.


Constraints
1 ≤ N, q ≤ 10^5
0 ≤ Ai, x ≤ 10^9
1 ≤ l ≤ r ≤ N

Sample input:
10
9 14 9 4 3 0 6 4 8 1
6
2 7 10 2
2 1 9 9
1 5 7 0
2 8 10 15
2 3 10 8
1 6 10 0
Sample output
15 13

Explanation
Approach
• After the 1st query, the array becomes [ 9, 14, 9, 4, 3, 0, 4, 6, 10, 3 ].
	o T=2, l=7, r=10, x=2
	o So, for i=[7,8,9,10], we need to perform ai = ai ⊕ x
	o So, a= [9, 14, 9, 4, 3, 0, 6⊕2, 4⊕2,8⊕2, 1⊕2]
	o Calculating the XOR values, we get the array a to be [ 9, 14, 9, 4, 3, 0, 4, 6, 10, 3 ].
	o We can perform the other queries similarly.
• After the 2nd query, the array becomes [ 0, 7, 0, 13, 10, 9, 13, 15, 3, 3 ].
• In the 3rd query, or of the subarray [ 10, 9, 13 ] is 15.
• After the 4th query, the array becomes [0, 7, 0, 13, 10, 9, 13, 0, 12, 12 ].
• After the 5th query, the array becomes [ 0, 7, 8, 5, 2, 1, 5, 8, 4, 4 ].
• In the 6th query, the sum of the subarray [1, 5, 8, 4, 4] is 13.