I'm sorry about my poor English. And I made a mistake that I reverse $n$ and $m$. In this blog, $n\le 10^5$, $m\le 10$, $1\le l\le r\le n$. ↵
↵
This is a online determined algorithm.↵
↵
First, make every cross a vertex. Give each vertex a position $(x, y)$. The position of a vertex equals to the position of the character on its right down side. There is an edge between two vertexes if and only if $|x_1-x_2|+|y_1-y_2|=1$ and the edge splits two **different** characters. ↵
↵
If a vertex doesn't have any edge, remove it.↵
↵
For example, for the example situation in the problem. ↵
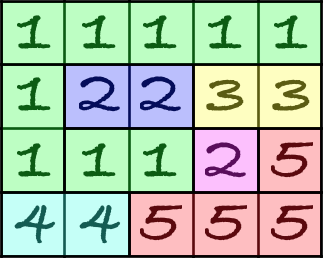 ↵
We will get the graph: ↵
 ↵
When calculating the answer of a range $[l,r]$, it is just like adding edges at the column of $x=l$, the column of $x=r+1$, and removing all the edges out of $[l,r+1]$. For example, we need to calculate the answer in range $[2,4]$ in the previous graph. We just need to calculate the number of "faces" in the remaining graph. ↵
 ↵
Define F as the number of faces(excluding the outside face), E as the number of edges, V as the number of vertexes. Then: ↵
Lemma 1: $V-E+F=1$ holds for each connected planar graph. ↵
↵
<spoiler summary="Proof"> ↵
↵
If there are any vertexes with only $1$ degree left, remove it with it's only edge. $V-E$ remains unchanged after the operation.↵
If there are any faces left, remove any edge on a loop, then the number of faces reduced by $1$. $-E+F$ remains unchanged after the operation.↵
At last, there will be a single vertex without any edge or face. Obviously, $V=1,E=F=0$ so $V-E+F=1$ holds. ↵
↵
</spoiler>↵
↵
↵
↵
For any planar graph, make summation for both sides of $V-E+F=1$ between different connected blocks. We get $\sum V_i -\sum E_i + \sum F_i = \sum 1$, means $V-E+F=C$, where $C$ is the number of connected blocks. ↵
In order to find the value of $F$, we can find the values of $V,E,C$. ↵
↵
Define $V_i$ as the number of vertexes with just right $i$ degree(s). From the rule of building the graph, we can find that only $i\in \{2,3,4\}$, can $V_i>0$. ↵
$F=E-V+C$, so $F=E-V_2-V_3-V_4+C$. Notice that one edge contributes two degrees. So $E=\frac{\sum_i iV_i}{2}$ holds for any graph. For our planar graph, $F=\frac{2V_2+3V_3+4V_4}{2}-V_2-V_3-V_4+C$ holds. It equals to $F=\frac{V_3+2V_4}{2}+C$. ↵
↵
There won't be any vertexes with $4$ degrees on the any side of the range because all edges outboard are removed. ↵
We can get the prefix sum in row to calc the sum of $V_3+2V_4$ in each column. On the both sides, each pair of different adjacent characters causes a vertex with $3$ degrees, so we can the sum of each column. ↵
Then $\frac{V_3+2V_4}{2}$ can be calculated in $\mathcal{O}(1)$ steps for each query. ↵
↵
For a connected block in the cut graph, it can either be connected with the edges added, or be independent. The number of the former is always $1$. For the latter, each block MUST be an independent connected block in the original graph. If it takes vertexes from $x=l_0$ to $x=r_0$, when the query is $[l,r]$, it can be independent if and only if both $l<l_0$ and $r>r_0$ hold. ↵
↵
We can dfs to find all the connected blocks in the original graph. There will be several pairs $(l_i,r_i)$, describing one block each pair. ↵
You can use segment tree to solve it offline with $\mathcal{O}(\log q + \log n)$ steps each query. ↵
↵
Lemma 2: $\sum_i(r_i-l_i+1)=\mathcal{O}(nm)$. ↵
↵
<spoiler summary=Proof> ↵
↵
Each block is connected. If it has any vertex on $x=t-1$ and $x=t+1$, then it must have vertex(es) on $x=t$, because $|(t-1)-(t+1)|+|y_1-y_2|\ge 2$ so we didn't build any edge between $x=t-1$ and $x=t+1$. The block must be connected, so this holds. ↵
In the same way, when it has vertexes on both $x=l$ and $x=r$, it must have vertex(es) on any $l<x<r$. In the other hand, it takes $r-l+1$ vertex at least. Because one vertex can be taken by no more than one block, so the number of taken vertexes can not be less than $\sum_i r_i-l_i+1$ or more than $(n+1)(m+1)$. So the lemma holds.↵
↵
</spoiler> ↵
↵
Consider that $\sum_i [l<l_i<=r_i<r]=\frac{1}{2}\sum_i ([l<l_i<r]+[l<r_i<r]-[l_i\le l<r_i]-[l_i<r\le r_i]+2[l_i\le l\le r\le r_i])$. It is easy to calculate first four items in $\mathcal{O}(1)$ for each query with prefix sum algorithm. ↵
↵
We can treat segment information as binary numbers. We can create a sequence $f$ with $n+1$ numbers, and with $\mathcal{O}(m)$ bits in each number(it can be proved that it is enough to have $m$ bits each). Then, we distribute a $p_i$ to each $(l_i,r_i)$, satisfies $\forall r_i+1=l_j, p_i\neq p_j$. Then we set the $p_i$-th bit of the $x$-th number to $1$ for all the $l_i\le x\le r_i$. We can do this one-by-one by the limit of $\sum_i r_i-l_i+1$. Concretely, we can use bucket sort to sort $(l_i,r_i)$ to make $l_i$ non-decrease in $\mathcal{O}(n)$ steps. Then solve from left to right, record bits are taken in $2$ columns before and bits are not. ↵
↵
There is an $i$ satisfies $l_i\le l\le r\le r_i$ if and only if $\forall l\le j\le r, f_{j,p_i}$ is $1$. In the other hand, the number of $i$ satisfies $l_i\le l\le r\le r_i$ equals to $\operatorname{popcount}(\Large \And _{i=l}^{r} f_i)$. ↵
↵
We just need a data structure to maintain a sequence $\{a_n\}$ satisfies $0\le a_i\le 2^m$, with $\mathcal{O}(nm)$ steps preprocess and $\mathcal{O}(1)$ steps to calculate the bitwise and sum of a range. ↵
Fortunately, there is a data structure called [sqrt tree](https://cp-algorithms.com/data_structures/sqrt-tree.html), can solve the problem in $O(n\log \log n)$ — $O(1)$ steps. So, when $m>\log \log n$, the problem is solved. ↵
↵
To solve situations $m$ is small, we can divide the sequence into blocks. The length of each block is $b$. The situations of numbers in one block cannot over $2^{mb}$. We can compress numbers in a block into one number, and create a table, reflect situations to the and sum. The preprocess has $\mathcal{O}(2^mb)$ steps. ↵
↵
When the query is $[l, r]$, we actually calculate the and sum of $[l,cb],[cb+1,(c+1)b+1],\dots,[db+1,r]$. We build a sqrt tree for a sequence $g$ that $g_i=\Large \And _{j=(i-1)b+1}^{ib}$. The length of $g$ is $\frac{n}{b}$, and the preprocess has $\mathcal{O}(\frac{n}{b}\log \log\frac{n}{b})$ not over $\mathcal{O}(\frac{n}{b}\log\log n)$. Dividing $l$ and $r$ by $b$ helps us get $c$ and $d$ in $\mathcal{O(1)}$. ↵
When we calculating the and sum of $[l,cb]$, we can bitwise or $g_c$ with $2^{bm}-2^{(cb-l+1)m}$, such that $a_i$ satisfies $(c-1)b\le i<l$ has no influence on the result. Because of the bitwise operations, the process just need $\mathcal{O(1)}$ steps. In the same way we can calculate $[db+1, r]$. ↵
↵
The time complexity of the data structure is $\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$ — $\mathcal{O}(1)$. When $m<\frac{\log n}{\log\log n}$, we get $b=\log\log n$ that $\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$ is no more than $\mathcal{O}(n)$, obviously less than $\mathcal{O}(nm)$. ↵
↵
So we solved 811E or #462 E in $\mathcal{O(nm+q)}$, and the algorithm is online. ↵
↵
[Accepted Code](https://codeforces.net/contest/811/submission/250517393)
↵
This is a online determined algorithm.↵
↵
First, make every cross a vertex. Give each vertex a position $(x, y)$. The position of a vertex equals to the position of the character on its right down side. There is an edge between two vertexes if and only if $|x_1-x_2|+|y_1-y_2|=1$ and the edge splits two **different** characters. ↵
↵
If a vertex doesn't have any edge, remove it.↵
↵
For example, for the example situation in the problem. ↵
 ↵
We will get the graph: ↵
 ↵
When calculating the answer of a range $[l,r]$, it is just like adding edges at the column of $x=l$, the column of $x=r+1$, and removing all the edges out of $[l,r+1]$. For example, we need to calculate the answer in range $[2,4]$ in the previous graph. We just need to calculate the number of "faces" in the remaining graph. ↵
 ↵
Define F as the number of faces(excluding the outside face), E as the number of edges, V as the number of vertexes. Then: ↵
Lemma 1: $V-E+F=1$ holds for each connected planar graph. ↵
↵
<spoiler summary="Proof"> ↵
↵
If there are any vertexes with only $1$ degree left, remove it with it's only edge. $V-E$ remains unchanged after the operation.↵
If there are any faces left, remove any edge on a loop, then the number of faces reduced by $1$. $-E+F$ remains unchanged after the operation.↵
At last, there will be a single vertex without any edge or face. Obviously, $V=1,E=F=0$ so $V-E+F=1$ holds. ↵
↵
</spoiler>↵
↵
↵
↵
For any planar graph, make summation for both sides of $V-E+F=1$ between different connected blocks. We get $\sum V_i -\sum E_i + \sum F_i = \sum 1$, means $V-E+F=C$, where $C$ is the number of connected blocks. ↵
In order to find the value of $F$, we can find the values of $V,E,C$. ↵
↵
Define $V_i$ as the number of vertexes with just right $i$ degree(s). From the rule of building the graph, we can find that only $i\in \{2,3,4\}$, can $V_i>0$. ↵
$F=E-V+C$, so $F=E-V_2-V_3-V_4+C$. Notice that one edge contributes two degrees. So $E=\frac{\sum_i iV_i}{2}$ holds for any graph. For our planar graph, $F=\frac{2V_2+3V_3+4V_4}{2}-V_2-V_3-V_4+C$ holds. It equals to $F=\frac{V_3+2V_4}{2}+C$. ↵
↵
There won't be any vertexes with $4$ degrees on the any side of the range because all edges outboard are removed. ↵
We can get the prefix sum in row to calc the sum of $V_3+2V_4$ in each column. On the both sides, each pair of different adjacent characters causes a vertex with $3$ degrees, so we can the sum of each column. ↵
Then $\frac{V_3+2V_4}{2}$ can be calculated in $\mathcal{O}(1)$ steps for each query. ↵
↵
For a connected block in the cut graph, it can either be connected with the edges added, or be independent. The number of the former is always $1$. For the latter, each block MUST be an independent connected block in the original graph. If it takes vertexes from $x=l_0$ to $x=r_0$, when the query is $[l,r]$, it can be independent if and only if both $l<l_0$ and $r>r_0$ hold. ↵
↵
We can dfs to find all the connected blocks in the original graph. There will be several pairs $(l_i,r_i)$, describing one block each pair. ↵
You can use segment tree to solve it offline with $\mathcal{O}(\log q + \log n)$ steps each query. ↵
↵
Lemma 2: $\sum_i(r_i-l_i+1)=\mathcal{O}(nm)$. ↵
↵
<spoiler summary=Proof> ↵
↵
Each block is connected. If it has any vertex on $x=t-1$ and $x=t+1$, then it must have vertex(es) on $x=t$, because $|(t-1)-(t+1)|+|y_1-y_2|\ge 2$ so we didn't build any edge between $x=t-1$ and $x=t+1$. The block must be connected, so this holds. ↵
In the same way, when it has vertexes on both $x=l$ and $x=r$, it must have vertex(es) on any $l<x<r$. In the other hand, it takes $r-l+1$ vertex at least. Because one vertex can be taken by no more than one block, so the number of taken vertexes can not be less than $\sum_i r_i-l_i+1$ or more than $(n+1)(m+1)$. So the lemma holds.↵
↵
</spoiler> ↵
↵
Consider that $\sum_i [l<l_i<=r_i<r]=\frac{1}{2}\sum_i ([l<l_i<r]+[l<r_i<r]-[l_i\le l<r_i]-[l_i<r\le r_i]+2[l_i\le l\le r\le r_i])$. It is easy to calculate first four items in $\mathcal{O}(1)$ for each query with prefix sum algorithm. ↵
↵
We can treat segment information as binary numbers. We can create a sequence $f$ with $n+1$ numbers, and with $\mathcal{O}(m)$ bits in each number(it can be proved that it is enough to have $m$ bits each). Then, we distribute a $p_i$ to each $(l_i,r_i)$, satisfies $\forall r_i+1=l_j, p_i\neq p_j$. Then we set the $p_i$-th bit of the $x$-th number to $1$ for all the $l_i\le x\le r_i$. We can do this one-by-one by the limit of $\sum_i r_i-l_i+1$. Concretely, we can use bucket sort to sort $(l_i,r_i)$ to make $l_i$ non-decrease in $\mathcal{O}(n)$ steps. Then solve from left to right, record bits are taken in $2$ columns before and bits are not. ↵
↵
There is an $i$ satisfies $l_i\le l\le r\le r_i$ if and only if $\forall l\le j\le r, f_{j,p_i}$ is $1$. In the other hand, the number of $i$ satisfies $l_i\le l\le r\le r_i$ equals to $\operatorname{popcount}(\Large \And _{i=l}^{r} f_i)$. ↵
↵
We just need a data structure to maintain a sequence $\{a_n\}$ satisfies $0\le a_i\le 2^m$, with $\mathcal{O}(nm)$ steps preprocess and $\mathcal{O}(1)$ steps to calculate the bitwise and sum of a range. ↵
Fortunately, there is a data structure called [sqrt tree](https://cp-algorithms.com/data_structures/sqrt-tree.html), can solve the problem in $O(n\log \log n)$ — $O(1)$ steps. So, when $m>\log \log n$, the problem is solved. ↵
↵
To solve situations $m$ is small, we can divide the sequence into blocks. The length of each block is $b$. The situations of numbers in one block cannot over $2^{mb}$. We can compress numbers in a block into one number, and create a table, reflect situations to the and sum. The preprocess has $\mathcal{O}(2^mb)$ steps. ↵
↵
When the query is $[l, r]$, we actually calculate the and sum of $[l,cb],[cb+1,(c+1)b+1],\dots,[db+1,r]$. We build a sqrt tree for a sequence $g$ that $g_i=\Large \And _{j=(i-1)b+1}^{ib}$. The length of $g$ is $\frac{n}{b}$, and the preprocess has $\mathcal{O}(\frac{n}{b}\log \log\frac{n}{b})$ not over $\mathcal{O}(\frac{n}{b}\log\log n)$. Dividing $l$ and $r$ by $b$ helps us get $c$ and $d$ in $\mathcal{O(1)}$. ↵
When we calculating the and sum of $[l,cb]$, we can bitwise or $g_c$ with $2^{bm}-2^{(cb-l+1)m}$, such that $a_i$ satisfies $(c-1)b\le i<l$ has no influence on the result. Because of the bitwise operations, the process just need $\mathcal{O(1)}$ steps. In the same way we can calculate $[db+1, r]$. ↵
↵
The time complexity of the data structure is $\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$ — $\mathcal{O}(1)$. When $m<\frac{\log n}{\log\log n}$, we get $b=\log\log n$ that $\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$ is no more than $\mathcal{O}(n)$, obviously less than $\mathcal{O}(nm)$. ↵
↵
So we solved 811E or #462 E in $\mathcal{O(nm+q)}$, and the algorithm is online. ↵
↵
[Accepted Code](https://codeforces.net/contest/811/submission/250517393)





