I'm sorry about my poor English. And I made a mistake that I reverse $$$n$$$ and $$$m$$$. In this blog, $$$n\le 10^5$$$, $$$m\le 10$$$, $$$1\le l\le r\le n$$$.

This is a online determined algorithm.

First, make every cross a vertex. Give each vertex a position $$$(x, y)$$$. The position of a vertex equals to the position of the character on its right down side. There is an edge between two vertexes if and only if:
- $$$|x_1-x_2|+|y_1-y_2|=1$$$
- The edge splits two different characters.

If a vertex doesn't have any edge, remove it.

For example, for the example situation in the problem.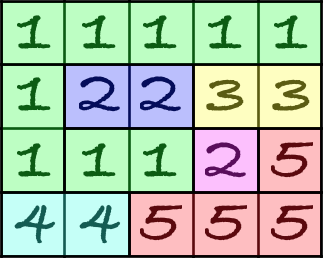

We will get the graph: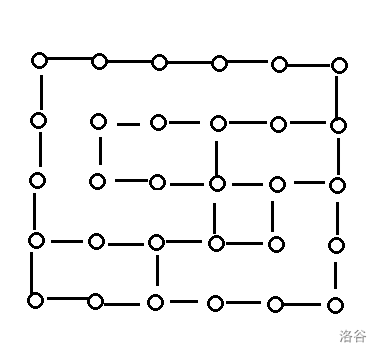

When calculating the answer of a range $$$[l,r]$$$, it is just like adding edges at the column of $$$x=l$$$, the column of $$$x=r+1$$$, and removing all the edges out of $$$[l,r+1]$$$. For example, we need to calculate the answer in range $$$[2,4]$$$ in the previous graph. We just need to calculate the number of "faces" in the remaining graph.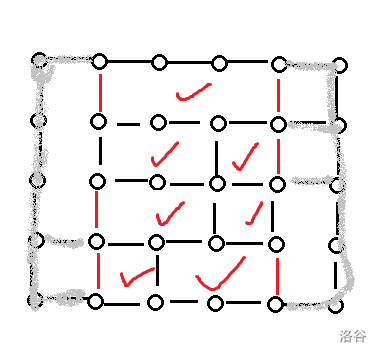

Define F as the number of faces(excluding the outside face), E as the number of edges, V as the number of vertexes. Then:
Lemma 1: $$$V-E+F=1$$$ holds for each connected planar graph.

For any planar graph, make summation for both sides of $$$V-E+F=1$$$ between different connected blocks. We get $$$\sum V_i -\sum E_i + \sum F_i = \sum 1$$$, means $$$V-E+F=C$$$, where $$$C$$$ is the number of connected blocks.
In order to find the value of $$$F$$$, we can find the values of $$$V,E,C$$$.

Define $$$V_i$$$ as the number of vertexes with just right $$$i$$$ degree(s). From the rule of building the graph, we can find that only $$$i\in {2,3,4}$$$, can $$$V_i>0$$$. $$$F=E-V+C$$$, so $$$F=E-V_2-V_3-V_4+C$$$. Notice that one edge contributes two degrees. So $$$E=\frac{\sum_i iV_i}{2}$$$ holds for any graph. For our planar graph, $$$F=\frac{2V_2+3V_3+4V_4}{2}-V_2-V_3-V_4+C$$$ holds. It equals to $$$F=\frac{V_3+2V_4}{2}+C$$$.

There won't be any vertexes with $$$4$$$ degrees on the any side of the range because all edges outboard are removed.
We can get the prefix sum in row to calc the sum of $$$V_3+2V_4$$$ in each column. On the both sides, each pair of different adjacent characters causes a vertex with $$$3$$$ degrees, so we can the sum of each column.
Then $$$\frac{V_3+2V_4}{2}$$$ can be calculated in $$$\mathcal{O}(1)$$$ steps for each query.

For a connected block in the cut graph, it can either be connected with the edges added, or be independent. The number of the former is always $$$1$$$. For the latter, each block MUST be an independent connected block in the original graph. If it takes vertexes from $$$x=l_0$$$ to $$$x=r_0$$$, when the query is $$$[l,r]$$$, it can be independent if and only if both $$$l<l_0$$$ and $$$r>r_0$$$ hold.

We can dfs to find all the connected blocks in the original graph. There will be several pairs $$$(l_i,r_i)$$$, describing one block each pair.
You can use segment tree to solve it offline with $$$\mathcal{O}(\log q + \log n)$$$ steps each query.

Lemma 2: $$$\sum_i(r_i-l_i+1)=\mathcal{O}(nm)$$$.

Each block is connected. If it has any vertex on $$$x=t-1$$$ and $$$x=t+1$$$, then it must have vertex(es) on $$$x=t$$$, because $$$|(t-1)-(t+1)|+|y_1-y_2|\ge 2$$$ so we didn't build any edge between $$$x=t-1$$$ and $$$x=t+1$$$. The block must be connected, so this holds.
In the same way, when it has vertexes on both $$$x=l$$$ and $$$x=r$$$, it must have vertex(es) on any $$$l<x<r$$$. In the other hand, it takes $$$r-l+1$$$ vertex at least. Because one vertex can be taken by no more than one block, so the number of taken vertexes can not be less than $$$\sum_i r_i-l_i+1$$$ or more than $$$(n+1)(m+1)$$$. So the lemma holds.

Consider that $$$\sum_i [l<l_i<=r_i<r]=\frac{1}{2}\sum_i ([l<l_i<r]+[l<r_i<r]-[l_i\le l<r_i]-[l_i<r\le r_i]+2[l_i\le l\le r\le r_i])$$$. It is easy to calculate first four items in $$$\mathcal{O}(1)$$$ for each query with prefix sum algorithm.

We can treat segment informations as binary numbers. We can create a sequence $$$f$$$ with $$$n+1$$$ numbers, and with $$$\mathcal{O}(m)$$$ bits in each number(it can be proved that it is enough to have $$$m$$$ bits each). Then, we distribute a $$$p_i$$$ to each $$$(l_i,r_i)$$$, satisfies $$$\forall r_i+1=l_j, p_i\neq p_j$$$. Then we set the $$$p_i$$$-th bit of the $$$x$$$-th number to $$$1$$$ for all the $$$l_i\le x\le r_i$$$. We can do this one-by-one by the limit of $$$\sum_i r_i-l_i+1$$$. Concretely, we can use bucket sort to sort

Unable to parse markup [type=CF_MATHJAX]

Unable to parse markup [type=CF_MATHJAX]

There is an $$$i$$$ satisfies $$$l_i\le l\le r\le r_i$$$ if and only if $$$\forall l\le j\le r, f_{j,p_i}$$$ is $$$1$$$. In the other hand, the number of $$$i$$$ satisfies $$$l_i\le l\le r\le r_i$$$ equals to $$$\operatorname{popcount}(\Large &amp; _{i=l}^{r} f_i)$$$.

We just need a data structure to maintain a sequence $$${a_n}$$$ satisfies $$$0\le a_i\le 2^m$$$, with $$$\mathcal{O}(nm)$$$ steps pretreatment and $$$\mathcal{O}(1)$$$ steps to calculate the bitwise and sum of a range.
Fortunately, there is a data structure called sqrt tree, can solve the problem in $$$O(n\log \log n)$$$ — $$$O(1)$$$ steps. So, when $$$m>\log \log n$$$, the problem is solved.

To solve situations $$$m$$$ is small, we can divide the sequence into blocks. The length of each block is $$$b$$$. The situations of numbers in one block cannot over $$$2^{mb}$$$. We can compress numbers in a block into one number, and create a table, reflect situations to the and sum. The pretreatment has $$$\mathcal{O}(2^mb)$$$ steps.

When the query is $$$[l, r]$$$, we actually calculate the and sum of $$$[l,cb],[cb+1,(c+1)b+1],\dots,[db+1,r]$$$. We build a sqrt tree for a sequence $$$g$$$ that $$$g_i=\Large &amp; _{j=(i-1)b+1}^{ib}$$$. The length of $$$g$$$ is $$$\frac{n}{b}$$$, and the pretreatment has $$$\mathcal{O}(\frac{n}{b}\log \log\frac{n}{b})$$$ not over $$$\mathcal{O}(\frac{n}{b}\log\log n)$$$. Dividing $$$l$$$ and $$$r$$$ by $$$b$$$ helps us get $$$c$$$ and $$$d$$$ in $$$\mathcal{O(1)}$$$.
When we calculating the and sum of $$$[l,cb]$$$, we can bitwise or $$$g_c$$$ with $$$2^{bm}-2^{(cb-l+1)m}$$$, such that $$$a_i$$$ satisfies $$$(c-1)b\le i<l$$$ has no influence on the result. Because of the bitwise operations, the process just need $$$\mathcal{O(1)}$$$ steps. In the same way we can calculate $$$[db+1, r]$$$.

The time complexity of the data structure is $$$\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$$$ — $$$\mathcal{O}(1)$$$. When $$$m<\frac{\log n}{\log\log n}$$$, we get $$$b=\log\log n$$$ that $$$\mathcal{O}(\frac{n}{b}\log\log n+2^{mb})$$$ is no more than $$$\mathcal{O}(n)$$$, obviously less than $$$\mathcal{O}(nm)$$$.

So we solved 811E or #462 E in $$$\mathcal{O(nm+q)}$$$, and the algorithm is online.

#include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<cassert>
#define maxn 15
#define maxm 132005
#define AND_ONE 16777215 //2^24-1
#define l2_maxm 18 //log_2 maxm
 
using namespace std;
 
int n, m, q, ql, qr, a[maxn][maxm], sf[maxn][maxm], sr[maxn][maxm], sc[maxn][maxm], vis[maxn][maxm], sl[maxm], usd[maxn], val[maxm];
int l2[(1 << l2_maxm) + 5], cnt[maxm];
 
int lp = maxm - 3, rp = 0, u = maxn, d = 0;
 
const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}, px[4] = {-1, -1, 0, 0}, py[4] = {-1, 0, 0, -1};
 
vector<int> g[maxm], p[maxm];
 
struct sqrt_tree {
	int n, m, dat[maxm], sum[maxm][l2_maxm + 1], pre[maxm][l2_maxm + 1], suf[maxm][l2_maxm + 1], b[l2_maxm + 1];
	sqrt_tree() {
		for(int i = 0; i < maxm - 5; i++) {
			dat[i] = AND_ONE;
			for(int j = 0; j < l2_maxm; j++) {
				sum[i][j] = pre[i][j] = suf[i][j] = AND_ONE;
			}
		}
	}
	int build(int *a, int nn) {
		n = nn;
		for(int i = 0; i < n; i++) dat[i] = a[i];
		b[0] = 1;
		m = 0;
		for(int i = 1; b[i - 1] && ((n >> (b[i - 1] << 1))); i++) {
			m = i;
			if(i == 1) b[i] = 1;
			else b[i] = b[i - 1] << 1;
		}
		n = ((n + (1 << b[m]) - 1) >> b[m]) << b[m];
		for(int i = 0; i <= m; i++) {
			for(int j = 0; j < n; j += (1 << b[i])) {
				for(int k = 0; k < (1 << b[i]); k++) {
					sum[j][i] &= dat[j + k];
					pre[j + k][i] = dat[j + k];
					if(k) pre[j + k][i] &= pre[j + k - 1][i];
				}
				for(int k = (1 << b[i]) - 1; k >= 0; k--) {
					suf[j + k][i] = dat[j + k];
					if(k ^ ((1 << b[i]) - 1)) suf[j + k][i] &= suf[j + k + 1][i]; 
				}
				for(int k = 1; k < (1 << b[i]); k++) {
					if(j + (k << b[i]) >= n) break;
					sum[j + k][i] = sum[j + k - 1][i] & sum[j + (k << b[i])][i]; 
				}
			}
		}
		return n;
	}
	int query(int l, int r) {
		int p = l2[l ^ r];
		if(~p) {
			int i = l2[p] + 1;
			if((l >> b[i]) + 1 == (r >> b[i])) return suf[l][i] & pre[r][i];
			else return suf[l][i] & pre[r][i] & sum[(((l + (1 << b[i])) >> b[i]) << b[i]) + (r >> b[i]) - (l >> b[i]) - 2][i];
		}
		else return dat[l];
	} 
} sqt;
 
struct ras {
	int n, dat[maxm], V, mode, dta[maxm], adt[maxm], pre[maxm], suf[maxm], sum[(1 << l2_maxm) + 5], b;
	ras() {
		for(int i = 0; i < maxm - 5; i++) dat[i] = dta[i] = AND_ONE, adt[i] = 0;
		for(int i = 0; i < (1 << l2_maxm); i++) sum[i] = AND_ONE;
	}
	void build(int *a, int nn) {
		n = nn;
		V = 1;
		for(int i = 1; i <= n; i++) V = max(V, a[i]);
		V = ceil(log2(V));
		b = ceil(log2(log2(n)));
		if(V * b >= 30) mode = 1, n = sqt.build(a, nn);
		else {
			mode = 2;
			for(int i = 0; i < n; i++) dat[i] = a[i];
			n = (n + b - 1) / b;
			for(int j = 0; j < n; j++) {
				for(int i = 0; i < b; i++) {
					dta[j] &= dat[j * b + i];
				}
			}
			n = b * sqt.build(dta, n);
			for(int j = 0; j < n; j += b) {
				for(int i = 0; i < b; i++) {
					adt[j] |= dat[i + j] << ((b - i - 1) * V);
					pre[i + j] = dat[i + j];
					if(i) pre[i + j] &= pre[i + j - 1];
				}
				for(int i = b - 1; i >= 0; i--) {
					suf[i + j] = dat[i + j];
					if(i ^ (b - 1)) suf[i + j] &= suf[i + j + 1];
				}
				for(int i = 1; i < b; i++) adt[i + j] = adt[i];
			}
			sum[(1 << (V * b)) - 1] = ((1 << V) - 1);
			int mx = (1 << (V * b));
			for(int i = mx - 2; i >= 0; i--) {
				sum[i] = sum[(i >> V) | (((1 << V) - 1) << ((b - 1) * V))] & i;
			}
		}
	}
	int query(int l, int r) {
		if(mode == 1) return sqt.query(l, r);
		else {
			if(l / b == r / b) {
				return sum[adt[l / b * b] & (((1 << (V * (b - l % b))) - 1) ^ ((1 << (V * (b - r % b - 1))) - 1))];
			}
			else if(l / b + 1 == r / b) {
				return suf[l] & pre[r];
			}
			else return suf[l] & pre[r] & sqt.query(l / b + 1, r / b - 1);
		}
	}
} ra; 
 
void dfs(int i, int j) {
	if(vis[i][j]) {
		return ;
	}
	vis[i][j] = 1;
	lp = min(lp, j), rp = max(rp, j);
	u = min(u, i), d = max(d, i);
	for(int d = 0; d < 4; d++) {
		int x = i + dx[d], y = j + dy[d];
		if(x >= 1 && x <= n + 1 && y >= 1 && y <= m + 1) {
			if(a[i + px[d]][j + py[d]] != a[i + px[(d + 1) & 3]][j + py[(d + 1) & 3]]) {
				dfs(x, y);
			}
		}
	}
}
 
int main() {
	ios::sync_with_stdio(false); cin.tie(0);
	cin >> n >> m >> q;
	l2[0] = -1;
	for(int i = 1; i < (1 << l2_maxm); i++) l2[i] = l2[i >> 1] + 1;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) cin >> a[i][j];
	}
	for(int i = 1; i <= n + 1; i++) {
		for(int j = 1; j <= m + 1; j++) {
			sf[i][j] = (a[i][j] != a[i][j - 1]) + (a[i][j - 1] != a[i - 1][j - 1]) + (a[i - 1][j - 1] != a[i - 1][j]) + (a[i - 1][j] != a[i][j]);
			sr[i][j] = a[i][j] != a[i][j - 1];
			sc[i][j] = a[i][j] != a[i - 1][j];
			if(!vis[i][j] && sf[i][j]) {
				lp = maxm - 3, rp = 0, u = maxn, d = 0;
				dfs(i, j);
				if(lp != 1 && rp != m + 1 && u != 1 && d != n + 1) {
					g[lp].push_back(rp);
					cnt[lp]++, cnt[rp]++;
				}
			}
			sf[i][j] = max(sf[i][j] - 2, 0);
			sf[i][j] += sf[i - 1][j] - sf[i - 1][j - 1] + sf[i][j - 1]; 
			sr[i][j] += sr[i][j - 1];
			sc[i][j] += sc[i - 1][j];
		}
	}
	for(int i = 1; i <= m + 1; i++) {
		cnt[i] += cnt[i - 1];
	}
	for(int i = 1; i <= m + 1; i++) {
		int ptr = 0;
		for(int r : g[i]) {
			while(usd[ptr] && ptr <= n) ptr++;
			if(usd[ptr]) break;
			usd[ptr] = 1;
			p[r + 1].push_back(ptr);
		}
		for(int x : p[i]) usd[x] = 0;
		for(int j = 0; j <= n; j++) {
			val[i] |= (usd[j] << j);
		}
	}
	val[0] = AND_ONE;
	ra.build(val, m + 2);
	while(q--) {
		cin >> ql >> qr;
		int ans = sf[n][qr] - sf[n][ql] + sf[1][ql] - sf[1][qr];
		ans += sc[n][qr] - sc[1][qr] + sc[n][ql] - sc[1][ql];
		ans += sr[n][qr] - sr[n][ql] + sr[1][qr] - sr[1][ql];
		if(ql != qr) {
			ans += cnt[qr] - cnt[ql];
			ans -= __builtin_popcount(val[ql] & val[ql + 1]) + __builtin_popcount(val[qr] & val[qr + 1]);
			ans += 2 * __builtin_popcount(ra.query(ql, qr + 1) & ((1 << (n + 1)) - 1));
		}
		cout << (ans >> 1) + 1 << '\n';
	}
}