For Alice, what if choosing the maximum value doesn't work?

Consider parity.

Case $$$1$$$: When all values appear an even number of times, Alice will lose. This is because no matter which number Alice chooses, Bob can mimic Alice's move.

Case $$$2$$$: When at least one value appears an odd number of times, Alice will win. Alice only needs to choose the maximum value that appears an odd number of times, which will force Bob into Case $$$1$$$.

Time complexity: $$$O(n)$$$.

Sort the array $$$a$$$ in non-increasing order. We can observe that any state can be represented as a prefix of the array $$$a$$$. Consider dynamic programming: let $$$dp_i$$$ denote whether the first player is guaranteed to win when the state is $$$a_{1...i}$$$ ($$$dp_i=1$$$ indicates a guaranteed win for the first player). We have the following formula:

• $$$dp_1=1$$$;

• $$$dp_i= \sim (dp_{i-1}$$$ & $$$dp_{id_1-1}$$$ & $$$dp_{id_2-1} \ldots)$$$, where $$$id_j$$$ satisfies $$$a_{id_j} \neq a_{id_j+1}$$$ and $$$id_j < i$$$.

Time complexity: $$$O(n^2)$$$.

#include <bits/stdc++.h>
using namespace std;
#define m_p make_pair
#define all(x) (x).begin(),(x).end()
#define sz(x) ((int)(x).size())
#define fi first
#define se second
typedef long long ll;
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
mt19937 rnf(2106);
const int N = 55;

int n;
int q[N];

void solv()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        q[i] = 0;
    for (int i = 1; i <= n; ++i)
    {
        int x;
        cin >> x;
        ++q[x];
    }

    for (int i = 1; i <= n; ++i)
    {
        if (q[i] % 2 == 1)
        {
            cout << "YES\n";
            return;
        }
    }
    cout << "NO\n";
}

int main()
{
    #ifdef SOMETHING
    freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    #endif // SOMETHING
    ios_base::sync_with_stdio(false), cin.tie(0);

    int tt = 1;
    cin >> tt;
    while (tt--)
    {
        solv();
    }
    return 0;
}

Starting from a trival construction.

Adjust it.

First, we consider making $$$presum_x > presum_j$$$ for all $$$x < i \le n$$$, and similarly for $$$y$$$. We can think of a trivial construction: $$$a[r, \ldots ,l]=[1, \ldots ,1], a[1, \ldots...,r-1]=[-1, \ldots, -1]$$$ and $$$a[l+1,\ldots,n]=[-1, \ldots, -1]$$$.

The construction doesn't works when $$$presum_x<0$$$, but we are close to the correct solution. Next, we will make a little adjustment: $$$a[r, \ldots, l]=[1,\ldots,1], a[1, \ldots...,r-1]=[\ldots,1, -1]$$$ and $$$a[l+1,\ldots,n]=[-1,1, \ldots]$$$.

It is not hard to see $$$presum_x \ge presum_j$$$ for all $$$x < i \le n$$$, and for $$$1 \le i \le y$$$, $$$\max(presum_i)-min(presum_i)\le 1$$$. Thus, we get $$$presum_x \ge 2+presum_{y-1} \ge 2+min(presum_i) \ge 1+max(presum_i)$$$. The same applies to the suffix sum as well. Therefore, this construction is valid.

Time complexity: $$$O(n)$$$.

#include<bits/stdc++.h>

using namespace std;

int main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int t;
  cin >> t;
  while(t>0){
    t--;
    int n,x,y;
    cin >> n >> x >> y;
    x--; y--;
    vector<int> a(n,1);
    int e;
    e=-1;
    for(int i=x+1;i<n;i++){
      a[i]=e;
      e*=-1;
    }
    e=-1;
    for(int i=y-1;i>=0;i--){
      a[i]=e;
      e*=-1;
    }
    for(int i=0;i<n;i++){
      if(i){cout << " ";}
      cout << a[i];
    }cout << "\n";
  }
  return 0;
}

After one operation, the array becomes non-decreasing.

Consider $$$a_1=a_2=\ldots=a_n$$$, the operation seems to have shifted the array right.

When does the "right shift" parttern happen?

Read hints first.

Let's consider only non-decreasing arrays. Observe a continuous segments $$$a[l...r]=x(l<r,x>0)$$$, after one operation, we get $$$a[l+1,min(r+1,n)]=x$$$ holds. We can conclude that if, for all non-zero contiguous segments in the array (except the last one), their lengths are all greater than $$$1$$$, then the array follows the "right shift" parttern. Let's say this kind of array "good".

The last problem is when will the array become "good". Let's assume we get the array $$$b$$$ after one operation on array $$$a$$$, we get $$$b_i<b_{i+1}<b_{i+2}$$$. We can infer that $$$b_i=a_i,b_{i+1}=a_{i+1}$$$ and there is at least $$$a_j=a_{i+1}(j \le i)$$$, which shows that $$$a$$$ is not non-decreasing. In other words, after two operations, we can always get a "good" array. Then the calculating is trival.

Time complexity: $$$O(n)$$$.

#include <bits/stdc++.h>
using namespace std;
#define m_p make_pair
#define all(x) (x).begin(),(x).end()
#define sz(x) ((int)(x).size())
#define fi first
#define se second
typedef long long ll;
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
mt19937 rnf(2106);
const int N = 200005;

int n;
int a[N];

bool c[N];
void doit()
{
    for (int i = 1; i <= n; ++i)
        c[i] = false;
    int maxu = 0;
    for (int i = 1; i <= n; ++i)
    {
        if (c[a[i]])
            maxu = max(maxu, a[i]);
        c[a[i]] = true;
        a[i] = maxu;
    }
}

void solv()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];

    ll ans = 0;
    for (int i = 1; i <= n; ++i)
        ans += a[i];
    doit();
    for (int i = 1; i <= n; ++i)
        ans += a[i];
    doit();

    for (int i = 1; i <= n; ++i)
        ans += (n - i + 1) * 1LL * a[i];
    cout << ans << "\n";
}

int main()
{
    #ifdef SOMETHING
    freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    #endif // SOMETHING
    ios_base::sync_with_stdio(false), cin.tie(0);

    int tt = 1;
    cin >> tt;
    while (tt--)
    {
        solv();
    }
    return 0;
}

The title "Mad MAD Sum" is not only a pun on the words Mad and MAD (Maximum Appearing Duplicate), but also implies the solution to the problem :)

Obviously, when $$$a_i$$$ is large enough, we will definitely use operation $$$2$$$ on the $$$i$$$-th line. What is its specific value?

It is $$$5$$$(try to prove it). Now we can only consider $$$a_i \le 4$$$ cases.

From left to right, consider a greedy solution or a DP solution.

We observe that, in fact, only the $$$>$$$ to the left of $$$p$$$ and the $$$<$$$ to the right of $$$p$$$ change the direction of the pinball placed at position $$$p$$$ initially.

For convenience, let's assume $$$s_p$$$ is $$$>$$$, $$$k=min(countright(1,p),countleft(p+1,n))$$$, and the pinball leaves from the left boundary(for other situations, we can handle them in a similar way).

We can obtain $$$right[1,\ldots,k]$$$ and $$$left[1,\ldots,k]$$$ through prefix sum + binary search, where $$$right$$$ represents the indices of $$$>$$$ to the left of $$$p$$$ (in decreasing order), and $$$left$$$ represents the indices of $$$<$$$ to the right of $$$p$$$ (in increasing order).

We use $$$right$$$ and $$$left$$$ to describe the trace of the pinball:

The first segment: the pinball moves from $$$right_1$$$ to $$$left_1$$$;

The second segment: the pinball moves from $$$left_1$$$ to $$$right_2$$$;

The third segment: the pinball moves from $$$right_2$$$ to $$$left_3$$$;

$$$\ldots$$$

The $$$2k$$$-th segment: the pinball moves from $$$left_k$$$ to the left boundary.

It is not difficult to observe that we can use prefix sum to store the sum of indices, and then quickly calculate the time when the pinball moves.

#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef double db; 
typedef long long ll;
typedef unsigned long long ull;
const int N=1000010;
const int LOGN=28;
const ll  TMD=0;
const ll  INF=2147483647;
int  T,n;
ll   Sl[N],Sr[N],IDl[N],IDr[N];
char s[N];

int findpre(int x)
{
	int L=0,R=n+1,M;
	while(L+1!=R)
	{
		M=(L+R)>>1;
		if(Sr[M]<x) L=M;
		else R=M; 
	}
	return R;
}

int findsuf(int x)
{
	int L=0,R=n+1,M;
	while(L+1!=R)
	{
		M=(L+R)>>1;
		if(Sl[n]-Sl[M-1]<x) R=M;
		else L=M; 
	}
	return L;
}

int main()
{
	scanf("%d",&T);
	while(T--)
	{
    	        scanf("%d%s",&n,s);
		for(int i=1;i<=n;i++) 
		{
	  	  Sr[i]=Sr[i-1]+(s[i-1]=='>');
	  	  Sl[i]=Sl[i-1]+(s[i-1]=='<');
 		  IDr[i]=IDr[i-1]+i*(s[i-1]=='>'); 	
 		  IDl[i]=IDl[i-1]+i*(s[i-1]=='<'); 	
		}		
		for(int i=1;i<=n;i++)
		{
			if(s[i-1]=='>')
			{
				if(Sr[i]>Sl[n]-Sl[i])
				{
					int p=findpre(Sr[i]-(Sl[n]-Sl[i]));
					printf("%I64d ",2*((IDl[n]-IDl[i])-(IDr[i]-IDr[p-1]))+i+(n+1));
				}
				else
				{
					int p=findsuf((Sl[n]-Sl[i])-Sr[i]+1);
					printf("%I64d ",2*((IDl[p]-IDl[i])-(IDr[i]-IDr[0]))+i);
				}
			}
			else
			{
				if(Sr[i]>=Sl[n]-Sl[i-1])
				{
					int p=findpre(Sr[i]-(Sl[n]-Sl[i-1])+1);
					printf("%I64d ",2*((IDl[n]-IDl[i-1])-(IDr[i]-IDr[p-1]))-i+(n+1));
				}
				else
				{
					int p=findsuf((Sl[n]-Sl[i-1])-Sr[i]);
					printf("%I64d ",2*((IDl[p]-IDl[i-1])-(IDr[i]-IDr[0]))-i);
				}
			}
		}
		printf("\n");
	}
	
	return 0;
}

In fact, you don't need to hire the same Pokemon more than once.

Consider graph building.

How to reduce the number of edges in the graph?

Let's consider $$$n$$$ Pokémon as nodes, and defeating Pokémon $$$u$$$ by Pokémon $$$v$$$ as the edge $$$u \rightarrow v$$$. Then the problem is essentially finding the shortest path from $$$n$$$ to $$$1$$$.

If we brute force to construct the graph, the time complexity will be $$$O(n^2m)$$$, which is unacceptable. How can we find a better way to build the graph?

Recalling, we need to represent all processes like "Pokémon $$$u$$$ increased attribute $$$x$$$ by some value and defeated Pokémon $$$v$$$" using paths in the graph.

We will use the following graph building to achieve this. Overall, we consider each attribute separately. For the $$$x$$$-th attribute, we construct $$$2n$$$ virtual nodes $$$X_1,...,X_n$$$ and $$$Y_1,...,Y_n$$$, and connect each Pokémon based on the $$$x$$$-th attribute.

For example, $$$n=3$$$ and $$$a_{1,1}=9, a_{2,1}=6, a_{3,1}=1$$$, we have the following graph building for attribute $$$1$$$:

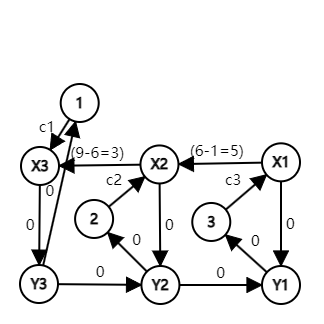
In this graph,for example,"Pokémon $$$3$$$ increased attribute $$$1$$$ by $$$8$$$ and defeated Pokémon $$$1$$$" can be represented as path $$$3 \rightarrow X1 \rightarrow X2 \rightarrow X3 \rightarrow Y3 \rightarrow 1$$$.

More generally, our graph building method is :

• Consider each attribute separately. Assuming we are processing the $$$i$$$-th attribute, insert all $$$a_{1,i} , \ldots ,a_{n,i}$$$ into $$$val$$$ and sort it (for convenience, we assume that they are pairwise different).

• Construct $$$2n$$$ virtual nodes $$$X_1,...,X_n$$$ and $$$Y_1,...,Y_n$$$;

• Add edge $$$X_i \rightarrow X_{i+1}$$$ with a value of $$$(val_{i+1}-val_i)$$$ for $$$1 \le i < n$$$;

• Add edge $$$Y_{i+1} \rightarrow Y_{i}$$$ with a value of $$$0$$$ for $$$1 \le i < n$$$;

• Add edge $$$X_i \rightarrow Y_{i}$$$ with a value of $$$0$$$ for $$$1 \le i \le n$$$;

• Add edge $$$i \rightarrow X_{rank_i}$$$ with a value of $$$c_i$$$ for $$$1 \le i \le n$$$;

• Add edge $$$Y_{rank_i} \rightarrow i$$$ with a value of $$$0$$$ for $$$1 \le i \le n$$$.

Then we just run Dijkstra algorithm in this graph. The time complexity is $$$O(nmlog(nm))$$$.

#include <bits/stdc++.h>
#define int long long
#define fi first
#define se second

using namespace std;

const int INFF = 1e18;

int32_t main()
{
        ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        
        int t;
        cin >> t;

        while (t --> 0) {
                int n, m;
                cin >> n >> m;

                vector<int> c(n + 1);
                for (int i = 1; i <= n; i++) cin >> c[i];

                vector<vector<int>> a(n + 1, vector<int>(m + 1));
                vector<vector<pair<int, int>>> b(m + 1);
                for (int i = 1; i <= n; i++) {
                        for (int j = 1; j <= m; j++) {
                                cin >> a[i][j];

                                b[j].push_back({a[i][j], i});
                        }
                }

                vector<vector<int>> rank(n + 1, vector<int>(m + 1));
                vector<vector<int>> dec(n + 1, vector<int>(m + 1));
                for (int j = 1; j <= m; j++) {
                        sort(b[j].begin(), b[j].end());

                        for (int i = 0; i < n; i++) {
                                auto [x, id] = b[j][i];
                                rank[id][j] = i + 1;
                                dec[i + 1][j] = id;
                        }
                }

                int ans = INFF;
                vector<int> vis(n + 1, 0);
                vector<vector<int>> dist(n + 1, vector<int>(m + 1, INFF));
                priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> pq;
                vis[1] = 1;
                for (int j = 1; j <= m; j++) dist[1][j] = 0, pq.push({dist[1][j], 1, j});
                while (!pq.empty()) {
                        auto [w, x, t] = pq.top();
                        pq.pop();

                        if (dist[x][t] < w) continue;

                        if (x == n) ans = min(ans, w + c[n]);

                        if (rank[x][t] < n) {
                                int z = dec[rank[x][t] + 1][t];
                                if (w < dist[z][t]) {
                                        dist[z][t] = w;
                                        pq.push({dist[z][t], z, t});
                                }
                        }

                        if (rank[x][t] > 1) {
                                int z = dec[rank[x][t] - 1][t];
                                if (w + a[x][t] - a[z][t] < dist[z][t]) {
                                        dist[z][t] = w + a[x][t] - a[z][t];
                                        pq.push({dist[z][t], z, t});
                                }
                        }

                        if (!vis[x]) {
                                vis[x] = 1;
                                for (int j = 1; j <= m; j++) {
                                        if (w + c[x] < dist[x][j]) {
                                                dist[x][j] = w + c[x];
                                                pq.push({dist[x][j], x, j});
                                        }
                                }
                        }
                }

                cout << ans << '\n';
        }
        
        return 0;
}

First we use the line segment tree to maintain sequence $$$b$$$. For the nodes $$$[l,r]$$$ on each line segment tree, we maintain the first and last occurrence positions of each binary bit in the interval.

We need to merge the two intervals, whether it is modification or query. Suppose you want to use the information of $$$[l, mid], [mid +1, r]$$$ to merge the information of $$$[l, r]$$$. Consider the answer that spans two intervals. If we want to make the $$$i$$$-th position of the interval OR $$$1$$$, then there are two possibilities

1. Select the last occurrence position $$$P$$$ of the $$$i$$$-th bit in $$$[l,mid].$$$

2. Select the first occurrence position $$$Q$$$ of the $$$i$$$-th bit in $$$[mid+1,r].$$$

Let $$$x = max(a[P], a[P+1],\ldots, a[mid]), y = max(a[mid + 1], a[mid + 2], \ldots, a[Q]).$$$

If $$$x<=y,$$$ we can choose the position $$$P$$$ greedily, because his price is smaller. If you choose $$$Q,$$$ then you must also choose $$$P,$$$ because choosing $$$P$$$ does not increase max $$$a.$$$ Otherwise, select $$$Q$$$ on the contrary.

With the above greedy, then you can enumerate the first binary bit $$$i$$$ that is larger than $$$v$$$. The $$$i$$$-th bit of the interval OR must be $$$1$$$, and the $$$i$$$-th bit of $$$v$$$ is $$$0$$$. For the $$$j$$$-th $$$(j >i)$$$ bit, if the $$$j$$$-th bit of $$$v$$$ is $$$1$$$, then the $$$j$$$-th bit must also be $$$1$$$. The rest of the bits can be regarded as $$$0$$$ or $$$1$$$, you only need to deal with these bits that must be selected $$$1$$$ greedily, and expand the interval.

You can use the st table $$$O(1)$$$ to find the interval max of $$$a$$$, so you can merge the information of the two intervals in the time of $$$O(log V)$$$. With the line segment tree, $$$O(q log n log V + n log V)$$$ can be done.

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 5e5 + 10, V = 30, inf = INT_MAX, L = 18;
int n, q, S, a[N], b[N];
struct Rmq
{
   int st[L][N];
   void init()
   {
      for (int i = 1; i <= n; i++)
         st[0][i] = a[i];
      for (int i = 1; i < L; i++)
      {
         for (int j = 1; j <= n - (1 << i) + 1; j++)
         {
            st[i][j] = max(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
         }
      }
   }
   int qry(int l, int r)
   {
      int k = __lg(r - l + 1);
      return max(st[k][l], st[k][r - (1 << k) + 1]);
   }
} ds;
struct Info
{
   int pre[V], suf[V];
   int ans, l, r;
   Info()
   {
      memset(pre, 0, sizeof(pre));
      memset(suf, 0, sizeof(suf));
      ans = inf, l = r = 0;
   }
   Info(const Info &x, const Info &y)
   {
      for (int i = 0; i < V; i++)
      {
         pre[i] = x.pre[i] ? x.pre[i] : y.pre[i];
         suf[i] = y.suf[i] ? y.suf[i] : x.suf[i];
      }
      ans = inf, l = r = 0;
   }
   friend Info operator+(const Info &x, const Info &y)
   {
      Info z(x, y);
      z.ans = min(x.ans, y.ans), z.l = x.l, z.r = y.r;
      int pl = x.r, pr = y.l;
      if (!pl)
         return z;
      for (int i = V - 1; i >= 0; i--)
      {
         int u = x.suf[i], v = y.pre[i];
         if (u)
            u = min(u, pl);
         if (v)
            v = max(v, pr);
         int lans = u ? ds.qry(u, pr) : inf;
         int rans = v ? ds.qry(pl, v) : inf;
         if (lans < rans)
         {
            if (S >> i & 1)
            {
               if (lans < z.ans)
                  pl = u;
               else
                  break;
            }
            else
               z.ans = min(z.ans, lans);
         }
         else
         {
            if (S >> i & 1)
            {
               if (rans < z.ans)
                  pr = v;
               else
                  break;
            }
            else
               z.ans = min(z.ans, rans);
         }
      }
      return z;
   }
   void clear()
   {
      *this = Info();
   }
   void upd(int p)
   {
      l = r = p, ans = b[p] > S ? a[p] : inf;
      memset(pre, 0, sizeof(pre));
      memset(suf, 0, sizeof(suf));
      for (int j = 0; j < V; j++)
      {
         if (b[p] >> j & 1)
         {
            suf[j] = p;
            pre[j] = p;
         }
      }
   }
} ans;
void reply(const Info &cur)
{
   ans = ans + cur;
}
struct Node
{
   Node *ls, *rs;
   int l, r, mid;
   Info info;
   void up()
   {
      info = ls->info + rs->info;
   }
   void update(int p)
   {
      if (l == r)
         return info.upd(l);
      p <= mid ? ls->update(p) : rs->update(p);
      up();
   }
   void query(int ql, int qr)
   {
      if (l >= ql && r <= qr)
         return reply(info);
      if (ql <= mid)
         ls->query(ql, qr);
      if (qr > mid)
         rs->query(ql, qr);
   }
} mempool[N + 5 << 1], *cnt = mempool, *rt;
Node *build(int l, int r)
{
   Node *u = cnt++;
   int mid = l + r >> 1;
   u->l = l, u->r = r, u->mid = mid;
   if (l == r)
   {
      u->info.upd(l);
      return u;
   }
   u->ls = build(l, mid);
   u->rs = build(mid + 1, r);
   u->up();
   return u;
}
 
void solve()
{
   cin >> n >> S;
   S--;
   for (int i = 1; i <= n; i++)
      cin >> a[i];
   ds.init();
   for (int i = 1; i <= n; i++)
      cin >> b[i];
   rt = build(1, n);
   cin >> q;
   for (int i = 0; i < q; i++)
   {
      int opt;
      cin >> opt;
      if (opt == 1)
      {
         int p, x;
         cin >> p >> x;
         b[p] = x;
         rt->update(p);
      }
      else
      {
         int l, r;
         cin >> l >> r;
         ans.clear();
         rt->query(l, r);
         cout << (ans.ans == inf ? -1 : ans.ans) << ' ';
      }
   }
   cout << "\n";
}
int main()
{
#ifndef ONLINE_JUDGE
   freopen("input.txt", "r", stdin);
   freopen("output.txt", "w", stdout);
#endif
   ios_base::sync_with_stdio(0);
   cin.tie(0);
   cout.tie(0);
   ios::sync_with_stdio(false), cin.tie(0);
   int t = 0;
   cin >> t;
   while (t--)
   {
      solve();
   }
 
   // 	cerr << 1.0 * clock() / CLOCKS_PER_SEC << '\n';
   return 0;
}

We found it difficult to directly calculate all valid permutations. How about calculating all invalid permutations?

Can you come up with an $$$O(n^2)$$$ DP solution?

How to optimize the $$$O(n^2)$$$ DP solution?

We found it difficult to directly calculate all valid permutations. Consider calculating all invalid permutations and subtract it from $$$n!$$$.

Let's first make some notes. We note $$$P_i=max(p_1,...,p_i),Q_i=max(q_1,...,q_i)$$$,and $$$last_i=max(j)(P_j \neq P_i)$$$.And note the values of all extreme points is $$$val[1,...,m]$$$ and positions is $$$pos[1,...,m]$$$.

For example,$$$p=[3,1,4,2,6,5]$$$,we get $$$m=3$$$, $$$val=[3,4,6]$$$ and $$$pos=[1,3,5]$$$.

Let’s call a permutation $$$q$$$ “i-invalid” if there’s an index $$$j$$$ satisfying $$$Q_j=P_j=val_i$$$.

Note $$$S_i$$$ as the set of all “i-invalid” permutations.According to the Inclusion-Exclusion Principle,the answer is $$$n!-(|S_1|+|S_2|+...)+(|S_1∩S_2|+|S_1∩S_3|+...)-...$$$

Consider put $$$val_i$$$ in $$$q$$$ to make $$$q$$$ “i-invalid”.There’re $$$2$$$ kinds of ways:

• $$$q_j=val_i(1 \le j < pos_i)$$$ and $$$Q_{pos_i}=val_i$$$;

• $$$q_j=val_i(pos_i \le j< pos_{i+1})$$$ and $$$Q_{pos_i}=val_i$$$.

In both cases,we call the first $$$max(j,pos_i)$$$ numbers are “determined”. In other words,they’re some numbers in $$$[1,val_i]$$$.

Then we can find an $$$O(n^2)$$$ DP. Note $$$dp_{i,j}$$$ — $$$i$$$ stands for the first $$$i$$$ numbers is “determined”,and $$$j$$$ stands for $$$j$$$ extreme values are “invalid”. In fact we only care about the parity of $$$j$$$,so $$$j=0,1$$$. Note for the first $$$i$$$ numbers are “determined” automatically means $$$Q_i=P_i$$$. In addition,$$$q_i=P_i(P_i=P_{i-1})$$$ or $$$q_i<P_i(P_i \neq P_{i-1})$$$.

We get a DP formula $$$dp_{i,j}= \Sigma_{k=0}^{last_i} dp_{k,j \oplus 1} \cdot A^{P_i-k-1}_{i-k-1} \cdot (P_i==P_{i+1}?1:i-k)$$$

Here is a small trick to reduce the constant. If we note $$$f_i=dp_{i,0}-dp_{i,1}$$$, we get a more concise formula $$$f_{i}= -\Sigma_{j=0}^{last_i} f_{j} \cdot A^{P_i-j-1}_{i-j-1} \cdot (P_i==P_{i+1}?1:i-j)$$$

We perform the following transformation on the formula.

① For $$$i$$$ satisfying $$$P_i=P_{i-1}$$$, we get

$$$f_{i}= -\Sigma_{j=0}^{last_i} f_{j} \cdot A^{P_i-j-1}_{i-j-1} = -[(P_i-i)!]^{-1} \Sigma_{j=0}^{last_i} f_{j} \cdot (P_i-j-1)!$$$

② For $$$i$$$ satisfying $$$P_i \neq P_{i-1}$$$, we get

$$$f_{i}= -\Sigma_{j=0}^{last_i} f_{j} \cdot A^{P_i-j-1}_{i-j-1} \cdot (i-j) = -i[(P_i-i)!]^{-1} \Sigma_{j=0}^{last_i} f_{j} \cdot (P_i-j-1)! + [(P_i-i)!]^{-1} \Sigma_{j=0}^{last_i} jf_{j} \cdot (P_i-j-1)!$$$

After that, we have transformed the formula into a classical form $$$f(i)= h(i) \Sigma_{j=0}^{i-1} f(j) \cdot g(i-j)$$$, which can be calculate in $$$O(n log^2 n)$$$ by D&C+FFT.

#include<bits/stdc++.h>
using namespace std;

#define all(a) a.begin(),a.end()
#define pb push_back
#define sz(a) ((int)a.size())

using ll=long long;
using u32=unsigned int;
using u64=unsigned long long;
using i128=__int128;
using u128=unsigned __int128;
using f128=__float128;

using pii=pair<int,int>;
using pll=pair<ll,ll>;

template<typename T> using vc=vector<T>;
template<typename T> using vvc=vc<vc<T>>;
template<typename T> using vvvc=vc<vvc<T>>;

using vi=vc<int>;
using vll=vc<ll>;
using vvi=vc<vi>;
using vvll=vc<vll>;

#define vv(type,name,n,...) \
    vector<vector<type>> name(n,vector<type>(__VA_ARGS__))
#define vvv(type,name,n,m,...) \
    vector<vector<vector<type>>> name(n,vector<vector<type>>(m,vector<type>(__VA_ARGS__)))

template<typename T> using min_heap=priority_queue<T,vector<T>,greater<T>>;
template<typename T> using max_heap=priority_queue<T>;

// https://trap.jp/post/1224/
#define rep1(n) for(ll i=0; i<(ll)(n); ++i)
#define rep2(i,n) for(ll i=0; i<(ll)(n); ++i)
#define rep3(i,a,b) for(ll i=(ll)(a); i<(ll)(b); ++i)
#define rep4(i,a,b,c) for(ll i=(ll)(a); i<(ll)(b); i+=(c))
#define cut4(a,b,c,d,e,...) e
#define rep(...) cut4(__VA_ARGS__,rep4,rep3,rep2,rep1)(__VA_ARGS__)
#define per1(n) for(ll i=((ll)n)-1; i>=0; --i)
#define per2(i,n) for(ll i=((ll)n)-1; i>=0; --i)
#define per3(i,a,b) for(ll i=((ll)a)-1; i>=(ll)(b); --i)
#define per4(i,a,b,c) for(ll i=((ll)a)-1; i>=(ll)(b); i-=(c))
#define per(...) cut4(__VA_ARGS__,per4,per3,per2,per1)(__VA_ARGS__)
#define rep_subset(i,s) for(ll i=(s); i>=0; i=(i==0?-1:(i-1)&(s)))

template<typename T, typename S> constexpr T ifloor(const T a, const S b){return a/b-(a%b&&(a^b)<0);}
template<typename T, typename S> constexpr T iceil(const T a, const S b){return ifloor(a+b-1,b);}

template<typename T>
void sort_unique(vector<T> &vec){
    sort(vec.begin(),vec.end());
    vec.resize(unique(vec.begin(),vec.end())-vec.begin());
}

template<typename T, typename S> constexpr bool chmin(T &a, const S b){if(a>b) return a=b,true; return false;}
template<typename T, typename S> constexpr bool chmax(T &a, const S b){if(a<b) return a=b,true; return false;}

template<typename T, typename S> istream& operator >> (istream& i, pair<T,S> &p){return i >> p.first >> p.second;}
template<typename T, typename S> ostream& operator << (ostream& o, const pair<T,S> &p){return o << p.first << ' ' << p.second;}

#ifdef i_am_noob
#define bug(...) cerr << "#" << __LINE__ << ' ' << #__VA_ARGS__ << "- ", _do(__VA_ARGS__)
template<typename T> void _do(vector<T> x){for(auto i: x) cerr << i << ' ';cerr << "\n";}
template<typename T> void _do(set<T> x){for(auto i: x) cerr << i << ' ';cerr << "\n";}
template<typename T> void _do(unordered_set<T> x){for(auto i: x) cerr << i << ' ';cerr << "\n";}
template<typename T> void _do(T && x) {cerr << x << endl;}
template<typename T, typename ...S> void _do(T && x, S&&...y) {cerr << x << ", "; _do(y...);}
#else
#define bug(...) 777771449
#endif

template<typename T> void print(vector<T> x){for(auto i: x) cout << i << ' ';cout << "\n";}
template<typename T> void print(set<T> x){for(auto i: x) cout << i << ' ';cout << "\n";}
template<typename T> void print(unordered_set<T> x){for(auto i: x) cout << i << ' ';cout << "\n";}
template<typename T> void print(T && x) {cout << x << "\n";}
template<typename T, typename... S> void print(T && x, S&&... y) {cout << x << ' ';print(y...);}

template<typename T> istream& operator >> (istream& i, vector<T> &vec){for(auto &x: vec) i >> x; return i;}

vvi read_graph(int n, int m, int base=1){
    vvi adj(n);
    for(int i=0,u,v; i<m; ++i){
        cin >> u >> v,u-=base,v-=base;
        adj[u].pb(v),adj[v].pb(u);
    }
    return adj;
}

vvi read_tree(int n, int base=1){return read_graph(n,n-1,base);}

template<typename T, typename S> pair<T,S> operator + (const pair<T,S> &a, const pair<T,S> &b){return {a.first+b.first,a.second+b.second};}

template<typename T> constexpr T inf=0;
template<> constexpr int inf<int> = 0x3f3f3f3f;
template<> constexpr ll inf<ll> = 0x3f3f3f3f3f3f3f3f;

template<typename T> vector<T> operator += (vector<T> &a, int val){for(auto &i: a) i+=val; return a;}

template<typename T> T isqrt(const T &x){T y=sqrt(x+2); while(y*y>x) y--; return y;}

#define ykh mt19937 rng(chrono::steady_clock::now().time_since_epoch().count())



#include <utility>

namespace atcoder {

namespace internal {

// @param m `1 <= m`
// @return x mod m
constexpr long long safe_mod(long long x, long long m) {
    x %= m;
    if (x < 0) x += m;
    return x;
}

// Fast modular multiplication by barrett reduction
// Reference: https://en.wikipedia.org/wiki/Barrett_reduction
// NOTE: reconsider after Ice Lake
struct barrett {
    unsigned int _m;
    unsigned long long im;

    // @param m `1 <= m < 2^31`
    barrett(unsigned int m) : _m(m), im((unsigned long long)(-1) / m + 1) {}

    // @return m
    unsigned int umod() const { return _m; }

    // @param a `0 <= a < m`
    // @param b `0 <= b < m`
    // @return `a * b % m`
    unsigned int mul(unsigned int a, unsigned int b) const {
        // [1] m = 1
        // a = b = im = 0, so okay

        // [2] m >= 2
        // im = ceil(2^64 / m)
        // -> im * m = 2^64 + r (0 <= r < m)
        // let z = a*b = c*m + d (0 <= c, d < m)
        // a*b * im = (c*m + d) * im = c*(im*m) + d*im = c*2^64 + c*r + d*im
        // c*r + d*im < m * m + m * im < m * m + 2^64 + m <= 2^64 + m * (m + 1) < 2^64 * 2
        // ((ab * im) >> 64) == c or c + 1
        unsigned long long z = a;
        z *= b;
#ifdef _MSC_VER
        unsigned long long x;
        _umul128(z, im, &x);
#else
        unsigned long long x =
            (unsigned long long)(((unsigned __int128)(z)*im) >> 64);
#endif
        unsigned int v = (unsigned int)(z - x * _m);
        if (_m <= v) v += _m;
        return v;
    }
};

// @param n `0 <= n`
// @param m `1 <= m`
// @return `(x ** n) % m`
constexpr long long pow_mod_constexpr(long long x, long long n, int m) {
    if (m == 1) return 0;
    unsigned int _m = (unsigned int)(m);
    unsigned long long r = 1;
    unsigned long long y = safe_mod(x, m);
    while (n) {
        if (n & 1) r = (r * y) % _m;
        y = (y * y) % _m;
        n >>= 1;
    }
    return r;
}

// Reference:
// M. Forisek and J. Jancina,
// Fast Primality Testing for Integers That Fit into a Machine Word
// @param n `0 <= n`
constexpr bool is_prime_constexpr(int n) {
    if (n <= 1) return false;
    if (n == 2 || n == 7 || n == 61) return true;
    if (n % 2 == 0) return false;
    long long d = n - 1;
    while (d % 2 == 0) d /= 2;
    constexpr long long bases[3] = {2, 7, 61};
    for (long long a : bases) {
        long long t = d;
        long long y = pow_mod_constexpr(a, t, n);
        while (t != n - 1 && y != 1 && y != n - 1) {
            y = y * y % n;
            t <<= 1;
        }
        if (y != n - 1 && t % 2 == 0) {
            return false;
        }
    }
    return true;
}
template <int n> constexpr bool is_prime = is_prime_constexpr(n);

// @param b `1 <= b`
// @return pair(g, x) s.t. g = gcd(a, b), xa = g (mod b), 0 <= x < b/g
constexpr std::pair<long long, long long> inv_gcd(long long a, long long b) {
    a = safe_mod(a, b);
    if (a == 0) return {b, 0};

    // Contracts:
    // [1] s - m0 * a = 0 (mod b)
    // [2] t - m1 * a = 0 (mod b)
    // [3] s * |m1| + t * |m0| <= b
    long long s = b, t = a;
    long long m0 = 0, m1 = 1;

    while (t) {
        long long u = s / t;
        s -= t * u;
        m0 -= m1 * u;  // |m1 * u| <= |m1| * s <= b

        // [3]:
        // (s - t * u) * |m1| + t * |m0 - m1 * u|
        // <= s * |m1| - t * u * |m1| + t * (|m0| + |m1| * u)
        // = s * |m1| + t * |m0| <= b

        auto tmp = s;
        s = t;
        t = tmp;
        tmp = m0;
        m0 = m1;
        m1 = tmp;
    }
    // by [3]: |m0| <= b/g
    // by g != b: |m0| < b/g
    if (m0 < 0) m0 += b / s;
    return {s, m0};
}

// Compile time primitive root
// @param m must be prime
// @return primitive root (and minimum in now)
constexpr int primitive_root_constexpr(int m) {
    if (m == 2) return 1;
    if (m == 167772161) return 3;
    if (m == 469762049) return 3;
    if (m == 754974721) return 11;
    if (m == 998244353) return 3;
    int divs[20] = {};
    divs[0] = 2;
    int cnt = 1;
    int x = (m - 1) / 2;
    while (x % 2 == 0) x /= 2;
    for (int i = 3; (long long)(i)*i <= x; i += 2) {
        if (x % i == 0) {
            divs[cnt++] = i;
            while (x % i == 0) {
                x /= i;
            }
        }
    }
    if (x > 1) {
        divs[cnt++] = x;
    }
    for (int g = 2;; g++) {
        bool ok = true;
        for (int i = 0; i < cnt; i++) {
            if (pow_mod_constexpr(g, (m - 1) / divs[i], m) == 1) {
                ok = false;
                break;
            }
        }
        if (ok) return g;
    }
}
template <int m> constexpr int primitive_root = primitive_root_constexpr(m);

}  // namespace internal

}  // namespace atcoder


#include <cassert>
#include <numeric>
#include <type_traits>

namespace atcoder {

namespace internal {

#ifndef _MSC_VER
template <class T>
using is_signed_int128 =
    typename std::conditional<std::is_same<T, __int128_t>::value ||
                                  std::is_same<T, __int128>::value,
                              std::true_type,
                              std::false_type>::type;

template <class T>
using is_unsigned_int128 =
    typename std::conditional<std::is_same<T, __uint128_t>::value ||
                                  std::is_same<T, unsigned __int128>::value,
                              std::true_type,
                              std::false_type>::type;

template <class T>
using make_unsigned_int128 =
    typename std::conditional<std::is_same<T, __int128_t>::value,
                              __uint128_t,
                              unsigned __int128>;

template <class T>
using is_integral = typename std::conditional<std::is_integral<T>::value ||
                                                  is_signed_int128<T>::value ||
                                                  is_unsigned_int128<T>::value,
                                              std::true_type,
                                              std::false_type>::type;

template <class T>
using is_signed_int = typename std::conditional<(is_integral<T>::value &&
                                                 std::is_signed<T>::value) ||
                                                    is_signed_int128<T>::value,
                                                std::true_type,
                                                std::false_type>::type;

template <class T>
using is_unsigned_int =
    typename std::conditional<(is_integral<T>::value &&
                               std::is_unsigned<T>::value) ||
                                  is_unsigned_int128<T>::value,
                              std::true_type,
                              std::false_type>::type;

template <class T>
using to_unsigned = typename std::conditional<
    is_signed_int128<T>::value,
    make_unsigned_int128<T>,
    typename std::conditional<std::is_signed<T>::value,
                              std::make_unsigned<T>,
                              std::common_type<T>>::type>::type;

#else

template <class T> using is_integral = typename std::is_integral<T>;

template <class T>
using is_signed_int =
    typename std::conditional<is_integral<T>::value && std::is_signed<T>::value,
                              std::true_type,
                              std::false_type>::type;

template <class T>
using is_unsigned_int =
    typename std::conditional<is_integral<T>::value &&
                                  std::is_unsigned<T>::value,
                              std::true_type,
                              std::false_type>::type;

template <class T>
using to_unsigned = typename std::conditional<is_signed_int<T>::value,
                                              std::make_unsigned<T>,
                                              std::common_type<T>>::type;

#endif

template <class T>
using is_signed_int_t = std::enable_if_t<is_signed_int<T>::value>;

template <class T>
using is_unsigned_int_t = std::enable_if_t<is_unsigned_int<T>::value>;

template <class T> using to_unsigned_t = typename to_unsigned<T>::type;

}  // namespace internal

}  // namespace atcoder

#include <cassert>
#include <numeric>
#include <type_traits>

#ifdef _MSC_VER
#include <intrin.h>
#endif

namespace atcoder {

namespace internal {

struct modint_base {};
struct static_modint_base : modint_base {};

template <class T> using is_modint = std::is_base_of<modint_base, T>;
template <class T> using is_modint_t = std::enable_if_t<is_modint<T>::value>;

}  // namespace internal

template <int m, std::enable_if_t<(1 <= m)>* = nullptr>
struct static_modint : internal::static_modint_base {
    using mint = static_modint;

  public:
    static constexpr int mod() { return m; }
    static mint raw(int v) {
        mint x;
        x._v = v;
        return x;
    }

    static_modint() : _v(0) {}
    template <class T, internal::is_signed_int_t<T>* = nullptr>
    static_modint(T v) {
        long long x = (long long)(v % (long long)(umod()));
        if (x < 0) x += umod();
        _v = (unsigned int)(x);
    }
    template <class T, internal::is_unsigned_int_t<T>* = nullptr>
    static_modint(T v) {
        _v = (unsigned int)(v % umod());
    }
    static_modint(bool v) { _v = ((unsigned int)(v) % umod()); }

    unsigned int val() const { return _v; }

    mint& operator++() {
        _v++;
        if (_v == umod()) _v = 0;
        return *this;
    }
    mint& operator--() {
        if (_v == 0) _v = umod();
        _v--;
        return *this;
    }
    mint operator++(int) {
        mint result = *this;
        ++*this;
        return result;
    }
    mint operator--(int) {
        mint result = *this;
        --*this;
        return result;
    }

    mint& operator+=(const mint& rhs) {
        _v += rhs._v;
        if (_v >= umod()) _v -= umod();
        return *this;
    }
    mint& operator-=(const mint& rhs) {
        _v -= rhs._v;
        if (_v >= umod()) _v += umod();
        return *this;
    }
    mint& operator*=(const mint& rhs) {
        unsigned long long z = _v;
        z *= rhs._v;
        _v = (unsigned int)(z % umod());
        return *this;
    }
    mint& operator/=(const mint& rhs) { return *this = *this * rhs.inv(); }

    mint operator+() const { return *this; }
    mint operator-() const { return mint() - *this; }

    mint pow(long long n) const {
        assert(0 <= n);
        mint x = *this, r = 1;
        while (n) {
            if (n & 1) r *= x;
            x *= x;
            n >>= 1;
        }
        return r;
    }
    mint inv() const {
        if (prime) {
            assert(_v);
            return pow(umod() - 2);
        } else {
            auto eg = internal::inv_gcd(_v, m);
            assert(eg.first == 1);
            return eg.second;
        }
    }

    friend mint operator+(const mint& lhs, const mint& rhs) {
        return mint(lhs) += rhs;
    }
    friend mint operator-(const mint& lhs, const mint& rhs) {
        return mint(lhs) -= rhs;
    }
    friend mint operator*(const mint& lhs, const mint& rhs) {
        return mint(lhs) *= rhs;
    }
    friend mint operator/(const mint& lhs, const mint& rhs) {
        return mint(lhs) /= rhs;
    }
    friend bool operator==(const mint& lhs, const mint& rhs) {
        return lhs._v == rhs._v;
    }
    friend bool operator!=(const mint& lhs, const mint& rhs) {
        return lhs._v != rhs._v;
    }

  private:
    unsigned int _v;
    static constexpr unsigned int umod() { return m; }
    static constexpr bool prime = internal::is_prime<m>;
};

template <int id> struct dynamic_modint : internal::modint_base {
    using mint = dynamic_modint;

  public:
    static int mod() { return (int)(bt.umod()); }
    static void set_mod(int m) {
        assert(1 <= m);
        bt = internal::barrett(m);
    }
    static mint raw(int v) {
        mint x;
        x._v = v;
        return x;
    }

    dynamic_modint() : _v(0) {}
    template <class T, internal::is_signed_int_t<T>* = nullptr>
    dynamic_modint(T v) {
        long long x = (long long)(v % (long long)(mod()));
        if (x < 0) x += mod();
        _v = (unsigned int)(x);
    }
    template <class T, internal::is_unsigned_int_t<T>* = nullptr>
    dynamic_modint(T v) {
        _v = (unsigned int)(v % mod());
    }
    dynamic_modint(bool v) { _v = ((unsigned int)(v) % mod()); }

    unsigned int val() const { return _v; }

    mint& operator++() {
        _v++;
        if (_v == umod()) _v = 0;
        return *this;
    }
    mint& operator--() {
        if (_v == 0) _v = umod();
        _v--;
        return *this;
    }
    mint operator++(int) {
        mint result = *this;
        ++*this;
        return result;
    }
    mint operator--(int) {
        mint result = *this;
        --*this;
        return result;
    }

    mint& operator+=(const mint& rhs) {
        _v += rhs._v;
        if (_v >= umod()) _v -= umod();
        return *this;
    }
    mint& operator-=(const mint& rhs) {
        _v += mod() - rhs._v;
        if (_v >= umod()) _v -= umod();
        return *this;
    }
    mint& operator*=(const mint& rhs) {
        _v = bt.mul(_v, rhs._v);
        return *this;
    }
    mint& operator/=(const mint& rhs) { return *this = *this * rhs.inv(); }

    mint operator+() const { return *this; }
    mint operator-() const { return mint() - *this; }

    mint pow(long long n) const {
        assert(0 <= n);
        mint x = *this, r = 1;
        while (n) {
            if (n & 1) r *= x;
            x *= x;
            n >>= 1;
        }
        return r;
    }
    mint inv() const {
        auto eg = internal::inv_gcd(_v, mod());
        assert(eg.first == 1);
        return eg.second;
    }

    friend mint operator+(const mint& lhs, const mint& rhs) {
        return mint(lhs) += rhs;
    }
    friend mint operator-(const mint& lhs, const mint& rhs) {
        return mint(lhs) -= rhs;
    }
    friend mint operator*(const mint& lhs, const mint& rhs) {
        return mint(lhs) *= rhs;
    }
    friend mint operator/(const mint& lhs, const mint& rhs) {
        return mint(lhs) /= rhs;
    }
    friend bool operator==(const mint& lhs, const mint& rhs) {
        return lhs._v == rhs._v;
    }
    friend bool operator!=(const mint& lhs, const mint& rhs) {
        return lhs._v != rhs._v;
    }

  private:
    unsigned int _v;
    static internal::barrett bt;
    static unsigned int umod() { return bt.umod(); }
};
template <int id> internal::barrett dynamic_modint<id>::bt = 998244353;

using modint998244353 = static_modint<998244353>;
using modint1000000007 = static_modint<1000000007>;
using modint = dynamic_modint<-1>;

namespace internal {

template <class T>
using is_static_modint = std::is_base_of<internal::static_modint_base, T>;

template <class T>
using is_static_modint_t = std::enable_if_t<is_static_modint<T>::value>;

template <class> struct is_dynamic_modint : public std::false_type {};
template <int id>
struct is_dynamic_modint<dynamic_modint<id>> : public std::true_type {};

template <class T>
using is_dynamic_modint_t = std::enable_if_t<is_dynamic_modint<T>::value>;

}  // namespace internal

}  // namespace atcoder


#include <algorithm>
#include <array>

#ifdef _MSC_VER
#include <intrin.h>
#endif

namespace atcoder {

namespace internal {

// @param n `0 <= n`
// @return minimum non-negative `x` s.t. `n <= 2**x`
int ceil_pow2(int n) {
    int x = 0;
    while ((1U << x) < (unsigned int)(n)) x++;
    return x;
}

// @param n `1 <= n`
// @return minimum non-negative `x` s.t. `(n & (1 << x)) != 0`
int bsf(unsigned int n) {
#ifdef _MSC_VER
    unsigned long index;
    _BitScanForward(&index, n);
    return index;
#else
    return __builtin_ctz(n);
#endif
}

}  // namespace internal

}  // namespace atcoder

#include <cassert>
#include <type_traits>
#include <vector>

namespace atcoder {

namespace internal {

template <class mint, internal::is_static_modint_t<mint>* = nullptr>
void butterfly(std::vector<mint>& a) {
    static constexpr int g = internal::primitive_root<mint::mod()>;
    int n = int(a.size());
    int h = internal::ceil_pow2(n);

    static bool first = true;
    static mint sum_e[30];  // sum_e[i] = ies[0] * ... * ies[i - 1] * es[i]
    if (first) {
        first = false;
        mint es[30], ies[30];  // es[i]^(2^(2+i)) == 1
        int cnt2 = bsf(mint::mod() - 1);
        mint e = mint(g).pow((mint::mod() - 1) >> cnt2), ie = e.inv();
        for (int i = cnt2; i >= 2; i--) {
            // e^(2^i) == 1
            es[i - 2] = e;
            ies[i - 2] = ie;
            e *= e;
            ie *= ie;
        }
        mint now = 1;
        for (int i = 0; i <= cnt2 - 2; i++) {
            sum_e[i] = es[i] * now;
            now *= ies[i];
        }
    }
    for (int ph = 1; ph <= h; ph++) {
        int w = 1 << (ph - 1), p = 1 << (h - ph);
        mint now = 1;
        for (int s = 0; s < w; s++) {
            int offset = s << (h - ph + 1);
            for (int i = 0; i < p; i++) {
                auto l = a[i + offset];
                auto r = a[i + offset + p] * now;
                a[i + offset] = l + r;
                a[i + offset + p] = l - r;
            }
            now *= sum_e[bsf(~(unsigned int)(s))];
        }
    }
}

template <class mint, internal::is_static_modint_t<mint>* = nullptr>
void butterfly_inv(std::vector<mint>& a) {
    static constexpr int g = internal::primitive_root<mint::mod()>;
    int n = int(a.size());
    int h = internal::ceil_pow2(n);

    static bool first = true;
    static mint sum_ie[30];  // sum_ie[i] = es[0] * ... * es[i - 1] * ies[i]
    if (first) {
        first = false;
        mint es[30], ies[30];  // es[i]^(2^(2+i)) == 1
        int cnt2 = bsf(mint::mod() - 1);
        mint e = mint(g).pow((mint::mod() - 1) >> cnt2), ie = e.inv();
        for (int i = cnt2; i >= 2; i--) {
            // e^(2^i) == 1
            es[i - 2] = e;
            ies[i - 2] = ie;
            e *= e;
            ie *= ie;
        }
        mint now = 1;
        for (int i = 0; i <= cnt2 - 2; i++) {
            sum_ie[i] = ies[i] * now;
            now *= es[i];
        }
    }

    for (int ph = h; ph >= 1; ph--) {
        int w = 1 << (ph - 1), p = 1 << (h - ph);
        mint inow = 1;
        for (int s = 0; s < w; s++) {
            int offset = s << (h - ph + 1);
            for (int i = 0; i < p; i++) {
                auto l = a[i + offset];
                auto r = a[i + offset + p];
                a[i + offset] = l + r;
                a[i + offset + p] =
                    (unsigned long long)(mint::mod() + l.val() - r.val()) *
                    inow.val();
            }
            inow *= sum_ie[bsf(~(unsigned int)(s))];
        }
    }
}

}  // namespace internal

template <class mint, internal::is_static_modint_t<mint>* = nullptr>
std::vector<mint> convolution(std::vector<mint> a, std::vector<mint> b) {
    int n = int(a.size()), m = int(b.size());
    if (!n || !m) return {};
    if (std::min(n, m) <= 60) {
        if (n < m) {
            std::swap(n, m);
            std::swap(a, b);
        }
        std::vector<mint> ans(n + m - 1);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                ans[i + j] += a[i] * b[j];
            }
        }
        return ans;
    }
    int z = 1 << internal::ceil_pow2(n + m - 1);
    a.resize(z);
    internal::butterfly(a);
    b.resize(z);
    internal::butterfly(b);
    for (int i = 0; i < z; i++) {
        a[i] *= b[i];
    }
    internal::butterfly_inv(a);
    a.resize(n + m - 1);
    mint iz = mint(z).inv();
    for (int i = 0; i < n + m - 1; i++) a[i] *= iz;
    return a;
}

template <unsigned int mod = 998244353,
          class T,
          std::enable_if_t<internal::is_integral<T>::value>* = nullptr>
std::vector<T> convolution(const std::vector<T>& a, const std::vector<T>& b) {
    int n = int(a.size()), m = int(b.size());
    if (!n || !m) return {};

    using mint = static_modint<mod>;
    std::vector<mint> a2(n), b2(m);
    for (int i = 0; i < n; i++) {
        a2[i] = mint(a[i]);
    }
    for (int i = 0; i < m; i++) {
        b2[i] = mint(b[i]);
    }
    auto c2 = convolution(move(a2), move(b2));
    std::vector<T> c(n + m - 1);
    for (int i = 0; i < n + m - 1; i++) {
        c[i] = c2[i].val();
    }
    return c;
}

std::vector<long long> convolution_ll(const std::vector<long long>& a,
                                      const std::vector<long long>& b) {
    int n = int(a.size()), m = int(b.size());
    if (!n || !m) return {};

    static constexpr unsigned long long MOD1 = 754974721;  // 2^24
    static constexpr unsigned long long MOD2 = 167772161;  // 2^25
    static constexpr unsigned long long MOD3 = 469762049;  // 2^26
    static constexpr unsigned long long M2M3 = MOD2 * MOD3;
    static constexpr unsigned long long M1M3 = MOD1 * MOD3;
    static constexpr unsigned long long M1M2 = MOD1 * MOD2;
    static constexpr unsigned long long M1M2M3 = MOD1 * MOD2 * MOD3;

    static constexpr unsigned long long i1 =
        internal::inv_gcd(MOD2 * MOD3, MOD1).second;
    static constexpr unsigned long long i2 =
        internal::inv_gcd(MOD1 * MOD3, MOD2).second;
    static constexpr unsigned long long i3 =
        internal::inv_gcd(MOD1 * MOD2, MOD3).second;

    auto c1 = convolution<MOD1>(a, b);
    auto c2 = convolution<MOD2>(a, b);
    auto c3 = convolution<MOD3>(a, b);

    std::vector<long long> c(n + m - 1);
    for (int i = 0; i < n + m - 1; i++) {
        unsigned long long x = 0;
        x += (c1[i] * i1) % MOD1 * M2M3;
        x += (c2[i] * i2) % MOD2 * M1M3;
        x += (c3[i] * i3) % MOD3 * M1M2;
        // B = 2^63, -B <= x, r(real value) < B
        // (x, x - M, x - 2M, or x - 3M) = r (mod 2B)
        // r = c1[i] (mod MOD1)
        // focus on MOD1
        // r = x, x - M', x - 2M', x - 3M' (M' = M % 2^64) (mod 2B)
        // r = x,
        //     x - M' + (0 or 2B),
        //     x - 2M' + (0, 2B or 4B),
        //     x - 3M' + (0, 2B, 4B or 6B) (without mod!)
        // (r - x) = 0, (0)
        //           - M' + (0 or 2B), (1)
        //           -2M' + (0 or 2B or 4B), (2)
        //           -3M' + (0 or 2B or 4B or 6B) (3) (mod MOD1)
        // we checked that
        //   ((1) mod MOD1) mod 5 = 2
        //   ((2) mod MOD1) mod 5 = 3
        //   ((3) mod MOD1) mod 5 = 4
        long long diff =
            c1[i] - internal::safe_mod((long long)(x), (long long)(MOD1));
        if (diff < 0) diff += MOD1;
        static constexpr unsigned long long offset[5] = {
            0, 0, M1M2M3, 2 * M1M2M3, 3 * M1M2M3};
        x -= offset[diff % 5];
        c[i] = x;
    }

    return c;
}

}  // namespace atcoder

using namespace atcoder;

using mint=modint998244353;
//using mint=modint1000000007;

template<int mod>
struct nCr{
    vector<static_modint<mod>> fac,inv,ifac;
    void calc(int n){
        fac.resize(n+1),inv.resize(n+1),ifac.resize(n+1);
        fac[0]=inv[1]=ifac[0]=1;
        for(int i=1; i<=n; ++i) fac[i]=fac[i-1]*static_modint<mod>::raw(i);
        for(int i=2; i<=n; ++i) inv[i]=inv[mod%i]*static_modint<mod>::raw(mod-mod/i);
        for(int i=1; i<=n; ++i) ifac[i]=ifac[i-1]*inv[i];
    }
    static_modint<mod> C(int n, int m){
        if(m<0||m>n) return 0;
        return fac[n]*ifac[m]*ifac[n-m];
    }
};

nCr<998244353> de;

void ahcorz(){
    // (a_i - j)! / (a_i - i)! (a_i = a_j)
    // (a_i - j - 1)! / (a_i - i)! * (i - j) (a_i != a_j)
    int n; cin >> n;
    de.calc(n+1);
    vi a; a.pb(0);
    rep(n){
        int x; cin >> x;
        a.pb(max(a.back(),x));
    }
    vc<mint> dp(n+1),aux(n+1);
    auto solve=[&](auto &self, int l, int r) -> void{
        if(l+1==r){
            if(l==0) dp[l]=-1;
            else dp[l]+=aux[l]*l;
            dp[l]*=de.ifac[a[l]-l];
            return;
        }
        int mid=l+r>>1;
        self(self,l,mid);
        if(a[mid]==a[mid-1]){
            int x=mid-1,y=mid;
            while(x-1>=l&&a[x-1]==a[mid]) x--;
            while(y+1<r&&a[y+1]==a[mid]) y++;
            mint tot,tot1,tot2;
            rep(i,x,mid) tot+=dp[i]*de.fac[a[mid]-i],tot1+=dp[i]*de.fac[a[mid]-i-1],tot2+=dp[i]*de.fac[a[mid]-i-1]*i;
            rep(i,mid,y+1) dp[i]-=tot-(tot1*i-tot2);
        }
        vc<mint> vec;
        rep(i,a[mid]-mid,a[r-1]-(l+1)+1) vec.pb(de.fac[i]);
        vc<mint> vec1,vec2;
        rep(i,l,mid) vec1.pb(dp[i]),vec2.pb(dp[i]*i);
        auto res1=convolution(vec,vec1),res2=convolution(vec,vec2);
        int base=a[mid]-mid+l+1;
        rep(i,mid,r) if(a[i]-base>=0&&a[i]-base<sz(res1)) aux[i]-=res1[a[i]-base],dp[i]+=res2[a[i]-base];
        self(self,mid,r);
    };
    solve(solve,0,n+1);
    print(dp[n].val());
}

signed main(){
    ios_base::sync_with_stdio(0),cin.tie(0);
    cout << fixed << setprecision(20);
    int t=1;
    cin >> t;
    while(t--) ahcorz();
}

For a given center coordinate $$$(x,y)$$$, we can model the objective function $$$r=f(x,y)$$$ to maximize as follows.

Formally, this can be modeled as follows:

This is a second order cone program. Generally, this is not as simple to solve as linear or quadratic programs. There are multiple solvers out there, but all of them are either commercial or simply unfit for use on Codeforces. And even if we use general approaches to second order cone programming, their time complexity is at least $$$\mathcal{O}(n^{3.5})$$$, so they cannot work. Almost all general approaches to convex programming do not help very much for this task also, because of the following reasons.

• Gradient Descent cannot work in this task. The objective function is not smooth.

• Coordinate Descent also cannot work in this task for the same reason, and it is not hard to find a countercase.

• Subgradient methods can solve this task, but they take $$$\mathcal{O}(1/\epsilon^2)$$$ iterations to converge. This is a very big dependency on the precision, so they take too much time.

• We do not expect anyone to write Adaptive Coordinate Descent during contest time, but we still tested the PRAXIS algorithm and checked that it does not pass.

• Using nested ternary searches does not help very much. The time complexity will be $$$\mathcal{O}(n \log^2 (1/\epsilon))$$$, but the constants are large due to multiple function calls and floating point operations.

• Heuristics such as the Nelder-Mead method are not proven to converge. In many cases we found it not converging successfully.

In the editorial, we will explain a solution of expected $$$\mathcal{O}(n)$$$ time complexity, with constants depending on the number of dimensions (which is $$$2$$$ in our case).

First, we observe that any answer can be described as a "basis" of at most $$$3$$$ selected circles. For $$$k=0,1,2,3$$$, the basis is as follows.

• Case 1: $$$k=0$$$

This is the case of no circles, which can be regarded as an "identity element" of bases. Some very huge circle that will enclose any given circle, for example the circle with $$$10^{18}$$$ as radius and $$$(0,0)$$$ as center, can represent this case.

• Case 2: $$$k=1$$$

This is the case of a single circle. The circle that represents this case is the one selected circle.

• Case 3: $$$k=2$$$

This is the case of two circles, for which the basis is the largest circle in the intersection of two circles. We can find this by choosing the center as the midpoint of the two points $$$A$$$ and $$$B$$$, where $$$A$$$ and $$$B$$$ are the points where the line segment between circle centers and the circle itself intersect.

• Case 4: $$$k=3$$$

This is the case of three circles, and the most tricky of all four cases. It can be found as one solution to the following system of quadratic equations:

This can be solved algebraically. If you are used to solving geometry problems in Olympiads, you may know the ''Problem of Apollonius''. This is one special case of the problem, which is not very often mentioned because often the three circles do not intersect with each other (thus most of the time one solution for $$$r$$$ must be negative). Or if one does not know the problem, they can find that the locus of the circle center that meets with two circle edges (as in Case 3) is a conic section, precisely one side of a pair of hyperbola. By finding the intersections of two hyperbola, one can find the center of this circle. Thus, this circle can be found in $$$\mathcal{O}(1)$$$ time, with constants based on number of dimensions.

By the system of quadratic equations stated above, we see that there are at most $$$2$$$ solutions. It is sufficient to take the one that happens to be inside the intersection. (If there are two such solutions, take the larger one. For the current version of the data this check is not necessary, but it does not hurt to try.) Thus, for some $$$n>3$$$, the bases can be represented with some $$$k \le 3$$$ circles.

Do note that, already, we have an $$$\mathcal{O}(n^3)$$$ solution based on this. We enumerate all possible bases, and find the smallest one out of them (since that one will be the one that satisfies the conditions).

Now, for some basis circle $$$(x,y,r)$$$, we can check whether some given circle $$$(x_i,y_i,r_i)$$$ is "violated" by this basis (i.e. this basis is not inside this circle) in $$$\mathcal{O}(1)$$$ by comparing the distance. We take an incremental approach. We add circles to the basis one by one, up to $$$3$$$ circles. We choose to change the basis if only the next added circle is violated by the current basis. Of course, still this takes $$$\mathcal{O}(n^3)$$$ time, and sorting the circles based on any argument will not help anyways.

However, adding the circles in random order will make it only take expected $$$\mathcal{O}(n)$$$ time. This can be analyzed by the probability that a new basis will be added. The precise analysis for the time complexity is left as a practice for the reader.

If you have seen the minimum enclosing circle problem, the Welzl's algorithm to solve that precise problem will seem very similar to this. In fact, the suggested algorithm itself is not very different from Welzl's algorithm. If you want, though, you may take an iterative approach instead of modifying Welzl's algorithm. Using three nested loops will do.

There is only two issues left. The first is the issue of numerical instability. Sometimes, due to numerical instability, the algorithm will return a NaN value. It is not that hard to solve, we can simply shuffle again and rerun the algorithm. The given time limit will be sufficient for doing this unless the constant is too big. The second is more tricky, and it is about hacks.

If you use a fixed seed for randomization (or time-based seeds to some extent), someone may hack you by adding an adversarial test case which makes the time complexity explode back to $$$\mathcal{O}(n^3)$$$. This is very bad. How do we solve this? To intervent this, we will make the algorithm halt when the number of iterations exceed a certain limit. Formally, let us choose a constant $$$c$$$, and the algorithm will halt and rerun when the number of iterations exceeds $$$c \cdot n$$$. Then, if the probability of the algorithm successfully running in this number of iterations is $$$p$$$, the expected number of reruns needed is $$$\mathcal{O}(1/p)$$$, and hacking is much harder. The algorithm will successfully find the solution in $$$\mathcal{O}((c/p) \cdot n)$$$ time. Of course, the probability $$$p$$$ depends on $$$c$$$, and you must tune the value as needed. Empirically $$$c=30$$$ runs very well, almost always taking no longer than $$$0.4$$$ seconds under proper optimizations, and $$$1.5$$$ seconds without.

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
 
using lf=long double;
using pt=pair<lf,lf>;
lf& real(pt& p){return p.first;}
lf& imag(pt& p){return p.second;}
pt midp(pt a,pt b){return pt{(real(a)+real(b))/2,(imag(a)+imag(b))/2};}
pt addi(pt a,pt b){return pt{(real(a)+real(b)),(imag(a)+imag(b))};}
pt subt(pt a,pt b){return pt{(real(a)-real(b)),(imag(a)-imag(b))};}
pt mult(pt a,lf b){return pt{real(a)*b,imag(a)*b};}
lf abs(pt a){return sqrtl(powl(real(a),2)+powl(imag(a),2));}
lf dist(pt a,pt b){return sqrtl(powl(real(a)-real(b),2)+powl(imag(a)-imag(b),2));}
 
struct circ{pt p;lf r;};
const lf inf=1e18;
 
circ basis0(){return {pt{0,0},inf};}
 
circ basis1(circ a){return a;}
 
circ basis2(circ a,circ b)
{
    pt aa=a.p,bb=b.p;
    pt ab=subt(bb,aa),ba=subt(aa,bb);
    lf aab=abs(ab),aba=abs(ba);
    real(ab)/=aab;
    imag(ab)/=aab;
    real(ba)/=aba;
    imag(ba)/=aba;
    pt ar=addi(aa,mult(ab,a.r)),br=addi(bb,mult(ba,b.r));
    
    return {midp(ar,br),dist(ar,br)/2.0L};
}
 
circ basis3(circ a,circ b,circ c)
{
    lf x1=real(a.p),y1=imag(a.p),r1=a.r;
    lf x2=real(b.p),y2=imag(b.p),r2=b.r;
    lf x3=real(c.p),y3=imag(c.p),r3=c.r;
    lf a2=x1-x2,a3=x1-x3,b2=y1-y2,b3=y1-y3,c2=r2-r1,c3=r3-r1;
    lf d1=x1*x1+y1*y1-r1*r1,d2=d1-x2*x2-y2*y2+r2*r2,d3=d1-x3*x3-y3*y3+r3*r3;
    lf ab=a3*b2-a2*b3;
    lf xa=(b2*d3-b3*d2)/(ab*2)-x1;
    lf xb=(b3*c2-b2*c3)/ab;
    lf ya=(a3*d2-a2*d3)/(ab*2)-y1;
    lf yb=(a2*c3-a3*c2)/ab;
    lf A=xb*xb+yb*yb-1;
    lf B=2*(r1+xa*xb+ya*yb);
    lf C=xa*xa+ya*ya-r1*r1;
    lf r=-(A?(B-sqrtl(B*B-4*A*C))/(2*A):C/B);
    return {pt{x1+xa+xb*r,y1+ya+yb*r},r};
}
 
bool viol(circ p,circ a)
{
    return a.r<p.r+dist(a.p,p.p);
}
 
circ solve(vector<circ>&v)
{
    lf _nan=nan("aaa");
    mt19937_64 mt(1999999);
    //shuffle(begin(v),end(v),mt);
    vector<circ>basis;
    auto trivial=[&]()
    {
        if(size(basis)==0)return basis0();
        if(size(basis)==1)return basis[0];
        if(size(basis)==2)return basis2(basis[0],basis[1]);
        return basis3(basis[0],basis[1],basis[2]);
    };
 
    int counter=0;
    
    auto rec=[&](auto rec,int n)->circ
    {
        if(n==0||size(basis)==3)return trivial();
        counter++;
        if(counter>30*size(v))return {pt{0,0},_nan};
        auto c=rec(rec,n-1);
        auto p=v[n-1];
        if(!viol(c,p)||isnan(c.r))return c;
        basis.push_back(p);
        c=rec(rec,n-1);
        basis.pop_back();
        return c;
    };
    auto c=rec(rec,size(v));
    while(isnan(c.r))
    {
        counter=0;
        shuffle(begin(v),end(v),mt);
        c=rec(rec,size(v));
    }
    return c;
}
 
int main()
{
    cin.tie(0)->sync_with_stdio(0);
    int n;cin>>n;
    vector<circ>v(n);
    for(auto&[p,r]:v)
    {
        ll x,y,rr;cin>>x>>y>>rr;
        p={x,y};r=rr;
    }
    auto ans=solve(v);
    cout<<setprecision(16)<<fixed<<real(ans.p)<<" "<<imag(ans.p)<<" "<<ans.r<<"\n";
}