573484A - The Last Number Standing
Problem Credits: youssef_fdln, rayenbbs
Let us analyze the behavior of the $$$GCD$$$ operation:
- The $$$GCD$$$ of two numbers is an associative operation, which means the order in which we compute the $$$GCD$$$ does not affect the final result.
- The $$$GCD$$$ operation satisfies the property: $$$GCD(a, b, c) = GCD(GCD(a, b), c)$$$
- Therefore, if we keep applying the $$$GCD$$$ operation to all elements of the array, the final result will always be the $$$GCD$$$ of the entire array.
Thus, no matter how we choose and pair elements during the process, the final result is the $$$GCD$$$ of all elements in the initial array. This means the number of unique final results is always $$$1$$$.
#include<bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
int ans = a[0];
for (int i = 1; i < n; i++)
ans = gcd(ans, a[i]);
cout << 1 << '\n' << ans << '\n';
return 0;
}
573484B - Monitors
Problem Credits: 9mi7a
The problem has a monotonic structure:
If it is possible to power $$$x$$$ monitors, it is also possible to power any number less than $$$x$$$
If it is impossible to power $$$x+1$$$ monitors, it is also impossible to power any number greater than $$$x$$$.
Since the problem is monotonic, we can use binary search over the range $$$[1, n]$$$ to find the maximum $$$x$$$ such that $$$x$$$ monitors can be powered with $$$m$$$ batteries.
For each midpoint $$$x$$$ in the binary search, calculate the total number of batteries required to power the first $$$x$$$ monitors.
If the total number of batteries is less than or equal to $$$m$$$, then it is possible to power $$$x$$$ monitors, and we search for a larger value. Otherwise, we search for a smaller value.
The solution runs in $$$O(Q.log(n))$$$.
#include <bits/stdc++.h>
using namespace std;
void solve() {
long long n, m;
cin >> n >> m;
long long l = 1, r = n;
long long ans = 0;
while (l <= r) {
long long x = (l + r) / 2;
long long nb = m / x;
long long v = nb * nb + 3 * nb;
if (v >= x) {
l = x + 1;
ans = x;
} else {
r = x - 1;
}
}
cout << ans << '\n';
}
int main() {
int Q;
cin >> Q;
while (Q--) {
solve();
}
}
573484C - The Detective Boys' Duel
Problem Credits: rayenbbs
Case 1: Players start in the same column ($$$x_1 = x_2$$$)
When both players start in the same column, the game reduces to a sequence of moves closer to each other.
Since the game has a strict turn-by-turn rule: - The number of positions between Ayumi and Mitsuhiko determines the winner. - Let $$$d = y_1 - y_2 - 1$$$, the number of positions between the two players.
- If $$$d$$$ is odd, the player who moves second wins.
- The first player will have the last turn, finding themself in a blocked state.
- If $$$d$$$ is even, the player who moves first wins.
- The second player will have the last turn, finding themself in a blocked state.
Case 2: Players start in different columns ($$$x_1 \neq x_2$$$)
If Ayumi and Mitsuhiko are initially in different columns, the first player can move to the opponent's column and adjust their $$$y$$$-coordinate optimally.
Because the first player to move can adjust his $$$y$$$-coordinate, they can choose whether to make the number of positions between him and his opponent odd or even, thus, they can determine the outcome of the game.
After this, the position is reduced to Case 1.
By playing optimally, they will always win.
#include<bits/stdc++.h>
using namespace std;
int main() {
int x1, y1, x2, y2, t;
cin >> x1 >> y1 >> x2 >> y2 >> t;
if (x1 != x2) {
if (t == 1) {
cout << "Ayumi" << '\n';
} else cout << "Mitsuhiko" << '\n';
} else {
int positionsBetweenAyumiAndMitsuhiko = y1 - y2 - 1;
if (t == 1) {
if (positionsBetweenAyumiAndMitsuhiko % 2 != 0) {
cout << "Mitsuhiko" << '\n';
} else cout << "Ayumi" << '\n';
} else {
if (positionsBetweenAyumiAndMitsuhiko % 2 != 0) {
cout << "Ayumi" << '\n';
} else cout << "Mitsuhiko" << '\n';
}
}
}
573484D - The Dart's Dance
Problem Credits: Gassouma0, get_ducked
This problem can be reduced to the balanced brackets problem (where > corresponds to ( and < corresponds to )) with an additional condition:
If the last element of the string is < and the rest of the string (excluding the last element) forms a balanced sequence, the output should still be "SUCCESS". This accounts for a final unmatched < panel that can reflect the dart and break, in this case all panels are broken even though the the sequence is not balanced.
To solve this problem we process the string character by character, maintaining a balance counter:
- When the dart encounters a
>panel, it passes through the panel without breaking it so we increment the counter. - When the dart encounters a
<panel, it breaks the panel and reflects off it and starts moving leftward. If the dart had already traversed one or more>panels, it will reflect off the last rightward panel breaking it in the process and the dart start moving rightward again therefore, we decrement the counter to account for the broken>panel.
While processing the panels:
- If the counter becomes negative at any point except the end of the string, it means the dart cannot continue as there are unmatched
<panels, and we output"FAILURE". - Special corner case: If the counter is
-1at the end of the string (indicating the dart's trajectory ends on the last panel left which is<), we treat this as a valid state and output"SUCCESS". This is because the dart can reflect off the final<panel and break it, ensuring all panels are destroyed, even though the sequence is not balanced. - If the counter is
0after processing all panels, output"SUCCESS". - If the counter is positive after processing all panels, it means there are unmatched
>panels, and we output"FAILURE".
#include<bits/stdc++.h>
using namespace std;
int main() {
int t, n;
cin >> t;
while (t--) {
cin >> n;
string S;
cin >> S;
int n = S.size();
int i, counter = 0;
for (i = 0; i < n; i++) {
if (S[i] == '<')
counter--;
else
counter++;
if (counter < 0)
break;
}
if (counter == 0)
cout << "SUCCESS\n";
else if ((counter == -1) && (i == n - 1))
cout << "SUCCESS\n";
else
cout << "FAILURE\n";
}
}
573484E - Countdown to Heaven
Problem Credits: wapiex
Since the number $$$n$$$ is too big ( $$$1 \le n\le 10^{(10^7)}$$$ ), we need to read it as a string. To check divisibility by $$$3$$$ and $$$9$$$, we simply compute the sum of its digits and check whether or not its divisible by $$$3$$$ or $$$9$$$ (divisibility rule for $$$3$$$ and $$$9$$$).
Now to check divisibility by $$$2^k$$$:
- For divisibility by $$$2$$$, we only need the last digit.
- For divisibility by $$$4$$$, we need to check the last 2 digits.
- In general, for divisibility by $$$2^k$$$, we need the last $$$k$$$ digits.
So we only need to extract the last $$$18$$$ digits of the string and then check for the largest $$$2^k$$$ that divides the extracted number, because $$$0 \leq k \leq 18$$$, and the last $$$18$$$ digits can fit in $$$long long$$$ data type in $$$C++$$$.
#include<bits/stdc++.h>
using namespace std;
int main() {
string n;
cin >> n;
int sum = 0;
for (int i = 0; i < n.size(); i++) {
sum += n[i] - '0';
}
int t = 0;
if (sum % 9 == 0) t = 2;
else if (sum % 3 == 0)t = 1;
long long cur = 0;
long long f = 1;
for (int i = n.size() - 1; i >= max(0, (int) n.size() - 18); i--) {
cur = cur + (n[i] - '0') * f;
f *= 10;
}
// edge case when there are a lot of tailing zeros
if (cur == 0) cur = f;
// divisibility by 2^k
long long mxk = 1, k = 2;
int ans = 0;
while (k < cur) {
if (cur % k == 0) {
mxk = k;
ans++;
} else break;
k *= 2;
}
// even if (k>18) we won't take it into account
cout << min(18, ans) << " " << t << endl;
return 0;
}
573484F - Hotspot Hunt
Mapping Places to Zones:
- Since every place belongs to exactly one zone, we need a data structure to map each place to its corresponding zone. Use a dictionary (or map in C++):
place_to_zone: map<string, string>
Tracking Zone Crime Totals:
- Use another dictionary to store the total number of crimes reported in each zone:
zone_to_crimes: map<string, int>
- For each crime record, use the first dictionary to get the correspoinding zone, and then update the total for that zone.
Finding the Maximum:
- After processing all records, iterate through the second dictionary (
zone_to_crimes) to find the zone with the highest total crimes. Since the problem guarantees a unique answer, no tie-breaking is required.
#include<bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
map <string, string> m1; // to map each place to a zone
map<string, int> m2; // to store number of crimes in each zone
for (int i = 0; i < n; i++) {
string place, zone;
cin >> place >> zone;
m1[place] = zone;
}
int q;
cin >> q;
for (int i = 0; i < q; i++) {
string s;
int x;
cin >> s >> x;
m2[m1[s]] += x;
}
int maxi = 0;
string ans = "";
for (auto el: m2) {
if (el.second > maxi) {
maxi = el.second;
ans = el.first;
}
}
cout << ans << endl;
}
573484G - Dr.Agasa's Glasses
Problem Credits: ilefbenrahma
The problem is challenging enough that we couldn't come up with a proper solution for it.
573484H - Secret Network
Problem Credits: CMiner, get_ducked
Key Observations:
The lexicographically largest binary string of the same length as a given string $$$s$$$ is the string containing all 1s. For example, if $$$s$$$ has a length of $$$4$$$, the largest binary string is $$$1111$$$.
The number of binary strings between two binary strings $$$S_1$$$ and $$$S_2$$$ is equivalent to converting both strings to numbers and calculating the difference. For example, if $$$s = 100$$$, the number of strings in the interval $$$]100, 111]$$$ is $$$7 - 4 = 3$$$.
The input string may be too large to store as a numeric variable in most programming languages.
A brute-force approach, generating all lexicographically larger strings, would result in a worst-case scenario of $$$2^{(10^6+1)} - 1$$$ strings, which is computationally infeasible.
Solution Approach:
An important thing to notice is the fact that the result must be computed modulo $$$2^{62}$$$. This allows us to simplify the calculation by only focusing on the remainder.
The remainder of a binary number modulo $$$2^k$$$ is determined by its rightmost $$$k$$$ bits. For example:
- $$$101100 \mod 2^3 = 100 = 4$$$.
Therefore, we only need to calculate the last $$$62$$$ bits of the binary string representing the difference between $$$S$$$ and the largest string of the same length. This can be illustrated with the following example where $$$s_{largest} = 111111$$$, $$$s = 101100$$$ and the result equals $$$010011$$$:
111111
-
101100
---------
010011
Algorithm Steps:
- Start from the rightmost $$$62$$$ bits of the string (or the entire string if its length is less than $$$62$$$).
- Calculate the difference between $$$s_{largest}$$$ and $$$s$$$, and then convert it from binary to decimal. Or even better, whenever $$$s[i] = 0$$$, we add $$$2^i$$$ to the final result.
#include<bits/stdc++.h>
using namespace std;
int main() {
int t, n;
string s;
cin >> t;
while (t--) {
cin >> n;
cin >> s;
// Solution 1: Left-shift and bitwise OR approach
long long res = 0;
for (int i = max(0, n - 62); i < n; i++) {
res <<= 1;
if (s[i] == '0')
res |= 1;
}
// Solution 2: Explicit addition and powers of 2 approach
res = 0;
long long k = 1;
for (int i = n - 1; i >= max(0, n - 62); i--) {
if (s[i] == '0')
res += k;
k *= 2;
}
cout << res << endl;
}
}
573484I - Symmetry of Love
Problem Credits: moncef12, get_ducked
A string is a palindrome if its first half mirrors its second half.
For each mismatched pair of characters $$$s[i]$$$ and $$$s[n−i−1]$$$, the cost of transforming them to match is: $$$cost=min(abs(s[i]−s[n−i−1]),26−abs(s[i]−s[n−i−1]))$$$
This accounts for wrapping around the alphabet (e.g., z→a).
Two main options for achieving a palindrome:
- Transform $$$S$$$ into a palindrome without erasing any letter.
- Erase one letter and then transform the remaining substring into a palindrome.
To minimize cost efficiently, we use prefix sums to precompute costs for transformations.
Approach:
1. Precomputations:
- Calculate prefix sums for the cost of making $$$S$$$ a palindrome:
- From the left:
prefix - From the right ( reversed $$$S$$$):
prefixReversed
- From the left:
- Additionally, compute "Shifted" prefix sums for considering substring palindromes when a letter is erased:
- From the left:
prefixShifted - From the right ( reversed $$$S$$$):
prefixShiftedReversed
- From the left:
2. Calculate Costs Without Erasing:
- Use the precomputed prefix sums to directly determine the cost of transforming $$$S$$$ into a palindrome.
3. Calculate Costs With Erasing:
- For each possible position to erase, compute the cost of making the remaining substring a palindrome using the prefix sums. Add the erasing cost $$$m$$$.
4. Minimize the Total Cost:
- Iterate through all possible cases to find the minimum cost.
Corner Case: if $$$n = 2$$$, we need to take the minimum cost between transforming $$$S$$$ versus erasing one letter.
The overall time complexity is $$$O(n)$$$.
#include<bits/stdc++.h>
using namespace std;
int main() {
string s;
int n;
cin >> n;
cin >> s;
int m;
cin >> m;
string reversedS = s;
reverse(reversedS.begin(), reversedS.end());
vector<int> prefix;
vector<int> prefixReversed;
vector<int> prefixShifted;
vector<int> prefixShiftedReversed;
prefix.push_back(0);
prefixReversed.push_back(0);
prefixShifted.push_back(0);
prefixShiftedReversed.push_back(0);
for (int i = 0; i < (n + 1) / 2; i++) {
prefix.push_back(prefix.back() + min(abs(s[i] - s[n - i - 1]), 26 - abs(s[i] - s[n - i - 1])));
}
for (int i = 0; i < (n + 1) / 2; i++) {
prefixReversed.push_back(prefixReversed.back() + min(abs(reversedS[i] - reversedS[n - i - 1]),
26 - abs(reversedS[i] - reversedS[n - i - 1])));
}
for (int i = 1; i < (n + 1) / 2; i++) {
prefixShifted.push_back(prefixShifted.back() + min(abs(s[i] - s[n - i]), 26 - abs(s[i] - s[n - i])));
}
for (int i = 1; i < (n + 1) / 2; i++) {
prefixShiftedReversed.push_back(prefixShiftedReversed.back() + min(abs(reversedS[i] - reversedS[n - i]),
26 - abs(reversedS[i] - reversedS[n - i])));
}
int ans = prefix.back();
for (int i = 1; i < (n + 1) / 2; i++) {
int l, r;
r = prefixShifted.size() - 1;
l = i;
int x1 = prefix[i - 1] + prefixShiftedReversed[r] - prefixShiftedReversed[l - 1] + m;
int x2 = prefixReversed[i - 1] + prefixShifted[r] - prefixShifted[l - 1] + m;
ans = min(ans, x1);
ans = min(ans, x2);
}
if (n == 2) {
ans = min(ans, m);
}
cout << ans << endl;
}
573484J - Shrinking Mystery
Problem Credits: Dali358
To determine the list of drink types that could possibly be poisoned, excluding all the safe drink types, we will not focus on the guests who shrank because they may have consumed both safe and poisoned drinks, therefore, the only drinks we can definitively mark as safe are those consumed by guests who did not shrink.
Any drink type that isn't marked as safe is considered potentially poisoned, this includes drink types that were not served.
The only corner case to look out for is when all drinks have been marked as safe, we will then output $$$-1$$$.
To efficiently solve this problem, we will use an Ordered/Hash Set data structure (or *boolean array) to store all drinks that are safe. Let's denote $$$A$$$ the number of these safe drinks; when we loop through all drink types we can figure out wether the $$$i$$$-th type is safe in $$$O(log(A))$$$ for ordered sets or $$$O(1)$$$ for hash sets and boolean arrays.
#include<bits/stdc++.h>
using namespace std;
int main() {
int N, M;
cin >> N >> M;
vector <vector<int>> drinks(N);
for (int i = 0; i < N; i++) {
int K;
cin >> K;
for (int j = 0; j < K; j++) {
int x;
cin >> x;
drinks[i].push_back(x);
}
}
string S;
cin >> S;
set<int> safe_drinks;
for (int i = 0; i < N; i++) {
for (int j = 0; j < (int) drinks[i].size(); j++) {
if (S[i] == '0') {
safe_drinks.insert(drinks[i][j]);
}
}
}
if (safe_drinks.size() == M) {
cout << -1 << '\n';
return 0;
}
for (int i = 1; i <= M; ++i) {
if (safe_drinks.contains(i)) continue;
cout << i << " ";
}
cout << '\n';
return 0;
}
573484K - Robot Toy Tactics
Problem Credits: BFR
There are multiple robot toys (let's say $$$N$$$) on the grid, and multiple robots can occupy the same cell. On each turn, a player can move only one robot toy. So the game can be viewed as $$$N$$$ different grids, each containing one single robot toy.
This game is an impartial game: the set of possible moves is the same for both players, there is no hidden information, the game is finite, and the only difference between the 2 players is that one of them plays first.
So to check whether or not Ran (the first player) is in a winning position, we are going to use the Sprague-Grundy Theorem.
The game ends when a player cannot make a legal move, and the other player is declared the winner.
We have to find the Sprague-Grundy number for each game (the Sprague-Grundy value for each cell that has a robot toy on it).
The Sprague-Grundy number of a losing position is $$$0$$$. Therefore, each cell where a robot toy will be blocked in the cell directly above it and in the cell directly to its left by the limits of the grid or a barrier has a Sprague-Grundy value of $$$0$$$. To get the Sprague-Grundy values of the other cells, we need to recursively move to the reachable states of every cell and find their Sprague-Grundy numbers. Let's call this set $$$X$$$. The Sprague-Grundy number of the current state is the minimum non-negative number that is not present in the set $$$X$$$ (mex). For example, if $$$X = {0, 2, 3}$$$, then the Sprague-Grundy number of this current state is $$$1$$$.
Reachable states from every cell are all the cells above the current cell and the cells to the left of the current cell before reaching the limit of the grid.
We also need to store the Sprague-Grundy value of each cell in a 2D array as we compute it, to avoid recalculating the value multiple times.
After finding the Sprague-Grundy numbers of each game state (a grid with one robot toy tactic), we need to XOR them, since each each grid is considered as an independent game, If the resulting value is different from $$$0$$$, then Ran (the first player) is in a winning state. Otherwise, if the resulting value is $$$0$$$, Ran will lose.
For more intuition about the Sprague-Grundy Theorem, you can check this blog.
The total time complexity of the described solution is $$$O(n*m*(n+m))$$$.
#include <bits/stdc++.h>
using namespace std;
int SG[101][101]; // array to store Sprague-Grundy values
char grid[101][101];
bool blocked(int i, int j) {
return (i == 0 || (i > 0 && grid[i - 1][j] == '+')) && (j == 0 || (j > 0 && grid[i][j - 1] == '+'));
}
int mex(set<int> &s) {
int i = 0;
for (auto x: s) {
if (x != i) return i;
i++;
}
return i;
}
int calculate_sg(int i, int j) {
if (blocked(i, j)) {
return SG[i][j] = 0;
}
if (SG[i][j] != -1) {
return SG[i][j];
}
set<int> states;
int k = i - 1;
while (k >= 0 && grid[k][j] != '+') {
states.insert(calculate_sg(k, j));
k--;
}
k = j - 1;
while (k >= 0 && grid[i][k] != '+') {
states.insert(calculate_sg(i, k));
k--;
}
return SG[i][j] = mex(states);
}
int main() {
vector<pair<int, int>> positions;
memset(SG, -1, sizeof SG);
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
for (int j = 0; j < m; j++) {
grid[i][j] = s[j];
if (s[j] == '!') positions.push_back({i, j});
}
}
int res = 0;
for (auto x: positions) {
res = res ^ calculate_sg(x.first, x.second);
}
if (res == 0) {
cout << "NO" << endl;
} else {
cout << "YES" << endl;
}
}
573484L - Shadows in the Triangle
Problem Credits: Z41_1n
The area $$$A$$$ of a triangle given two sides $$$a$$$ and $$$b$$$ with an included angle $$$\theta$$$ is given by:
$$$A = \frac{1}{2} \times a \times b \times \sin(\theta)$$$
The maximum area is achieved when $$$\sin(\theta) = 1$$$, which occurs when $$$\theta = 90^\circ$$$. Hence, the maximum area is:
$$$A_{\text{max}} = \frac{1}{2} \times a \times b$$$
#include<bits/stdc++.h>
using namespace std;
void solve() {
double a, b;
cin >> a >> b;
cout << ((a * b) / 2.0) << '\n';
}
int main() {
int t;
cin >> t;
while (t--) {
solve();
}
}
573484M - The Phantom's Hidden Pattern
Problem Credits: boukamcha77
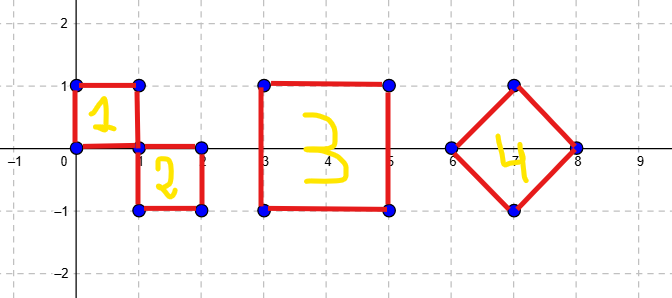
There are only four types of squares that can be formed with the given constraints, based on how the points align across the three horizontal lines ($$$y = 1$$$, $$$y = 0$$$, $$$y = -1$$$). Here’s a figure to illustrate the types of squares:
To efficiently solve the problem, we use three boolean arrays:
- $$$v1[x]$$$: True if there is a point at $$$(x, 1)$$$.
- $$$v2[x]$$$: True if there is a point at $$$(x, 0)$$$.
- $$$v3[x]$$$: True if there is a point at $$$(x, -1)$$$.
These arrays allow us to quickly check the presence of points along each line.
Next, we iterate through all possible $$$x$$$ values from $$$0$$$ to $$$10^6$$$. For each $$$x$$$, we check if it can serve as the starting point of any of the four types of squares (a top-left vertex for types 1, 2, and 3, or a top vertex for type 4):
- Type 1: Check if points $$$(x, 1)$$$, $$$(x+1, 1)$$$, $$$(x, 0)$$$, and $$$(x+1, 0)$$$ exist.
- Type 2: Check if points $$$(x, 0)$$$, $$$(x+1, 0)$$$, $$$(x, -1)$$$, and $$$(x+1, -1)$$$ exist.
- Type 3: Check if points $$$(x, 1)$$$, $$$(x+2, 1)$$$, $$$(x, -1)$$$, and $$$(x+2, -1)$$$ exist.
- Type 4: Check if points $$$(x, 1)$$$, $$$(x+1, 0)$$$, $$$(x, -1)$$$, and $$$(x-1, 0)$$$ exist.
By iterating through all possible $$$x$$$-coordinates and performing these constant-time checks, every square is counted exactly once.
#include<bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
int max_n = 1e6;
// initialize vector sizes to max_n + 2 to avoid any index range problems
vector<bool> v1(max_n + 2, 0), v2(max_n + 2, 0), v3(max_n + 2, 0);
// every represents a line
// v1 d1:y=1
// v2 d2:y=0
// v3 d3:y=-1
// vi[j]=true if there is a point with x=j on the line di
for (int i = 0; i < n; i++) {
int x, y;
cin >> x >> y;
if (y == 1) {
v1[x] = 1;
}
else if (y == 0) {
v2[x] = 1;
}
else {
v3[x] = 1;
}
}
int res = 0;
for (int i = 0; i < max_n; i++) {
//type 1 square: y = 1 with y = 0 and square side length is 1
if (v1[i] && v1[i + 1] && v2[i] && v2[i + 1]) {
res++;
}
//type 2 square: y = 0 with y = -1 and square side length is 1
if (v2[i] && v2[i + 1] && v3[i] && v3[i + 1]) {
res++;
}
//type 3 square: y = 1 with y = -1 and side length is 2
if (v1[i] && v3[i] && v1[i + 2] && v3[i + 2]) {
res++;
}
//type 4 square: diagonal square sides
if (i - 1 >= 0 && v1[i] && v2[i + 1] && v3[i] && v2[i - 1]) {
res++;
}
}
cout << res << endl;
}





