I found this question at http://math.stackexchange.com/.
Let n is a positive integer.
n = p1e1p2e2... pkek is the complete prime factorization of n.
Let me define a function f(n)
f(n) = p1c1p2c2... pkck where ck = ek - 1
Example:
72 = 2332, so f(72) = 23 - 132 - 1 = 2231 = 12
144 = 2432, so f(144) = 24 - 132 - 1 = 2331 = 24
Now let
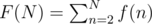
Example: F(10) = 1 + 1 + 2 + 1 + 1 + 1 + 4 + 3 + 1 = 15
Now I want to evaluate F(N) for a fairly large value of N, say 1012. Can I do it without factorizing each number?
It appears quite interesting. I think maybe it requires some kind of inclusion-exclusion, but so far was unable to implement. Any idea how to solve?






