I found this question at http://math.stackexchange.com/.

Let n is a positive integer.

n = p₁^e₁p₂^e₂... p_k^e_k is the complete prime factorization of n.

Let me define a function f(n)

f(n) = p₁^c₁p₂^c₂... p_k^c_k where c_k = e_k - 1

Example:

72 = 2³³², so f(72) = 2^3 - 13^2 - 1 = 2²3¹ = 12

144 = 2⁴³², so f(144) = 2^4 - 13^2 - 1 = 2³3¹ = 24

Now let

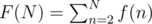
Example: F(10) = 1 + 1 + 2 + 1 + 1 + 1 + 4 + 3 + 1 = 15

Now I want to evaluate F(N) for a fairly large value of N, say 10¹². Can I do it without factorizing each number?

It appears quite interesting. I think maybe it requires some kind of inclusion-exclusion, but so far was unable to implement. Any idea how to solve?