Starting from October 2015 ratings formulas are open. They are given in the post. It is likely that from time to time we will change them slightly, it will be reflected here.
The basic idea of Codeforces rating system is to generalize Elo rating to support games with multiple participants.
Each community member is characterized by value ri — integer number. Roughly speaking, the higher value means better results in the contests. Rating is calculated/recalculated so that the equality strives to be correct:
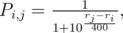
where Pi, j is probability that the i-th participant has better result than the j-th participant. Therefore for two participants the probability to win/lose depends on subtraction of their ratings. For example, if the difference of ratings is equal to 200 then stronger participant will win with probability ~0.75. If the difference of ratings is equal to 400 then stronger participant will win with probability ~0.9.
After a contest the values ri change in a way to satisfy main formula better.
Let’s calculate expected place seedi for each participant before contest. It equals to the sum over all other participants of probabilities to win (to have better place than) the i-th plus one because of 1-based place indices:
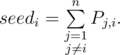
For example, before Codeforces Round 318 [RussianCodeCup Thanks-Round] (Div. 1) tourist had rating 3503 and his seed was ~1.7, and Petr had rating 3029 and expected place ~10.7.
General idea is to increase ri if actual place is better than seedi and to decrease ri if actual place is worse than seedi.
Having seedi and actual place, let’s calculate their geometric mean mi. You can think about it as an something average between seedi and actual place shifted to the better place. Using binary search find such rating value R which the i-th participant should have to have a seedi = mi. Obviously the rating ri should be modified to become closer to R. We use di = (R - ri) / 2 as rating change for the i-th participant.
It's almost all except the phase of fighting against inflation. Inflation works as follows: the rich get richer. We will try to avoid it. If we assume that the rating was already calculated fair (i.e. everybody has perfect statistically based rating) then expected change of rating after a contest is equal to zero for any participant.
Choose a group of the most rated (before the round) participants and decide that their total rating shouldn’t change. We use heuristic value 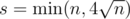 as a size of such group. Let’s find the sum of di over participants from group and adjust all values di (for all participants) to make the sum to be zero. In other words, ri = ri + inc, where inc = - sums / s, sums is sum of di over s participants from chosen group.
as a size of such group. Let’s find the sum of di over participants from group and adjust all values di (for all participants) to make the sum to be zero. In other words, ri = ri + inc, where inc = - sums / s, sums is sum of di over s participants from chosen group.
After the round 327 we restricted the effect in following way. Firstly, we do ri = ri + inc, where inc = - sum(di) / n - 1, sum(di) is sum of all di. It makes the sum of all di to be near zero and non-positive in the same time. Secondly, we apply idea from the previous paragraph, but inc = min(max( - sums / s, - 10), 0). Thus, the effect of modification can not reduce rating for more than ~10 points.
By the way, for any consistent rating the following assertions should be true:
- if the participant A had worse rating than the participant B before the contest and finished the contest on the worse place then after recalculations the the rating of A can’t be greater than the rating of B
- if A finished the contest better than B but A had worse rating before the contest then A should have equal or greater rating change than B.
In particular, formulas are tested to satisfy the both items on each ratings recalculation.
You may read the actual Codeforces code to recalculate ratings here: 13861109.







