Начиная с октября 2015-го года рейинг на Codeforces считается по открытым формулам, о которых и здесь речь.
Вполне вероятно, что мы будем их слегка менять со временем, что будем отражать в этом посте.
Основная концепция используемых формул — мы расширяем принципы рейтинга Эло для встреч более чем двух участников.
Каждый участник характеризуется величиной рейтинга ri — целое число (возможно отрицательное). Грубо говоря, чем это значение выше, тем лучше участник выступает в соревнованиях. Рейтинг это подсчитывается/пересчитывается таким образом, чтобы выполнялось равенство:
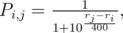
где Pi, j вероятность того, что i-й участник победит на соревновании j-го. Таким образом вероятность победы одного участника над другим определяется только разностью их рейтингов. Например, если разница рейтингов двух участников равна 200, то побеждает сильнейший с вероятностью примерно 0.75. При разнице рейтинго 400 вероятность возрастает до 0.9.
После очередного соренования величины ri меняются так, чтобы в большей степени соответствовать основной формуле рейтинга. В данном случае “вероятность” какое-то расплывчатое понятие, последние соревнования вносят больший вклад в ожидаемый результат.
Рассмотрим момент до начала раунда и посчитаем для каждого участника его ожидаемое место (его называют seedi). Ожидаемое место равно сумме вероятностей по всем другим участникам обойти данного плюс один (плюс один берется из-за 1-индексации). Например, перед Codeforces Round 318 [RussianCodeCup Thanks-Round] (Div. 1) при рейтинге 3503 ожидаемое место у tourist было примерно 1.7, а у Petr при рейтинге 3029 ожидаемое место было примерно 10.7.
Общая идея пересчета рейтинга такова: если участник занимает место ниже своего ожидаемого, то его рейтинг следует убавить, а если участник занимает место выше своего ожидаемого, то его рейтинг следует увеличить.
Посчитаем для участника среднее геометрическое его текущего места и ожидаемого, пусть эта величина равна mi. В самом деле, это какое-то среднее значение между ними, оптимистично сдвинутое в сторону меньшего из мест. Найдем (с помощью бинарного поиска) такой рейтинг R, которым должен бы был иметь этот участник, чтобы всё-таки ожидаемо занимать место mi (среди того же набора участников). Понятно, что текущий рейтинг участника должен быть изменен так, чтобы стремиться к R. Поэтому, изменение рейтинга участника в раунде вычисляется как di = (R - ri) / 3.
Это почти всё, кроме фазы борьбы с инфляцией. Заметим, что при инфляции богатые становятся еще богаче, поэтому будем бороться именно с этим. Если предположить, что рейтинг был уже посчитан справедливо (то есть каждый участник имеет свой статистически обоснованный рейтинг), то математическое ожидание изменения рейтинга по любому участнику должно быть равно 0. Выберем группу наиболее высокорейтинговых участников раунда (по рейтингу ri — до начала раунда) и скажем, что сумма их рейтингов должна остаться неизменной. В качестве размера такой группы выбирается эвристическая величина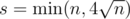 
. Если di таковы, что их сумма для этой группы не равна 0, то ко всем им прибавляется некоторое значение (вычитается) так, чтобы их сумма s наиболее высокорейтинговым участникам стала равна 0.
Кстати, для любого логически непротиворичивого рейтинга должны выполняться несколько инвариантов: если участник A имел рейтинг хуже участника B и выступил хуже него на текущем раунде, то и его рейтинг после пересчета должен быть не лучше чем у B; если A выступил лучше B, но имел до раунда хуже рейтинг, то ему должны прибавить не меньше единиц рейтинга чем участнику B.
В частности, для обновленного рейтинга Codeforces эти инварианты проверяются на выполнение при любом пересчете рейтинга.
