Problem A. PawnChess

Player A wins if the distance of his nearest pawn to the top of the board is less than or equal to the distance of the Player’s B nearest pawn to the bottom of the board (Note that you should only consider pawns that are not blocked by another pawns).

Problem B. The monster and the squirrel

After drawing the rays from the first vertex (n - 2) triangles are formed. The subsequent rays will generate independently sub-regions in these triangles. Let's analyse the triangle determined by vertices 1, i, i + 1, after drawing the rays from vertex i and (i + 1) the triangle will be divided into (n - i) + (i - 2) = n - 2 regions. Therefore the total number of convex regions is (n - 2)²

If the squirrel starts from the region that have 1 as a vertex, then she can go through each region of triangle (1, i, i + 1) once. That implies that the squirrel can collect all the walnuts in (n - 2)² jumps.

Problem C. The Big Race

Let D be the length of the racetrack, Since both athletes should tie DmodB = DmodW.

Let M = lcm(B, W), then D = k·M + r. None of the athletes should give one step further, therefore r ≤ min{B - 1, W - 1, T} = X.

D must be greater than 0 and less than or equal to T so  - r / M < k ≤ (T - r) / M.

For r = 0, the number of valid racetracks is 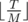, and for r > 0 the number of racetracks is floor((T - r) / M) + 1.

Iterating over all possible r, we can count the number of racetracks in which Willman and Bolt ties: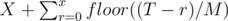

Note that . That means that floor((T - r) / M) = v for exactly M values of r.

We can count the number of values of r in which floor((T - r) / M) = floor((T - 0) / M) = v₁, and the values of r in which floor((T - r) / M) = floor((T - X) / M) = v₂. Each of the remaining values v₁ - 1, v₁ - 2, ..., v₂ + 1 will appear exactly M times.

Problem D. Super M

Observation 1: Ari should teleport to one of the attacked cities (it doesn't worth going to a city that is not attacked since then she should go to one of the attacked cities)

Observation 2: The nodes visited by Ari will determine a sub-tree T of the original tree, this tree is unique and is determined by all the paths from two attacked cities.

Observation 3: If Ari had to return to the city from where she started, then the total distance would be 2e, where e is the number of edges of T, that is because she goes through each edge forward and backward

Observation 4: If Ari does not have to return to the starting city (the root of T), then the total distance is 2e - L, where L is the distance of the farthest node from the root

Observation 5: In order to get a minimum total distance, Ari should chose one diameter of the tree, and teleport to one of its leaves.

The problem is now transformed in finding the diameter of a tree that contains the smallest index for one of its leaves. Note that all diameters pass through the center of the tree, so we can find all the farthest nodes from the center...and [details omitted].

Problem E. BCPC

Let’s represent the reading and writing speeds of the students as points in a plane. Two students i, j are compatible if ri'·wj' - rj'·wi' > 0 this equation is identical to the cross product: (ri', wi') × (rj', wj′) > 0. Using this fact is easy to see that three students i, j, k are compatible if the triangle (r_i, w_i), (r_j, w_j), (r_k, w_k) contains the point (x, y). So the problem is reduced to count the number of triangles that contains the origin.

Let’s count the triangles that have two known vertices i and j (look at the picture above). It is easy to see that the third vertex should be inside the region S. So now we have to be able of counting points that are between two rays, that can be done using binary search (ordering the points first by slope and then by the distance to the origin).

Now given a point i, let’s count the triangles that have i as a vertex (look at the picture above again). We have to count the points that lie between the ray iO, and every other ray jO (the angle between iO and jO must be  ≤ 180).

Let S_j denote the number points that are between the rays OR and jO, then the number of triangles that have i as a vertex are 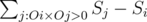. This summation can be calculated if we pre-calculate the cumulative sums of S_j. The overall complexity is O(n·logn).