Hints:
div2A: Try conversions between bases.
div2B: Solve a simpler version of the problem where Ai + 1 ≠ Ai for all i.
div1A: What are the shortest paths of the vehicles? what's the shorter of those paths?
div1B: Forget about the ceiling function. Draw points (i, A[i]) and lines between them — what's the Lipschitz constant geometrically?
div1C: Some dynamic programming. Definitely not for the exp. score of one person — look at fixed scores instead.
div1D: Compute dif(v) in O(N) (without hashing) and then solve the problem in O(N2). Read my editorial of TREEPATH from Codechef.
div1E: Can you solve the problem without events of type 1 or 2? Also, how about solving it offline — as queries on subsets.
What, you thought I'd post solutions? Nope. Read the hints, maybe they'll help you. The solutions will appear here gradually.
Div. 2 A: The Two Routes
It's easy to compare two numbers if the same base belong to both. And our numbers can be converted to a common base — just use the formulas
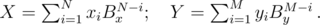
A straightforward implementation takes O(N + M) time and memory. Watch out, you need 64-bit integers! And don't use pow — iterating 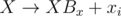 is better.
is better.
Div. 2 C / Div. 1 A: The Two Routes
The condition that the train and bus can't meet at one vertex except the final one is just trolling. If there's a railway  , then the train can take it and wait in town N. If there's no such railway, then there's a road
, then the train can take it and wait in town N. If there's no such railway, then there's a road  , the bus can take it and wait in N instead. There's nothing forbidding this :D.
, the bus can take it and wait in N instead. There's nothing forbidding this :D.
The route of one vehicle is clear. How about the other one? Well, it can move as it wants, so the answer is the length of its shortest path from 1 to N... or - 1 if no such path exists. It can be found by BFS in time O(N + M) = O(N2).
In order to avoid casework, we can just compute the answer as the maximum of the train's and the bus's shortest distance from 1 to N. That way, we compute 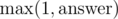 ; since the answer is ≥ 1, it works well.
; since the answer is ≥ 1, it works well.
In summary, time and memory complexity: O(N2).
Bonus: Assume that there are M1 roads and M2 railways given on the input, all of them pairwise distinct.
Bonus 2: Additionally, assume that the edges are weighted. The speed of both vehicles is still the same — traversing an edge of length l takes l hours.






