Let's fix the number a of strings of length p and the number b of strings of length q. If a·p + b·q = n, we can build the answer by splitting the string s to a parts of length p and b parts of length q, in order from left to right. If we can't find any good pair a, b then the answer doesn't exist. Of course this problem can be solved in linear time, but the constraints are small, so you don't need linear solution.
Complexity: O(n2).
612B - HDD is Outdated Technology
You are given the permutation f. Let's build another permutation p in the following way: pfi = i. So the permutation p defines the number of sector by the number of fragment. The permutation p is called inverse permutation to f and denoted f - 1. Now the answer to problem is 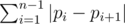 .
.
Complexity: O(n).
612C - Replace To Make Regular Bracket Sequence
If we forget about bracket kinds the string s should be RBS, otherwise answer doesn't exist. If the answer exists for each opening bracket matches to exactly one closing bracket and vice verse. Easy to see that if two matching brackets have the same kind we don't need to replace them. In other case we can change the kind of closing bracket to the kind of opening. So we can build some answer. Obviously the answer is minimal, because the problems for some pair of matching pairs are independent and can be solved separately.
The only technical problem is to find the matching pairs. To do that we should store the stack of opening brackets. Let's iterate from left to right in s and if the bracket is opening, we should simply add it to stack. Now if the bracket is closing there are three cases: 1) the stack is empty; 2) at the top of the stack is the opening bracket with the same kind as the current closing; 3) the kind of the opening bracket differs from the kind of the closing bracket. In the first case answer doesn't exist, in the second case we should simply remove the opening bracket from the stack and in the third case we should remove the opening bracket from the stack and increase the answer by one.
Complexity: O(n).
612D - The Union of k-Segments







