616A - Сравнение длинных чисел

Note that solutions in Java with BigInteger class or input() function in Python2 will fail in this problem. The reason is the next: standard objects stores numbers not in decimal system and need a lot of time to convert numbers from decimal system. Actually they are working in O(n²), where n is the legth of the number.

To solve this problem you should simply read the numbers to strings and add leading zeroes to the shorter one until the numbers will be of the same length. After that you should simply compare them alphabetically.

С++ solution

Python solution

Complexity: O(n).

616B - Ужин с Наташей

Firstly you should find the minimum value in each row and after that you should find the maximum value over that minimums. It's corresponding to the strategy of Jack and Emma.

C++ solution

Complexity: O(nm).

616C - Лабиринт

Let's enumerate all the connected components, store their sizes and for each empty cell store the number of it's component. It can be done with a single dfs. Now the answer for some impassable cell is equal to one plus the sizes of all different adjacent connected components. Adjacent means the components of cells adjacent to the current impassable cell (in general case each unpassable cell has four adjacent cells).

C++ solution

Complexity: O(nm).

616D - Наидлиннейший k-хороший подотрезок

This problem is given because on the Codeforces pages we often see questions like "What is the method of the two pointers?". This problem is a typical problem that can be solved using two pointers technique.

Let's find for each left end l the maximal right end r that (l, r) is a k-good segment. Note if (l, r) is a k-good segment then (l + 1, r) is also a k-good segment. So the search of the maximal right end for l + 1 we can start from the maximal right end for l. The only thing that we should do is to maintain in the array cnt_x for each number x the number of it's occurrences in the current segment (l, r) and the number of different numbers in (l, r). We should move the right end until the segment became bad and then move the left end. Each of the ends l, r will be moved exactly n times.

C++ solution

Complexity: O(n).

616E - Сумма остатков

Unfortunately my solution for this problem had overflow bug. It was fixed on contest. Even so I hope you enjoyed the problem because I think it's very interesting.

Let's transform the sum 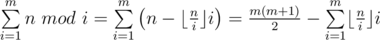. Note that the last sum can be accumulated to only value min(n, m), because for i > n all the values will be equal to 0.

Note in the last sum eithe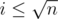r or . Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all 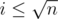. We will accumulate the second sum independently for all different values 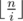. Firstly we should determine for which values i we will have the value 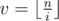. Easy to see that for the values i from the interval 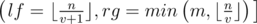. Also we can note that the sum of the second factors in 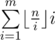with fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression . So we have solution with complexity .

С++ solution

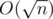Complexity: 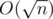.