Introduction
Mo's Algorithm has become pretty popular in the past few years and is now considered as a pretty standard technique in the world of Competitive Programming. This blog will describe a method to generalize Mo's algorithm to maintain information about paths between nodes in a tree.
Prerequisites
Mo's Algorithm — If you do not know this yet, read this amazing article before continuing with this blog.
Euler Tour or DFS Order of the Tree.
Problem 1 — Handling Subtree Queries
Consider the following problem. You will be given a rooted Tree T of N nodes where each node is associated with a value A[node]. You need to handle Q queries, each comprising one integer u. In each query you must report the number of distinct values in the subtree rooted at u. In other words, if you store all the values in the subtree rooted at u in a set, what would be the size of this set?
Constraints
1 ≤ N, Q ≤ 105
1 ≤ A[node] ≤ 109
Solution(s)
Seems pretty simple, doesn't it? One easy way to solve this is to flatten the tree into an array by doing a Preorder traversal and then implement Mo's Algorithm. Maintain a lookup table which maintains the frequency of each value in the current window. By maintaining this, the answer can be updated easily. The complexity of this algorithm would be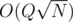 
Note that you can also solve this in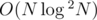 
by maintaining a set in each node and merging the smaller set into the larger ones.
Problem 2 — Handling Path Queries
Now let's modify Problem 1 a little. Instead of computing the number of distinct values in a subtree, compute the number of distinct values in the unique path from u to v. I recommend you to pause here and try solving the problem for a while. The constraints of this problem are the same as Problem 1.
The Issue
An important reason why Problem (1) worked beautifully was because the dfs-order traversal made it possible to represent any subtree as a contiguous range in an array. Thus the problem was reduced to "finding number of distinct values in a subarray [L, R] of A[]. Note that it is not possible to do so for path queries, as nodes which are O(N) distance apart in the tree might be O(1) distance apart in the flattened tree (represented by Array A[].). So doing a normal dfs-order would not work out.
Observation(s)
Let a node u have k children. Let us number them as v1,v2...vk. Let S(u) denote the subtree rooted at u.
Let us assume that dfs() will visit u's children in the order v1,v2...vk. Let x be any node in S(vi) and y be any node in S(vj) and let i < j. Notice that dfs(y) will be called only after dfs(x) has been completed and S(x) has been explored. Thus, before we call dfs(y), we would have entered and exited S(x). We will exploit this seemingly obvious property of dfs() to modify our existing algorithm and try to represent each query as a contiguous range in a flattened array.
Modified DFS-Order
Let us modify the dfs order as follows. For each node u, maintain the Start and End time of S(u). Let's call them ST(u) and EN(u). The only change you need to make is that you must increment the global timekeeping variable even when you finish traversing some subtree (EN(u) = ++cur). In short, we will maintain 2 values for each node u. One will denote the time when you entered S(u) and the other would denote the time when you exited S(u). Thus, ST() and EN() will have no values in common. Consider the following tree. Given below are the ST() and EN() values of the nodes.
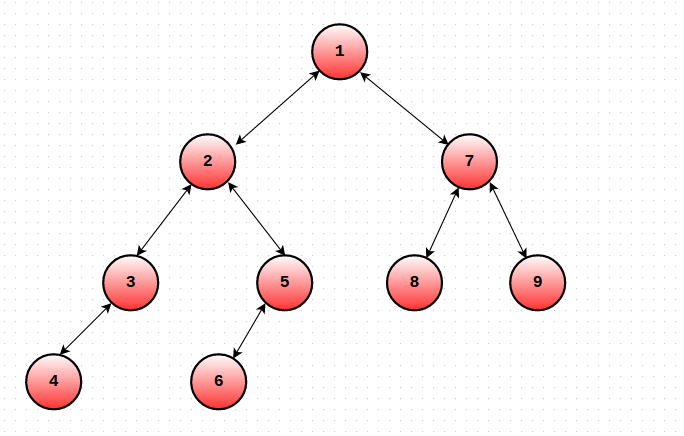ST(1) = 1 EN(1) = 18
ST(2) = 2 EN(2) = 11
ST(3) = 3 EN(3) = 6
ST(4) = 4 EN(4) = 5
ST(5) = 7 EN(5) = 10
ST(6) = 8 EN(6) = 9
ST(7) = 12 EN(7) = 17
ST(8) = 13 EN(8) = 14
ST(9) = 15 EN(9) = 16
The Algorithm
Now that we're equipped with the necessary weapons, let's understand how to process the queries. Let a query be (u, v). We will try to map each query to a range in the flattened array. Let L(u) ≤ L(v) where L(u) denotes level of node u in T. Let P = LCA(u, v) denote the lowest common ancestor of nodes u and v. There are 2 possible cases:
Case 1: P = u
In this case, our query range would be [ST(u), ST(v)]. Why will this work?
Consider any node x that does not lie in the (u, v) path. Notice that x occurs twice or zero times in our specified query range. Therefore, the nodes which occur exactly once in this range are precisely those that are on the (u, v) path! This forms the crux of our algorithm. Thus, while implementing Mo's, our add/remove function needs to check the number of times a particular node appears in a range. If it occurs twice (or zero times), then we don't take it's value into account! This can be easily implemented while moving the left and right pointers.
Case 2: P ≠ u
In this case, our query range would be [EN(u), ST(v)] + [ST(P), ST(P)].
The same logic as Case 1 applies here as well. The only difference is that we need to consider the value of P i.e the LCA separately, as it would not be counted in the query range.
This same problem is available on SPOJ.
If you aren't sure about some elements of this algorithm, take a look at this neat code.
Conclusion
We have effectively managed to reduce problem (2) to number of distinct values in a subarray by doing some careful bookkeeping. Now we can solve the problem in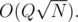 
This modified DFS order works brilliantly to handle any type path queries and works well with Mo's algo. We can use a similar approach to solve many types of path query problems.
For example, consider the question of finding number of inversions in a (u, v) path in a Tree T, where each node has a value associated with it. This can now be solved in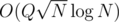 
by using the above technique and maintaining a BIT or Segment Tree.
This is my first blog and I apologize for any mistakes that I may have made. Thanks a lot for reading!
