Lets solve the problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:
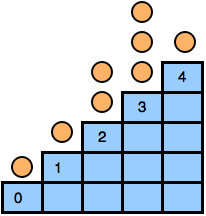
Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change,
if A move a coin from an odd step to an even step, the logic above won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.






