Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:
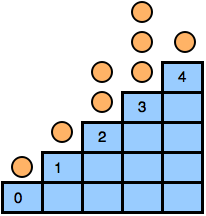
Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.
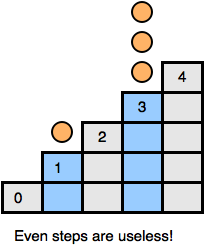
Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
In the HackerRank problem, there is a tree where each node contains zero or more coins.
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
In the HackerRank problem, there is a tree where each node contains zero or more coins.
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
Lets solve move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. I am not going to discuss the detailed approach, I will only discuss how to solve the initial game with any queries because that is the hardest part.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you to first learn about it.
In Staircase nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:

Two players play in turns. In his/her move a player can chose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps and even steps. Now lets think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from a even step, I will move those nodes again to another even step and will still remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps counts. If you take one or more coin from a odd step and move them to a even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in a odd-step as a pile of stones in a standard nim game.

Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
In the HackerRank problem, there is a tree and each node can contain zero or more coins.
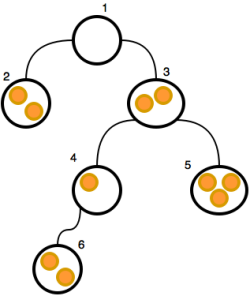
In each move, a player can move one or more coin from a node (which is not the root) to its parent node. If a player can't make a move, he/she loses the game.
This is same as Staircase nim, but on a tree. You just need to calculate the distance between each node and the root.






